Area Of Colored Squares
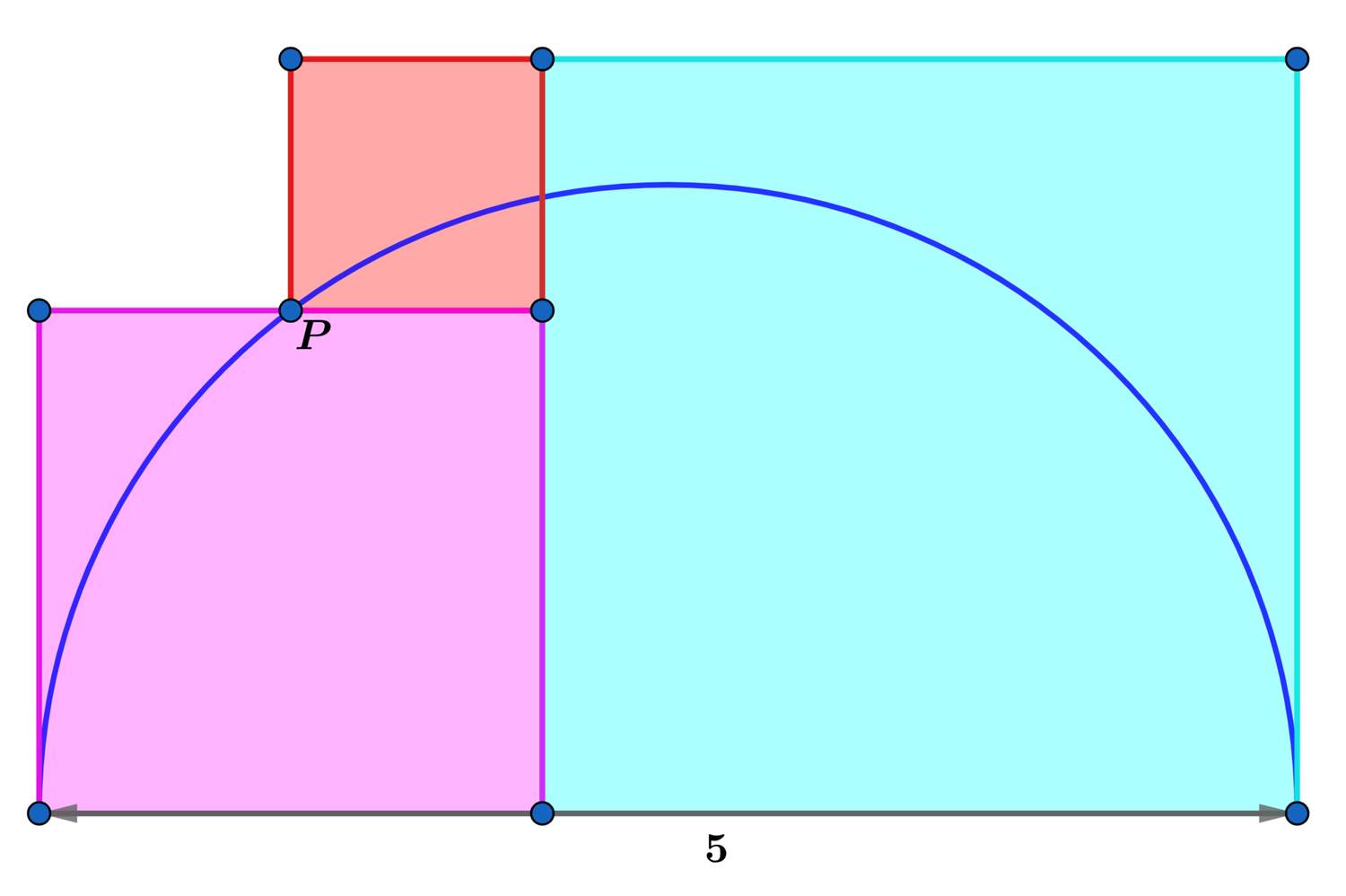
In the three colored squares above, the semicircle with diameter 5 passes through the vertex of the red square at point P .
Find the total area of the three colored squares.
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
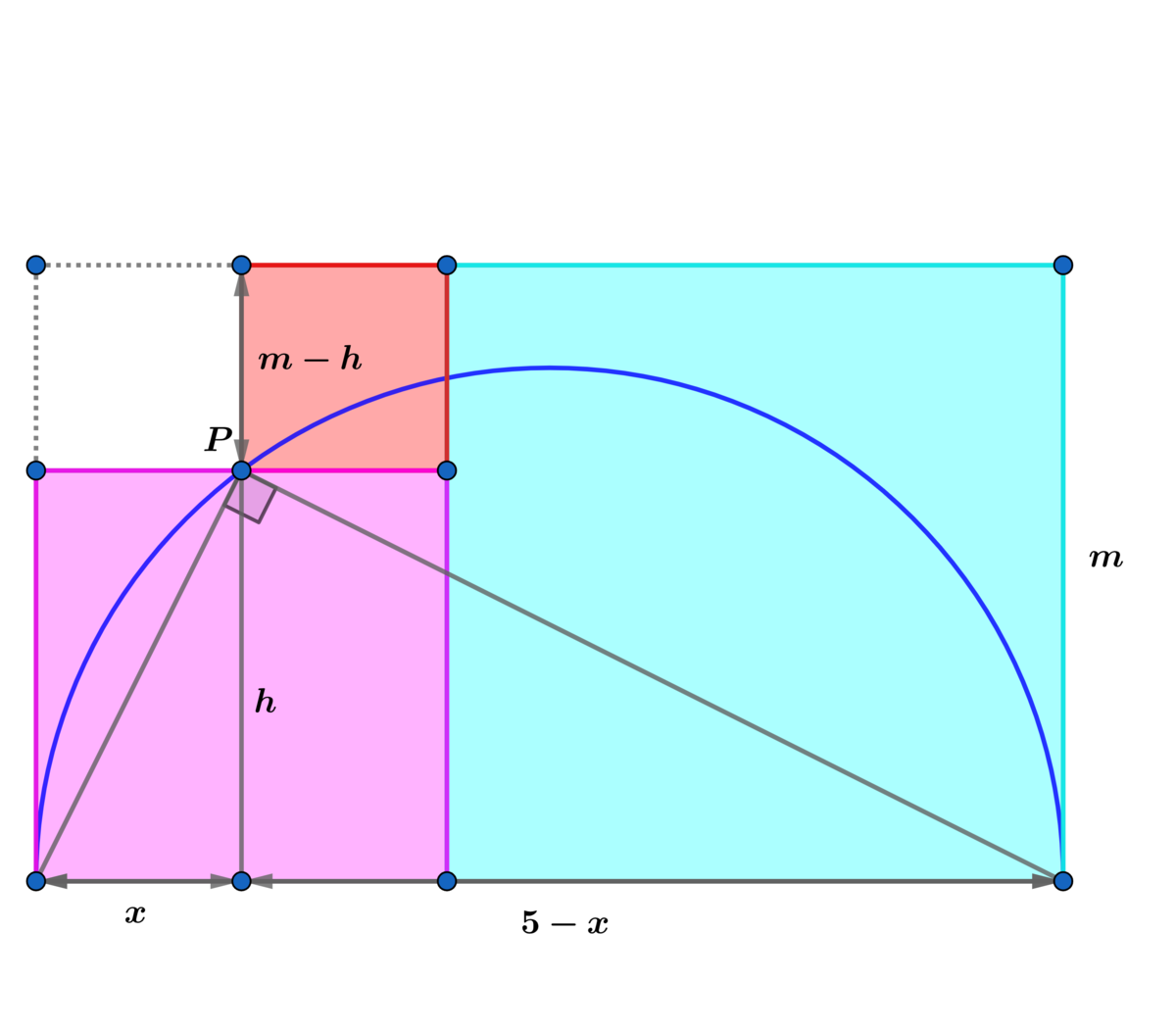
h 2 = x ( 5 − x ) ⟹ h = x ( 5 − x )
m = 5 − h ⟹ m − h = 5 − 2 h
A p i n k = h 2
A l i g h t b l u e = m 2 = ( 5 − h ) 2
A r e d = ( m − h ) 2 = ( 5 − 2 h ) 2
A w h i t e = x ( m − h ) = x ( 5 − 2 h )
⟹ 5 m = 5 ( 5 − h ) = h 2 + 2 5 − 1 0 h + h 2 + 2 5 − 2 0 h + 4 h 2 + 5 x − 2 x h ⟹
6 h 2 + 5 x + 2 5 = ( 2 x + 2 5 ) h
Using h = x ( 5 − x ) ⟹
− 6 x 2 + 3 5 x + 2 5 = ( 2 x + 2 5 ) x ( 5 − x )
Squaring both sides and simplifying we obtain:
8 x 4 − 6 8 x 3 + 2 1 0 x 2 − 2 7 5 x + 1 2 5 = 0
By inspection x = 1 is a root to the above equation and dividing 8 x 4 − 6 8 x 3 + 2 1 0 x 2 − 2 7 5 x + 1 2 5 by x − 1 we have:
( x − 1 ) ( 8 x 3 − 6 0 x 2 + 1 5 0 x − 1 2 5 ) = 0 ⟹ ( x − 1 ) ( 2 x − 5 ) 3 = 0
⟹ x = 1 , x = 2 5
x = 1 ⟹ h = 2 ⟹ m = 3 ⟹ m − h = 1
x = 2 5 ⟹ h = 2 5 ⟹ m = 2 5 ⟹ m − h = 0
∴ drop x = 2 5 and pick x = 1
∴ the desired area A = 2 2 + 3 2 + 1 = 1 4 .
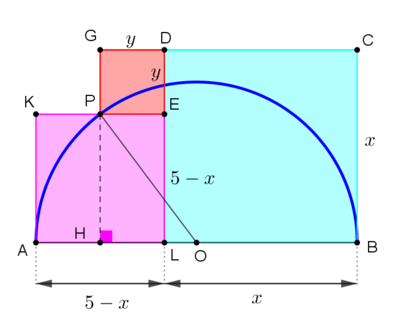 Drop
P
H
perpendicular to the diameter
A
B
.
Drop
P
H
perpendicular to the diameter
A
B
.
Denote by
x
and
y
the side lengths of the light blue and red squares respectively and by
O
the center of the semicircle.
Then,
E
L
=
P
H
=
A
L
=
5
−
x
.
Moreover,
D
E
+
E
L
=
D
L
⇒
y
+
(
5
−
x
)
=
x
⇒
y
=
2
x
−
5
Since,
y
>
0
we also have
2
x
−
5
>
0
⇔
x
>
2
5
.
By Pythagoras’ theorem on the right-angled
△
O
P
H
,
P
H
2
+
H
O
2
=
P
O
2
⇒
(
5
−
x
)
2
+
(
y
+
x
−
2
5
)
2
=
(
2
5
)
2
⇔
(
1
)
(
5
−
x
)
2
+
(
2
x
−
5
+
x
−
2
5
)
2
=
4
2
5
⇔
2
x
2
−
1
1
x
+
1
5
=
0
⇔
x
=
2
5
or
x
=
3
Due to the restriction, the value
2
5
is rejected. Hence
x
=
3
and this gives
y
=
1
.
Thus, the total area of the three squares is
A
=
x
2
+
y
2
+
(
5
−
x
)
2
=
3
2
+
1
2
+
2
2
=
1
4
.
We have squares of three colors: pink, red, and cyan. Let's refer to the side lengths of each square as side lengths p (pink square), r (red square), and c (cyan square).
The following statements are what we know to be true about the figure, where the x and y values refer to the horizontal and vertical side lengths, respectively.
x p + x c = 5
x r = 2 1 x p
y p + y r = y c
We know, though, that the x and y side lengths for each respective colored square are equal. So we can now refer to, for example, x p and y p , as just p .
With this being true, the equations above can be written as:
(1) … p + c = 5
(2) … r = 2 1 p → 2 r = p
(3) … p + r = c
These are much simpler to substitute into one another to solve for variables.
Solving equations (1), (2), and (3) for variables
Let's use (2) to solve (3) for c :
2 r + r = c → c = 3 r
Now that we know that c = 3 r and p = 2 r , we can solve (1) in terms of r .
2 r + 3 r = 5
→ 5 r = 5
→ r = 1
So, now that we know that r = 1 , we also know that:
From (3), where p = 2 r , 2(1) + (1) = c)
→ c = 3
p + 3 = 5 → p = 2
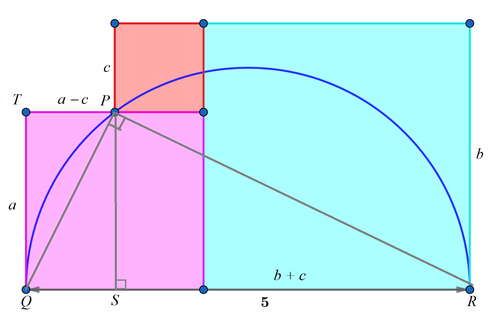
Let the side lengths of the purple, blue, and red squares be a , b , and c . We note that because Q R is a diameter, ∠ Q P R = 9 0 ∘ . Then
P R 2 + P Q 2 T P 2 + T Q 2 + P S 2 + S R 2 ( a − c ) 2 + a 2 + a 2 + ( c + b ) 2 ( 3 a − 5 ) 2 + a 2 + a 2 + ( 1 0 − 3 a ) 2 9 a 2 − 3 0 a + 2 5 + 2 a 2 + 9 a 2 − 6 0 a + 1 0 0 2 0 a 2 − 9 0 a + 1 0 0 2 a 2 − 9 a + 1 0 ( 2 a − 5 ) ( a − 2 ) ⟹ a = Q R 2 = 2 5 = 2 5 = 2 5 = 2 5 = 0 = 0 = 0 = 2 Note that b = 5 − a and a + c = b ⟹ c = 5 − 2 a Since a < 2 . 5
Therefore b = 5 − a = 3 and c = 5 − 2 a = 1 and the area of the three squares is 1 2 + 2 2 + 3 2 = 1 4
Let red be x, purple be y and blue be z size squares. Easy to show,
z=x+y, z+y=5 and y/(y-x)=(z+y-x)/y
Therefore, x=1, y=2 and z=3, giving answer as 14.
Let B = length of the side of the blue square, R = length of a side of the red square, and P = length of the side of the purple square. From the picture, we find:
B + P = 5
P + R = B
P + (P-R) = B
This gives three equations in three unknowns. Solving yields R = 1, B = 3, and P = 2. Hence, the sum of the areas is:
1^2 + 2^2 + 3^2 = 14
How did you get the third equation?
Hi Thanos - Refer to the picture in Rocco Dalto's solution. The length of the side of the white square is P - R. The length of the purple square (P) plus the length of the white square (P - R) is the length of the blue square (B) - i.e., P + (P-R) = B
Log in to reply
Hi Ron! I think there is still something missing: How do we know that the white rectangle is a square?
Hi Thanos - You make a good point. I was largely assuming it as "obvious from the picture", which (of course) can lead to faulty conclusions. However, we can prove it as follows. By the way, I realize I called the length of the purple square "P", which was used as a point in the problem. In what follows, P is the length of the purple square.
Choose a coordinate system with the center of the semicircle at the origin. The radius of the circle is given as 2.5. Let x be defined as the distance between the origin and the lower right hand corner of the purple square. Then, recognizing that the points that points (B-x,0), (-x-P, 0), and (-x-R, P) all lie on the circle, the following equations must be satisfied:
P + x + B = 5
(x+R)^2 + P^2 = 2.5^2
(B-x)^2 = 2.5^2
(-x-P)^2 = 2.5^2
Solving these equations gives the desired result.
Log in to reply
Ok now. I don't think one could avoid using Pythagoras' theorem in a way or an other:)
Log in to reply
I did by using similar triangles instead :-)
Log in to reply
@David Vreken – Well done David! Anyway, I was wrong, since Pythagoras' theorem can be proved by the similarity of △ P Q R , △ R P S and △ R Q P (as labeled in your figure).
Sorry, the first equation should read x + P = 2.5, not x+P + B = 5. Not sure how to edit a comment...
I think you’re right. In response to your question “How did I know it is a square?”, the answer is “I got lucky”. Better to be lucky than good sometimes. Thanks for your input
You wellcome!
Let the red square have a side length of x and the purple square have a side length of y , so that the blue square has a side length of x + y , and label the diagram as follows:
Since Q R is a diameter, ∠ Q P R is a right angle, and △ Q S P ∼ △ P S R by AA similarity.
This means that P S Q S = S R P S , or y y − x = y + 2 x y , which simplifies to y = 2 x for x = 0 .
Also, Q R = Q T + T R = y + ( x + y ) = x + 2 y = 5 .
The two equations y = 2 x and x + 2 y = 5 solve to x = 1 and y = 2 .
Therefore, the three squares have side lengths of 1 , 2 , and 1 + 2 = 3 , and the sum of their areas is 1 2 + 2 2 + 3 2 = 1 4 .