Semi Semi Circles
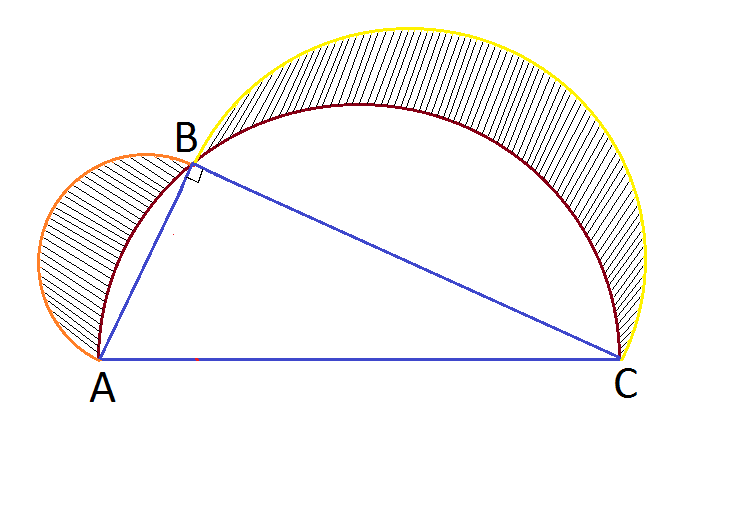 In the figure above, semicircles are constructed on the hypotenuse and legs of a right angle triangle. If
S
1
,
S
2
are the area of shaded regions and
S
is the area of right angled triangle, which of the following is true ?
In the figure above, semicircles are constructed on the hypotenuse and legs of a right angle triangle. If
S
1
,
S
2
are the area of shaded regions and
S
is the area of right angled triangle, which of the following is true ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed

Nice one both the problem n solution
why you have taken S in the RHS. i dont understand pls clarify
Area of shaded region ( S 1 + S 2 ) = Total area ( Area of semicircles on legs AB & BC + Area of triangle ) - Area of semicircle on hypotenuse AC
But Area of triangle is covered in area of semicircle on hypotenuse AC
@Sanjay Singh – Please figure this out : You have two ways to calculate total area, 1.Total area = S1 + S2 + Semicircle AC. 2.Total area = Triangle S + Semicircle AB + Semicircle BC. So, S1 + S2 + Semicircle AC = Triangle S + Semicircle AB + Semicircle BC. Then, S1 + S2 = Triangle S + Semicircle AB + Semicircle BC - Semicircle AC. Because AB^2+BC^2-AC^2=0 (Pythagorean), we get : S1 + S2 = Triangle S
Thank u for your solution
Assume the radius of two circles is r and R respectively. According to Pythagoras theory to get the results: S 1 + S 2 = 2 π ∗ ( r 2 + R 2 ) − ( 2 π ∗ ( r 2 + R 2 ) − 2 1 ∗ ( r R ) ) = S So: S 1 + S 2 = S
correct relationship is S1 + S2 = S Now S = (L * B )/2 Now S1 + S2 = Area of semi circle on AB as diameter + Area of semi circle on BC as diameter - (Area of semi circle on AC as diameter - Area of right triangle) = (pi/4)* B^2 + (pi/4) L^2 - ( Pi/4) ( B^2 + L^2) + ( L B)/2 = (L*B) / 2 = S Hence Proved
A nice short solution. You may simply add, " s e c o n d " r 2 + R 2 = A C 2
ABsegment + BCsegment = AsemicircleAC - S
S1 + S2 = AsemicircleAB + AsemicircleBC - AsemicircleAC + S
= PiAB²/8 + PiBC²/8 - PiAC²/8 + S , AC² = BC² + AB² then
= (PiAB² + PiBC² - Pi(BC² + AB²)) / 8 + S
= 0 + S
S1 + S2 = S
S1 + S2 = Pi(AB^2/4) + Pi(BC^2/4) - {Pi(AC^2/4) - S}
S1 + S2 = Pi/4(AB^2 + BC^2) - {Pi(AC^2/4) - S}
S1 + S2 = Pi/4(AC^2) - {Pi(AC^2/4) - S}
S1 + S2 = S
Let AB = 2 x and BC = 2 y , so by pythagoras' theorem AC = 2R = 2 x 2 + y 2 ⇒ R = x 2 + y 2 so area of large semicircle = 2 π ( x 2 + y 2 ) . Now we take the difference of these area to calculate the area of sectors AB and BC (lets call this A):
A = 2 π ( x 2 + y 2 ) - 2 x y (#1). Now area of semi-circle BC = 2 π y 2 and area of semi-circle AB = 2 π x 2 , so their sum is 2 π ( x 2 + y 2 ) ⇒ \S 1 + \S 2 = 2 π ( x 2 + y 2 ) - [ 2 π ( x 2 + y 2 ) - 2 x y ]= 2 x y (from #1).
∴ \S 1 + \S 2 = S
Typos:-BC =2. y . Also add AC=R. You may use S 1 , S 2 .
Area of semicircles is directly proportional with its diameter squared
Area of semicircle with diameter AB + area of semicircle with diameter BC = area of semicircle with diameter AC (pythagorean theorem)
Subtracting the non-dashed parts around triangle ABC from the equation we are left with S1+S2 = area of triangle