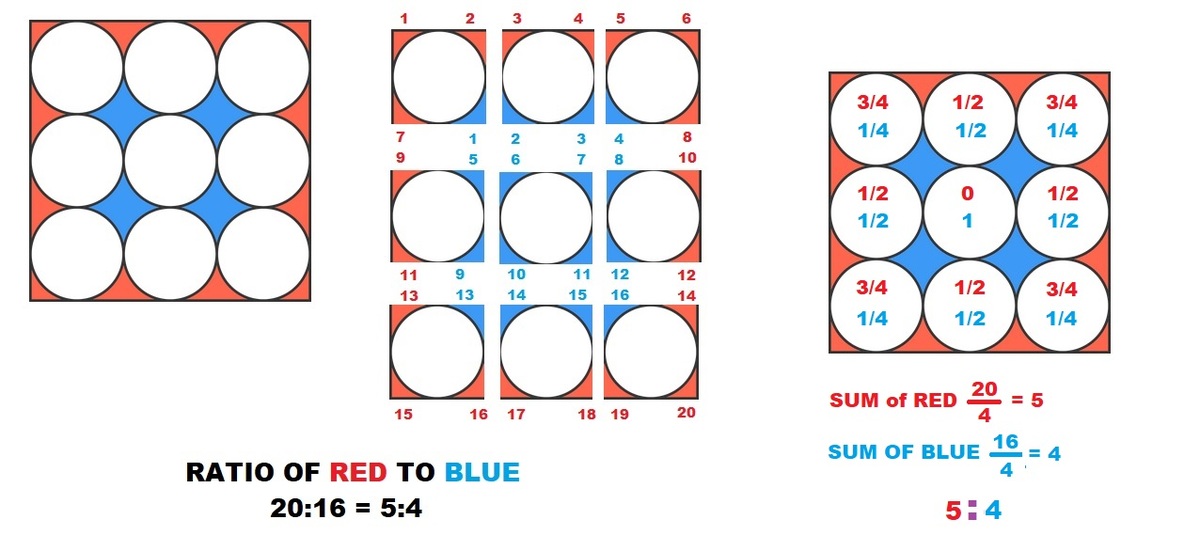
Area problem - 3
Nine identical circles are symmetrically fitted into a square, as shown.
What is the ratio of the red area to blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Excellent solution - illustrating my precise thought processes.
How do you know the red area = blue area
Log in to reply
In my solution, the red area is not equal to the blue area.
Log in to reply
No the individual arcs..
Log in to reply
@Aman Thegreat – Yes they are equal, you can observe that if you inscribed a circle in a square. It is because of symmetry.
Log in to reply
@A Former Brilliant Member – Yes, that is an intuition . But can you perhaps prove it more rigorously?
Because if you circumscribe a circle in a square, you'll notice if you rotate 90 degrees, it is exactly the same, hence the corners have the exact same shape and area
Log in to reply
How can you prove it geometrically?
Log in to reply
@Aman Thegreat – If you circumscribed a circle in a square, the point of contact is the midpoint of every edges of the square
Log in to reply
@Ong Zi Qian – What is the Proof for that..
Log in to reply
@Aman Thegreat – Obviously the diameter of the circle is equal to the edge of square. (Or we can say that the radius of circle is half of the edge of square.)
Therefore, if the circle is circumscribed in a square, the point of contact is the midpoint of every edges of the square.
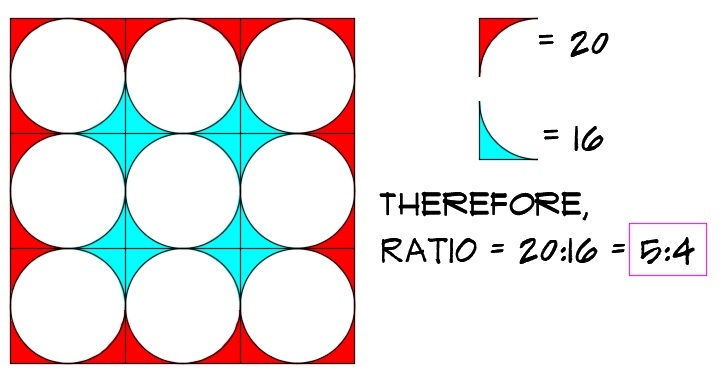
We know that all the star-shaped pieces are congruent, and the red pieces are blue pieces either split in half or into a quarter. We can combine the right and left red pieces and the top and bottom red pieces, leaving us with 4 star-shapes. The 4 corner red pieces form one last star-shape, leaving us with 5 red star-shapes to 4 blue star-shapes.
I had the same thought processes.
Please accept my sincere apologies; My eyes read the choice as 5.4. Ed Gray
An easy solution to this, Assume radius of the circle is r. Area of the blue region can be found out by considering a square joining the centres of all the circles. Area of the red region can be found out by subtracting all the circles area+area of the blue region from the area of the bigger square. From calculations we find that area of blue is 16-4 pie r^2. and area of red is 20-5 pie r^2 . their ratio is 5:4 .
π is spelled Pi not Pie, HAHA it confused me a little
Very clear explanation
If you count the decimal percentage of the circles inside blue and red respectively, ex. 0.5+0.5+0.5+0.5+0.25+0.25+0.25+0.25+1=4 for the blue circles, and the same pattern for the red circles, you get the same ratio to the colored sections, as the area covered by the circles, in this instance at least, is in the same accordance to the area covered by the non circle section. This gives you a ratio of circles red to blue equal to 5:4, this the same for colored sections.
Let’s denote the constant radius of these circles r . From the scale of the diagram, we can tell the following: Sidelength S 1 of the blue square is equal to r + 2 r + r = 4 r so A r e a ( B l u e ) = ( 4 r ) 2 = 1 6 r 2 .
We can also see from the diagram that the sidelength S 2 of the larger square is equal to 3 × 2 r = 6 r , meaning the total area A r e a ( B l u e ) + A r e a ( R e d ) = ( 6 r ) 2 = 3 6 r 2 . Now, we can solve 3 6 r 2 − 1 6 r 2 = 2 0 r 2 = A r e a ( R e d ) .
Finally, the fun part! 1 6 r 2 2 0 r 2 = 4 5 ! ! !
Note: The 2 squares (Blue Square & Larger Square) are squares, we can tell using the fact that the circles are given CONGRUENT AND SYMMETRICAL. Always try your best to avoid interpreting a problem with the assumption of an accurate diagram.