Area Problem 5
 Let
A
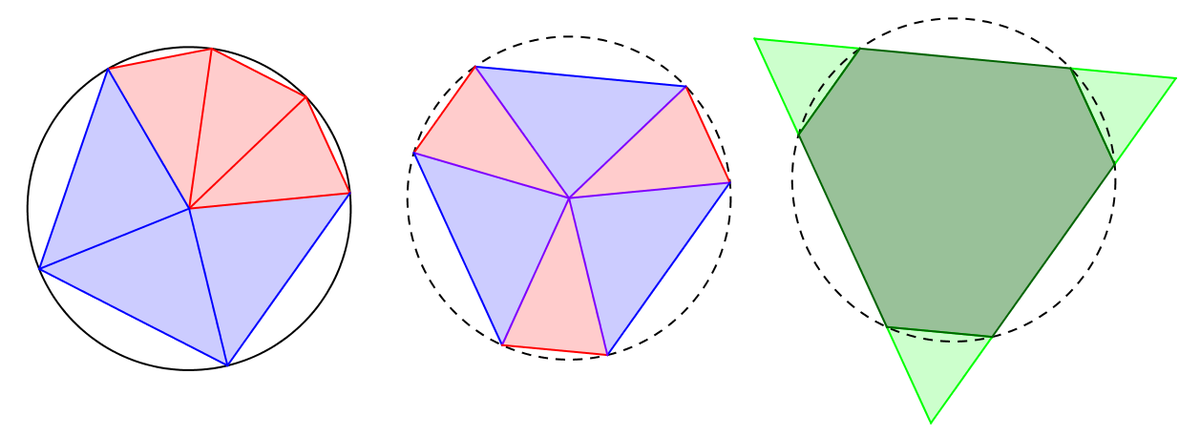
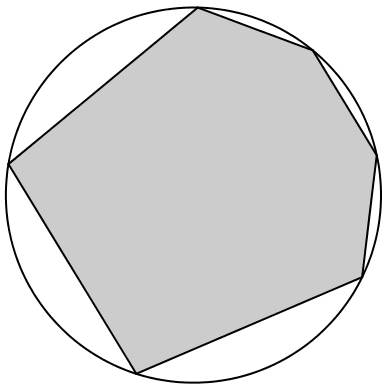
be the area of the cyclic hexagon, whose side lengths are 2,2,2,4,4, and 4, as shown. Find
A
2
.
Let
A
be the area of the cyclic hexagon, whose side lengths are 2,2,2,4,4, and 4, as shown. Find
A
2
.
Bonus: Solve without trig functions.
The answer is 507.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Glad to see you back sir!
sir can you please solve this: https://brilliant.org/problems/confusing-question-no-way-out/
That's a beautiful solution!
Very elegant. I had thought at first that this still requires a trigonometry function but it can be completed using the following formula for the area of a triangle
Sqrt [s (s-a) (s-b)*(s-c)]
Where a,b,c are the side lengths and s is half the perimeter.
Log in to reply
alternatively, altitude of equilateral (or isosceles) bisects the base, find altitude with Pythagoras theorem.
Log in to reply
Ah yes. Much simpler
Log in to reply
@Malcolm Rich – Simpler still: you can tile the dark green shaded area with the light green triangles! (Thirteen of them, to be exact)
Log in to reply
@Chris Lewis – true, although the area of small triangle still must be found.
What the heck, this is so elegant, compared to my solution!! A regular triangle with side s has area 4 1 3 s 2 so that A 2 = ( ( 8 2 − 3 × 2 2 ) × 4 1 × 3 ) 2 = 1 3 2 × 3 = 5 0 7
that is true
That is so clean!! I doubt whether the problem was intended for the brilliant solution and not the other way around
Going for the bonus
If we draw radii from the vertices to the centre, we get three identical isosceles triangles with sides R, R, 2, and three identical isosceles triangles with sides R, R, 4.
We therefore know that the angles at the centre of two different triangles add up to 120°.
To find out the individual angles, we start out with a unit circle centred at the origin, and choose points A = ( 1 , 0 ) , B = ( − 2 1 , 2 3 ) , so that they are 120° apart. We are looking for some point P = ( x , y ) on the unit circle having d ( P , B ) = 2 d ( P , A )
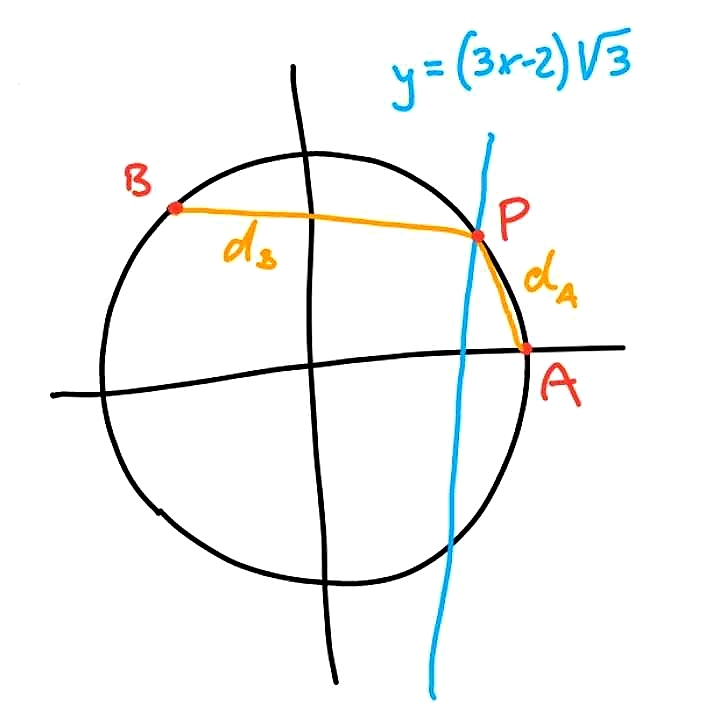
For shortness set d A = d ( P , A ) and d B = d ( P , B ) . We have
x 2 + y 2 = 1
d A 2 = ( x − 1 ) 2 + ( y − 0 ) 2 = x 2 − 2 x + 1 + y 2 = 2 − 2 x
d B 2 = ( x + 2 1 ) 2 + ( y − 2 3 ) 2 = x 2 + x + y 2 − 3 y + 1 = 2 + x − 3 y
d B = 2 d A ⇒ 2 + x − 3 y = 4 ( 2 − 2 x ) ⇒ 9 x − 3 y = 6 ⇒ y = ( 3 x − 2 ) 3
So our point P lies on the line y = 3 3 x − 2 3
Plugging this expression for y into x 2 + y 2 − 1 = 0 gives the equation 2 8 x 2 − 3 6 x + 1 1 = 0 .
which solves to x = 2 × 2 8 3 6 ± 3 6 2 − 4 × 2 8 × 1 1 = 1 4 1 1 . (The diagram above makes it clear that we should take the largest root.) Thus we find P = ( x , y ) = ( 1 4 1 1 , 1 4 5 3 )
Now that we have found P , we can calculate the triangular areas, which is done easiest using cross products: A 1 = 2 1 ∣ ( P × A ) ∣ = 2 8 5 3 and A 2 = 2 1 ∣ ( P × B ) ∣ = 7 2 3 , so that A 1 + A 2 = 2 8 1 3 3
Finally, we should scale up things by a factor d A 2 . Doing so, the areas scale up by a factor d A 2 4 = 3 2 8 . Furthermore, in order to count three pieces of each triangle area, multiply by 3. Thus we get: A = 3 2 8 × 3 × ( A 1 + A 2 ) = 1 3 3 and
A 2 = ( 1 3 3 ) 2 = 5 0 7
thanks for the solution.
(Drawing a diagram makes it clear that we should take the positive root.)
Allow me to point out that both roots are positive (for x). I guess u meant that y should take positive value.
Thanks. I really referred to using + rather than − at the place of ± , but the wording was a bit inaccurate, so I changed it and included my original free-hand sketching. P = ( x , y ) should be on she shortest segment of the unit circle connecting A and B . The diagram, showing the line (with positive slope) cutting the circle in two points, makes it clear that the wanted solution has the largest values for both x and y.
r=3.05505046330389 area squared=507. I first solved for the circle's radius (r) and then computed the altitudes to the two triangle types. That gave me the area of the figure, which squared to 507.
Let a and b be the central angles of the large triangle and small triangle respectively. Applying the Law of sines in each triangle, sin[(180 - a)/2]/r = [sin(a)]/4 and sin[(180 - b)/2]/r = [sin(b)]/2. Let b = 120 - a, equate each equation to r, and we get a non-linear equation for a, solved by Newton-Raphson. Approximate root is a =81.776 and b = 38.224. We then get r = 3.0545. Large triangle area = .5 r^2 sin(a) = 4.617. Small triangle area = .5 r^2 sin(b) = 2.886. Total area = 3*(large + small) = 22.51 and squared = 507.
hint: