Area problem
A B C D is a square with points E and F lying on sides C D and A D , respectively. If the purple area is [ B H G I ] = 1 2 0 , what is the sum of the pink areas [ A H F ] + [ F G E D ] + [ I C E ] ?
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
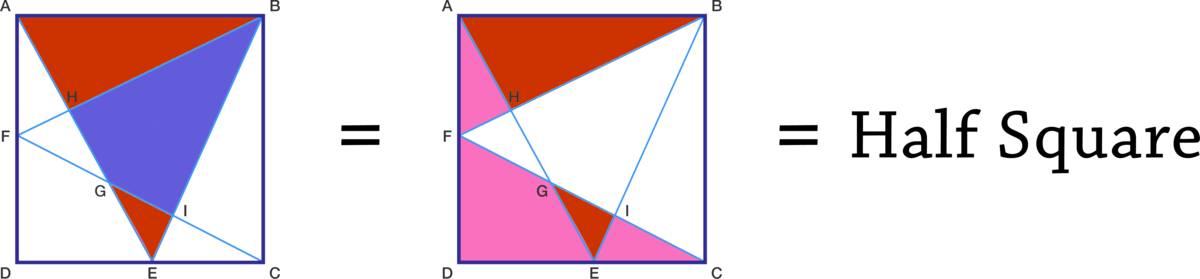 In each case, the area shaded is half of the area of the square. Since the red regions added are the same each time, the purple and pink areas must both have the same area of
1
2
0
.
In each case, the area shaded is half of the area of the square. Since the red regions added are the same each time, the purple and pink areas must both have the same area of
1
2
0
.
Simple and effective. Like all the best mathematics.
ok its half square....but from where does this half square came....i mean how do we know that its half square
Log in to reply
It's half the area of the square because it consists of a triangle with base = height = square side length:)
Log in to reply
Oh, man. DUH..
Log in to reply
@Alex Maione – shame....man...stop solving maths on ur imagination
Log in to reply
@A Former Brilliant Member – The sides of a square are equal....so the base and height becomes equal...basics
its not given that base,height and square side length are equal......:)
E and F are lying on the sides they arent the midpoints then how can you state that the area is half
Log in to reply
Because regardless of whether it's the midpoint, the area of the triangle is 0.5 b h. The base and height are each equal to the sides of the square. Therefore the triangle's area is 0.5*s^2. And the area of the square is simply s^2.
Lol am sorry i just realised my mistake
Not sure this is mentioned anywhere, so I'll say it: The name of this type of problem is a Carpet Theorem problem, and there are many other cool ones like it.
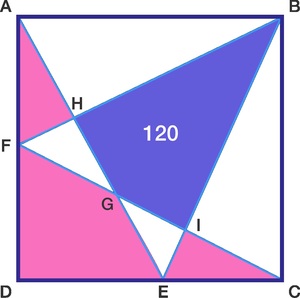
Let the area of the square [ A B C D ] = A s q u a r e , the blue area be A p u r p l e and the sum of the pink areas be A p i n k . Note that:
{ A p u r p l e + [ F G H ] + [ B C I ] A p i n k + [ F G H ] + [ B C I ] = [ B C F ] = [ A D E ] + [ B C E ] = 2 1 A s q u a r e = 2 1 A s q u a r e ⟹ A p i n k = A p u r p l e = 1 2 0
The title of the problem should be -"The Answer Lies Within"
Your explanation is valid only if the triangles are equal. If not, despite the answer be the same, your explanation doesn't apply.
Log in to reply
I think you mean if [ B C F ] = [ A D E ] + [ B C E ] . They are equal. As we have [ A D E ] = 2 1 × D C × B C and [ A D E ] + [ B C E ] = 2 1 × B C × D E + 2 1 × B C × E C = 2 1 × B C ( D E + E C ) = 2 1 × B C × D C = [ A D E ] .
It is correct for any partition.
Good work!
Clear explanation
This is a slight "cheating" answer, but since it is implied that a unique answer exists, the positions of points F on AD and E on DC shouldn't matter.
Slide point F to A and slide point E to C. Quadrilateral BHGI is now a right triangle, and half of the square. The pink areas form the other half of the square. So, under the assumption that there is a unique answer, the areas are the same.
My first thoughts also. Often times taking a problem to its limit shows a simple solution.
That's exactly what I did! Nice.
Incorrect If f and e moved to point d the area would be 0, it happens to work in this scenario but its not a proof.
Log in to reply
If F and E are moved to D, then the purple area will become zero. We know that it is 120, so this case will not work.
I'm sorry? For any math question, if I can determine that a variable's change does not affect the problem, and that changing this variable simplifies the problem greatly, I have every right to use this fact to my advantage.
The beginning of my answers says "This is a slight 'cheating answer' ", because it's obviously not a full proof. It's a shortcut to the answer.
Not incorrect. The problem did not ask for proof. It asked for a numerical answer. One can logically see that the statement of the problem implies that the simple case, where F is A and E is C, must hold.
moving F and E to D makes the square expand to infinity, so it is not a problem
Starting from Δ A F H and going in a clockwise rotation, designate the areas of the distinct regions as a , b , c , d , e , f , g , h . (In this designation, then, the areas of the red regions will be a , e , g , the area of the blue region will be c and the areas of the white regions b , d , f , h .)
Now as ∣ A F ∣ + ∣ F D ∣ is equal to the side length of the square, we know that ∣ Δ A B F ∣ + ∣ Δ F C D ∣ will equal half the area of the square. But so too will ∣ Δ A B E ∣ . Therefore
∣ Δ A B F ∣ + ∣ Δ F C D ∣ = ∣ Δ A B E ∣ ⟹ a + b + e + f + g = b + c + f ⟹ a + e + g = c .
But this just means that the sum of the areas of the 3 red regions is equal to that of the blue region, and so the desired sum is 1 2 0 .
How u say that ar(ABF)+ar(FCD) will half of the ar. Of square
Log in to reply
The area of Δ A B F is equal to 2 1 × ∣ A F ∣ × ∣ A B ∣ .
The area of Δ F C D is equal to 2 1 × ∣ F D ∣ × ∣ D C ∣ .
Since ∣ D C ∣ = ∣ A B ∣ , the sum of the areas of the two triangles is
2 1 ( ∣ A F ∣ + ∣ F D ∣ ) × ∣ A B ∣ .
But ∣ A F ∣ + ∣ F D ∣ = ∣ A D ∣ , so the sum of the areas is
2 1 × ∣ A D ∣ × ∣ A B ∣ , which is half the area of the square.
Area of the non-pink region equals |AEB|+|CFB| - 120 which equals |ABCD| - 120 (since |AEB| + |CFB| = |ABCD|).
Area of the pink region = |ABCD| - area of non-pink region = |ABCD| - (|ABCD| - 120) = 120
The answer is 120.
Let the areas of each part are as shown on the picture:
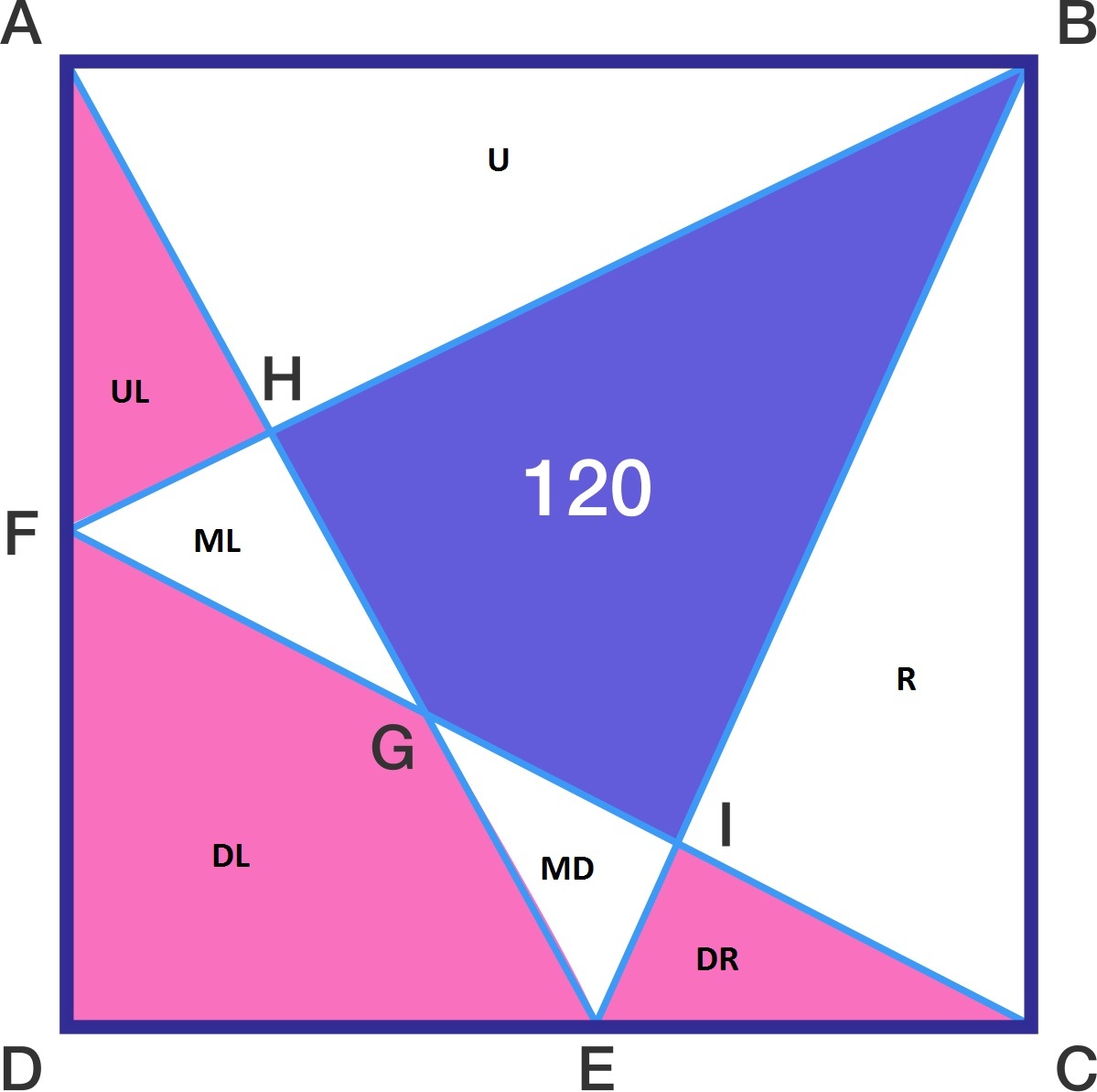 We can write and solve two equations for PA(PinkArea) = UL + DL + DR
We can write and solve two equations for PA(PinkArea) = UL + DL + DR
(1) [ABF]+[FCD]=[BCF] for any position of F on AD
(2) [DAE]+[EBC]=[ABE] for any position of E on DC
ML+120+R = UL+U+DL+MD+DR = PA+U+MD
U+120+MD = UL+ML+DL+R+DR = PA+R+ML
ML+120+R = PA+U+MD
+ U+120+MD = PA+R+ML
----------------------------------
ML+MD+U+R+240 = ML+MD+U+R+2PA -> 2PA=240 -> PA=120
I simply cheated with this one. Because I am lazy I simply made points F and G coincident with D and C the problem is then trivial. An engineers approach! ,
Reframing a problem.
[ A H B ] = [ F G E D ] + [ F H G ]
Half Square:
= [ A H B ] + [ F H G ] + 1 2 0
= [ A H B ] + [ F H G ] + [ A H F ] + [ I C E ] + [ F G E D ]
Then:
[ A H B ] + [ F H G ] + 1 2 0 = [ A H B ] + [ F H G ] + [ A H F ] + [ I C E ] + [ F G E D ]
1 2 0 = [ A H F ] + [ F G E D ] + [ I C E ]