Area Ratio
A B C is a triangle. Points D , E and F are on B C , C A and A B , respectively, such that D C B D = E A C E = F B A F = 2 . Let A D and B E intersect at P , B E and C F intersect at Q , and C F and A D intersect at R . What is the ratio [ A B C ] : [ P Q R ] ?
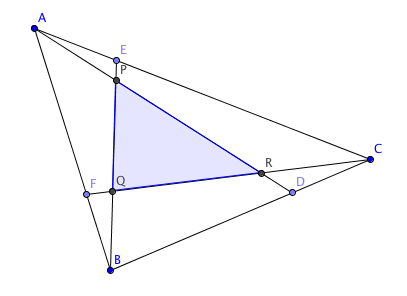
Details and assumptions
[ P Q R S ] represents the area of the figure P Q R S .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Moderator note:
Indeed! In fact, this particular version is also known as the one-seventh area triangle .
That's a great solution. Alternatively, after knowing that [ A B C ] [ A P E ] = [ A B C ] [ B Q F ] = [ A B C ] [ C R D ] = 1 / 2 1 , you could have said that the sum of those little triangles is the same as [ P Q R ] , from which the conclusion also follows.
Broke the tie. Great job!
Awesome buddy.I did the same initial steps and then finding area of few triangles and forming three equations and three variables.Then solving it easily gives us the answer....
We note that [ D C A ] = [ F B C ] = [ E A B ] = 3 [ A B C ] . Clearly, [ P Q R ] = [ A B C ] − [ D C A ] − [ F B C ] − [ E A B ] + [ Q F B ] + [ R D C ] + [ P E A ] = [ Q F B ] + [ R D C ] + [ P E A ] , since we need to subtract the areas of the three large triangle which are outside [ P Q R ] and then add back in their intersections, which we subtracted out twice.
Consider △ R D C : Its base has length 3 1 ⋅ B C . In order to find its area as a fraction of [ A B C ] , we must also find the ratio of its height to the height of △ A B C . By similar triangles, this is the same as finding D R : D A , which we can find using Menelaus's Theorem (ignoring the directed lengths) on △ A B D and segment C F : C D B C ⋅ R A D R ⋅ F B A F = 1 → 3 ⋅ R A D R ⋅ 2 = 1 → 6 ⋅ D R = R A → 7 ⋅ D R = D A , which means that the height of △ R D C is 7 1 times the height of △ A B C . Thus, [ R D C ] = 7 1 ⋅ 3 1 ⋅ [ A B C ] = 2 1 [ A B C ] .
Because of the symmetry in the problem, we use similar methods to find that [ Q F B ] = [ P E A ] = 2 1 [ A B C ] , and so we have [ A B C ] : [ P Q R ] = [ A B C ] : ( [ Q F B ] + [ P E A ] + [ R D C ] ) = [ A B C ] : 7 [ A B C ] = 7 .
How do you know that [DCA]=[FBC]=[EAB]=[ABC]/3?
Mass points:
Consider triangle △ A B C with cevians A D and C F that intersect at P such that D C B D = E A C E = 2 Now, let the mass at B be 1, and so the mass at C is 2, and the mass at A is 4 (since the cevians split the sides in a ratio 1:2). The mass at E is 6. Therefore, P E B P = 6 Now, we can solve. By the given ratios, [ A B E ] = [ A C D ] = [ B C F ] = 3 [ A B C ] The areas add to [ A B C ] , and don't include [ P Q R ] but include [ A E P ] , [ B F Q ] , and [ C D R ] twice. Therefore, [ P Q R ] = [ A E P ] + [ B F Q ] + [ C D R ] Now, by our ratio P D A P = 6 , [ A E P ] = 7 [ A E B ] [ B F Q ] = 7 [ B F C ] [ C D R ] = 7 [ C D A ] But we know [ A B E ] + [ A C D ] + [ B C F ] = [ A B C ] Therefore, [ P Q R ] = 7 [ A B C ] , and the answer is 7 .
Moderator note:
Good approach via mass points. It helps to simplify a lot of working (assuming you understand the theory).
Are there any books/papers that explains mass points (except for the berkeley math circle one)?
Log in to reply
Mass points does not really have much about it online; I mainly learned it through an online class (AoPS). The Berkeley math circle one seems okay (just to make sure we have the same link: http://mathcircle.berkeley.edu/archivedocs/2007_2008/lectures/0708lecturespdf/MassPointsBMC07.pdf)
Log in to reply
Yeah, I'm just wondering where you learned it from. Do you have any suggestions?
Log in to reply
@Harrison Lian – I learned it from an Art of Problem Solving course (look it up); I'm not sure which
Problems like this concerning area ratios may be easily attempted using Menelaus' Theorem or Ceva's Theorem. Since we cannot see cevian's here, so we will try using the other one.
Let's say [ A B C ] = 3 A . So using the information given in the problem, we have [ A B D ] = [ B E C ] = [ A F C ] = 2 A and similarly [ A D C ] = [ A B E ] = [ B F C ] = A .
Taking △ A B D and transversal as C F we obtain ∣ C D B C . R A D R . F B A F ∣ = 1 ⟹ R A D R = 6 1 ⟹ D A D R = 7 1
Likewise using the Theorem on △ ′ s A D C , B F C and taking the corresponding transversals we find A D A P = 7 3 , F C F Q = 7 1 ⟹ A D P R = 7 3 , F C Q R = 7 3 .
Now [ P Q R ] = [ P B R ] − [ Q B R ] = 7 3 . ( [ A B D ] − [ B F C ] ) = 7 A .
So the required ratio i.e. [ A B C ] : [ P Q R ] = A : 7 A = 7 which is our answer.
Let's call the triangles ABE,BCF,CAD "large" and the triangles AEP,BFQ,CDR "small". The area [PQR] can clearly be computed as follows: [ABC] minus (the areas of the three large triangles) plus (the area of the three small triangles).Clearly, we have [ABE]=[BCF]=[CAD]=[ABC]/3 and thus [PQR]equals the sum of the areas of the three small triangles.The task is affine: the ratios of the areas do not change as we deform the triangle. Thus we may just pick one specific triangle ABC and solve the task. One good choice is a right isosceles triangle with the right angle at B. For this triangle we can easily compute that [CDR]=[ABC]/21, which is by symmetry and affinity always true for all three small triangles for all choices of ABC. Thus [PQR]=3([ABC]/21)=[ABC]/7.
Quick question, how did 2 different people submit the exact same answer, letter for letter?
Log in to reply
Actually, I think 3 people copied Michal's solution word for word. I'm Not sure how, but some of the same people have done it on other problems, too.
They worked together, in the classroom !
Barycentric coordinates! http://www.artofproblemsolving.com/Resources/Papers/Bary_full.pdf
Thanks for share :)
We note that the ratios of areas, as well as ratios of collinear lengths, are preserved under linear transformation. Thus we are free to transform to the equilateral case.
For ease of calculation, let A B = B C = C A = 3 . By the law of cosines, we have ( B E ) 2 = ( A E ) 2 + ( A B ) 2 − 2 ⋅ A E ⋅ A B ⋅ cos ( 6 0 ∘ ) = 1 + 9 − 3 = 7 . Further, because this triangle is equilateral, it is easy to see through equality of angles that triangle P E A is similar to triangle A E B . Since E B = 7 E A , we square for the area ratio, giving [ P E A ] = 7 1 [ A E B ] . Also, since triangle A E B has the same height as the original triangle, but one third the base, [ A B C ] = 3 [ A E B ] .
Finally, as the equilateral triangle has symmetry, we set the areas equal:
[ A B C ] = 3 [ A E B ] − 3 [ A E P ] + [ P Q R ] = [ A B C ] − 7 1 [ A B C ] + [ P Q R ]
Thus we must have [ A B C ] = 7 [ P Q R ] , our answer.
First observe that [ABC] / 3 = [ABE] = [BCF] = [CAD]. Proof: [XYZ] equals half times basis time height. When properly chosen, the height of ABE equals the height of ABC with a smaller base (1/3). Similar for BCF and CAD.
Then observe that [PQR] = [APE]+[BQF]+[CRD]. Proof: [ABC] = [ABE] + [BCF] + [CAD] = [ABC] - [PQR] + [APE]+[BQF]+[CRD]. The first equation by the first observation, the second equation by checking the 7 smaller triangles that ABC is made of and observing that PQR wasn't counted and APE, BQF and CRD were counted twice.
Now construct an envelope UVW for ABC such that A, B and C lie on the sides UVW and such that the sides are parallel to the sides of PQR.
More specifically:
Draw 3 lines parallel to AD dividing DC in three equal parts (1/3, 2/3, through C). Draw 3 lines parallel to BE dividing AE in three equal parts (1/3, 2/3, through A). Draw 3 lines parallel to CF dividing BF in three equal parts. (1/3, 2/3, through B).
Observe the largest triangle that is now produced by the new lines through A, B and C forms an envelope for ABC..Mark the intersection of the new lines through B and C by U, the intersection of the new lines through A and C by V and the intersection of the new lines through A and B by W. Now the area between ABC and the envelope UVW consists of three triangles. The triangle ABW is as large as nine copies of triangle APE: three (mirrored) copies of triangle APE plus 3 paired copies of APE in parallelograms. So [ABW] = 9 x [APE]. Similarly, [BCU] = 9 x [BQF] and [ACV] = 9 x [CRD]. We can observe the total area of UVW in two ways:
1) Respecting ABC we see that [UVW] = [ABC] + 9 x ( [APE]+[BQF]+[CRD] ) = [ABC] + 9 x [PQR].
2) Looking at PQR only, and possible drawing extra lines parallel to the sides of PQR, we see that [UVW] = 16 x [PQR]. The triangle PQR has sides that are exactly 1/4 of the corresponding sides of UVW.
Combining 1 and 2 gives us [ABC] : [PQR] = 7.
This problem is a direct application of Routh's Theorem and it is specifically the case of the one-seventh area triangle so the answer is 7.
This a proof that uses vector algebra.
We will use the notation [ABC] to denote the area of the triangle, as indicated in the question.
We first note that [ A B E ] = [ B C F ] = [ C A D ] = [ A B C ] / 3 . ( # 1 ) This follows from A E / A C = B F / A B = C D / B C = 1 / 3 . ( # 2 ) The latter follows from, for example, A F / F B = 2 ⇒ A B / F B = 3 .
Area of the triangle ABC in terms of these traingles can be expressed as [ A B C ] = [ P Q R ] + [ A B E ] + [ B C E ] + [ C A D ] − ( [ A P E ] + [ B Q F ] + [ C R D ] ) Using (#1), the above equation reduces to [ P Q R ] = [ A P E ] + [ B Q F ] + [ C R D ] . ( # 3 )
One can use simple vector algebra to prove that A D / R D = B E / P E = C F / Q F = 7 . To do this, define B C = c and B A = a , find vectors B E and C F . Assume F Q / C F = x and B Q / B E = y . By equating vector B Q obtained from two different additions, B Q = B F + x F C = y B E , we can show that x = 1 / 7 and y = 3 / 7 . Thus, F Q / C F = 1 / 7 . The same result holds for other such ratios as well: P E / B E = R D / A D = 1 / 7 .
x = 1 / 7 implies that [ B F Q ] = [ C R D ] = [ A D C ] = [ A D C ] / 7 = [ A B C ] / 2 1 . By (#3), we must have [ P Q R ] = [ A B C ] / 7 .
Note on solving simultaneous equations involving vectors: If we have an equation of the form x a + y b = c , then, x , y can be solved by taking cross product of the quantities on the both sides with b and a respectively. This gives, x = ∣ a × c ∣ / ∣ a × b ∣ , y = ∣ c × b ∣ / ∣ a × b ∣ .
One method of solving this is through using areal coordinates . In this system, each point in the triangle is given coordinates of the form ( x , y , z ) with x + y + z = 1 , with A = ( 1 , 0 , 0 ) , B = ( 0 , 1 , 0 ) , C = ( 0 , 0 , 1 ) .
As described in the above link, the fact that D C B D = 2 implies that the line A D has equation 2 y = z . This could also be seen by finding D = ( 0 , 3 1 , 3 2 ) , since it's a third of the way between C and B . Similarly, the line C F has equation 2 x = y . R is at the intersection, with the following three equations -
2 y = z 2 x = y x + y + z = 1
These equations give x = 7 1 , y = 7 2 , z = 7 4 , which gives the coordinates of R . By cyclic interchange, we can immediately get that Q = ( 7 2 , 7 4 , 7 1 ) , P = ( 7 4 , 7 1 , 7 2 ) .
There is then a theorem, also in the link above, that given the three points P , Q , R in the triangle A , B , C , the area ratio [ A B C ] [ P Q R ] is given by -
[ A B C ] [ P Q R ] = ∣ ∣ ∣ ∣ ∣ ∣ p x q x r x p y q y r y p z q z r z ∣ ∣ ∣ ∣ ∣ ∣
using the determinant of a 3 × 3 matrix (this is provided that A = ( 1 , 0 , 0 ) , B = ( 0 , 1 , 0 ) , C = ( 0 , 0 , 1 ) or similar). With our P , Q , R , this gives
[ A B C ] [ P Q R ] = ∣ ∣ ∣ ∣ ∣ ∣ ∣ 7 4 7 2 7 1 7 1 7 4 7 2 7 2 7 1 7 4 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = 7 4 ∣ ∣ ∣ ∣ ∣ 7 4 7 2 7 1 7 4 ∣ ∣ ∣ ∣ ∣ − 7 2 ∣ ∣ ∣ ∣ ∣ 7 1 7 2 7 2 7 4 ∣ ∣ ∣ ∣ ∣ + 7 1 ∣ ∣ ∣ ∣ ∣ 7 1 7 4 7 2 7 1 ∣ ∣ ∣ ∣ ∣ = 7 1
Therefore, [ P Q R ] [ A B C ] = 7
Let's call the triangles A B E , B C F , C A D "large" and the triangles A E P , B F Q , C D R "small". The area [ P Q R ] can clearly be computed as follows: [ A B C ] minus (the areas of the three large triangles) plus (the area of the three small triangles).
Clearly, we have [ A B E ] = [ B C F ] = [ C A D ] = [ A B C ] / 3 and thus [ P Q R ] equals the sum of the areas of the three small triangles.
The task is affine: the ratios of the areas do not change as we deform the triangle. Thus we may just pick one specific triangle A B C and solve the task. One good choice is a right isosceles triangle with the right angle at B . For this triangle we can easily compute that [ C D R ] = [ A B C ] / 2 1 , which is by symmetry and affinity always true for all three small triangles for all choices of A B C . Thus [ P Q R ] = 3 ( [ A B C ] / 2 1 ) = [ A B C ] / 7 .
I think your solution is being copied by three other users.
 By applying Menelaus' theorem,we can easily get that,
P
D
P
A
=
Q
E
B
Q
=
R
F
C
R
=
4
3
⟹
[
B
P
D
]
[
B
A
P
]
=
[
C
Q
E
]
[
C
Q
B
]
=
[
A
F
R
]
[
A
R
C
]
=
4
3
.Now,we consider the
[
A
F
C
]
=
3
2
△
,and,
[
A
F
R
]
=
3
2
[
A
F
C
]
;
[
A
R
C
]
=
3
1
[
A
F
C
]
,this gives us that,
[
A
R
C
]
=
7
2
△
,we also have that,
△
=
[
P
Q
R
]
+
[
A
P
B
]
+
[
C
Q
B
]
+
[
A
R
C
]
=
[
P
Q
R
]
+
7
6
△
⟹
[
P
Q
R
]
=
7
1
△
.
By applying Menelaus' theorem,we can easily get that,
P
D
P
A
=
Q
E
B
Q
=
R
F
C
R
=
4
3
⟹
[
B
P
D
]
[
B
A
P
]
=
[
C
Q
E
]
[
C
Q
B
]
=
[
A
F
R
]
[
A
R
C
]
=
4
3
.Now,we consider the
[
A
F
C
]
=
3
2
△
,and,
[
A
F
R
]
=
3
2
[
A
F
C
]
;
[
A
R
C
]
=
3
1
[
A
F
C
]
,this gives us that,
[
A
R
C
]
=
7
2
△
,we also have that,
△
=
[
P
Q
R
]
+
[
A
P
B
]
+
[
C
Q
B
]
+
[
A
R
C
]
=
[
P
Q
R
]
+
7
6
△
⟹
[
P
Q
R
]
=
7
1
△
.
How do you know that [BQF] = [APE] = [X]
I will present a very elementary solution (Puzzle Idea).Please, draw your own figure. Let the line segments AQ, BR and CP. We obtain ten distinct zones / pieces. I will use 11 letters for areas: [APE]=a, [CPE]=b, [CPR]=c, [CRD]=d, [BRD]=e, [BRQ]=f, [BQF]=g, [AQF]=h, [APQ]=i, [PQR]=j and [ABC]=s. The main assumption is that ratio [ABD] : [ACD]= 2, because ratio BD:CD =2 (and the straights / altitudes of triangles are the same). Firstly, in triangle ADC, a+b+c+d=s/3. Analogical, d+e+f+g =s/3 and g+h+i+a = s/3. Adding these relations, we obtain a+d+g+s-j=s, a+d+g=j . In triangle APC, b=2a. Analogical, e=2d and h=2g. Here, we have b+e+h = 2(a+d+g) = 2j . After that, in triangle AQC, c+j = 2i, in triangle PBC, f+j=2c and in triangle RAB, i+j=2f. So, adding these, c+i+f=3*j . In conclusion s=(a+d+g)+(b+e+h)+(c+f+i)+j, s=j+2j+3j+j, s=7j, so the ratio [ABC]:[PQR]=7 . I hope that you will enjoy this solution :)
Draw your own figure. You will like the map, for sure :)
Let's call the
Δ
ABE,
Δ
BCF,
Δ
CAD "large" and the
Δ
AEP,
Δ
BFQ,
Δ
CDR "small".
The area [PQR] can clearly be computed as follows: [ABC] minus (the areas of the three large triangles) + (the area of the three small triangles).
Clearly, we have [ABE]=[BCF]=[CAD]=
3
[
A
B
C
]
and thus [PQR] equals the sum of the areas of the three small triangles.
The task is: the ratios of the areas do not change as we deform the triangle.
Thus we may just pick one specific
Δ
ABC and solve the task.
One good choice is a right isosceles triangle with the right angle at
B
.
For this triangle we can easily compute that [CDR]=
2
1
[
A
B
C
]
, which is by symmetry and affinity always true for all three small triangles for all choices of
A
B
C
.
Thus [PQR]=
3
2
1
[
A
B
C
]
=
7
[
A
B
C
]
⇒[ABC]:[PQR] =
7
:
1
So, the answer is
7
Let's call the triangles ABE,BCF,CAD "large" and the triangles AEP,BFQ,CDR "small". The area [PQR] can clearly be computed as follows: [ABC] minus (the areas of the three large triangles) plus (the area of the three small triangles).Clearly, we have [ABE]=[BCF]=[CAD]=[ABC]/3 and thus [PQR]equals the sum of the areas of the three small triangles.The task is affine: the ratios of the areas do not change as we deform the triangle. Thus we may just pick one specific triangle ABC and solve the task. One good choice is a right isosceles triangle with the right angle at B. For this triangle we can easily compute that [CDR]=[ABC]/21, which is by symmetry and affinity always true for all three small triangles for all choices of ABC.
Thus [PQR]=3([ABC]/21)= [ABC]/7.
Let's call the triangles ABE,BCF,CAD "large" and the triangles AEP,BFQ,CDR "small". The area [PQR] can clearly be computed as follows: [ABC] minus (the areas of the three large triangles) plus (the area of the three small triangles).Clearly, we have [ABE]=[BCF]=[CAD]=[ABC]/3 and thus [PQR]equals the sum of the areas of the three small triangles.The task is affine: the ratios of the areas do not change as we deform the triangle. Thus we may just pick one specific triangle ABC and solve the task. One good choice is a right isosceles triangle with the right angle at B. For this triangle we can easily compute that [CDR]=[ABC]/21, which is by symmetry and affinity always true for all three small triangles for all choices of ABC. Thus [PQR]=3([ABC]/21)=[ABC]/7.
By using Menelaus' Theorem for triangle A C D with B , P , E are collinear, we have : E C E A ⋅ B D B C ⋅ P A P D = 1 . Therefore, P D P A = E C E A ⋅ B D B C = 2 1 ⋅ 2 3 = 4 3 Then A D A P = 7 3 . Hence, [ A B C ] [ A P E ] = [ A D C ] [ A P E ] ⋅ [ A B C ] [ A D C ] = A D A P ⋅ A C A E ⋅ B C C D = 7 3 ⋅ 3 1 ⋅ 3 1 = 2 1 1 . Then we have [ A B C ] [ A B P ] = [ A B C ] [ A B E ] − [ A P E ] = 3 1 − 2 1 1 = 7 2 . By using similar arguments, we obtain [ A B C ] [ C Q B ] = [ A B C ] [ A R C ] = 7 2 . Therefore [ A B C ] [ P Q R ] = [ A B C ] [ A B C ] − [ A B P ] − [ B C Q ] − [ C A R ] = 1 − 3 ⋅ 7 2 = 7 1 , or equivalently, [ P Q R ] [ A B C ] = 7 .
Remark . By using similar arguments, we can prove a general theorem : Routh's Theorem .