Area to Length?
Two faces of a rectangular cuboid have areas 2 0 and 1 8 . Find the minimum possible length of its space diagonal, to three decimal places.
The answer is 7.3358.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Like the use of AM-GM instead of calculus
How is the space diagonal (a sq.+b sq.+c sq.)^2. Am I missing a point? Please explain that concept. Is there a wiki I can refer?
Log in to reply
Maybe you mean (a sq. + b sq. + c sq.)^(1/2). It follows from Pythagorean theorem. Let x - diagonal of the base and h - hight of rectangular parallelepiped. Diagonal of the base is x=(a^2+b^2)^(1/2). Therefore space diagonal is equale (x^2+h^2)^(1/2) = (a^2 + b^2 + c^2)^(1/2). I hope it will help you)
This way... I'm really shoked!
What is AM-GM? Is there a wiki for it?
Log in to reply
Posting URLs with underscores doesn't seem to work properly, so I ran it through google's URL shortener...
Inequality of arithmetic and geometric means
goo.gl/gM9na3
We have the two conditions a b = 2 0 and b c = 1 8 . Multiply the second equation by a to get a b c = 1 8 a ⟹ 2 0 c = 1 8 a ⟹ c = 1 0 9 a . We also have, from the first equation, that a = b 2 0 .
With this information, we want to minimize d = a 2 + b 2 + c 2 which is actually equivalent to minimizing d 2 = a 2 + b 2 + c 2 and this is much easier to differentiate. Plugging in the previous equations we have that d 2 = b 2 b 4 + 7 2 4 and the derivative with respect to b of this is 2 b − 1 4 4 8 b − 3 and setting this equal to 0 we get b = 2 4 1 8 1 .
Plugging this into our expression for d we find that d 2 ≈ 5 3 . 8 1 4 5 and thus d ≈ 7 . 3 3 5 8 4 .
Exactly my solution :D
You can simplify your differentiation. Create a new variable t = b^2. Differentiate with respect to t instead of b.
Should be 2b-1448 b^-3 in your solution, not 2b-1488 b^-3.
Perhaps I’m missing something in above. If I have 2b - (2)(724)(b^-3) = 0, I essentially have 2b^4 - 1448 = 0 which is 2b^4 = 1448 and then b^4 = 724. The 4th root of b is 5.16 approximately. Since everybody is getting the same answer what did I miss?
Log in to reply
724 = 4 times 181 so when you take the fourth root you get 2^(1/2) 181^(1/4) which is approximately 5.18. But then you need to plug that in the formula for the distance.
We minimize the function f ( a , b , c ) = a 2 + b 2 + c 2 under the conditions a b = 2 0 , a c = 1 8 .
The total derivatives of these expressions are ⎩ ⎪ ⎨ ⎪ ⎧ 2 a d a + 2 b d b + 2 c d c = 0 a d b + b d a = 0 a d c + c d a = 0 Multiply the first equation by a / 2 , the second by − b , the third by − c ; then add: a 2 d a − b 2 d a − c 2 d a ( a 2 − b 2 − c 2 ) d a + a b d b − a b d b + a c d c − a c d c = 0 = 0 = 0 = 0 . Thus the solution is characterized by the fact that a 2 = b 2 + c 2 . Multiply by a 2 : a 4 − ( a b ) 2 − ( a c ) 2 = 0 . Substitute the known values for a b and b c to obtain a 2 = 2 0 2 + 1 8 2 . The fact that b 2 + c 2 = a 2 provides a shortcut to find the body diagonal D : D 2 = a 2 + ( b 2 + c 2 ) = 2 a 2 = 2 2 0 2 + 1 8 2 = 4 1 8 1 , D = a 2 + b 2 + c 2 = 2 4 1 8 1 ≈ 7 . 3 3 6 .
Why can't we do it in this way.... Upper rectangle 10 × 2.. and it's diognal will be sqrt(100 + 4 ) which can be used as the base of a new triangle consisting of the perpendicular 9, diagonal of upper rectangle as base and the diagnol of the body as hypotenus.. . H ^2 = B^2 + P ^2 = 104 + 81 H = sqrt ( 185 ) = 13.601
Please correct me if I'm wrong
Log in to reply
You are assuming that the rectangle has dimensions 10 x 2. Why not 5 x 4, or 15 x 4/3, or ...? (Note that it is not said that the sides are integers.)
That does not satisfy the requirement to finding the minimum possible value of the diagonal.
Does it necessarily follow that a minimum for D^2 is also a minimum for D?
Log in to reply
Yes. If a function f is monotonously increasing, then the minimum of x produces a minimum of f ( x ) .
Nicely done! You've avoided using AM-GM altogether. Which is better than mine! +1
Relevant wiki: Lagrange Multipliers
Since I literally just read the short section on Lagrange Multipliers in my calculus textbook, I thought I'd try applying it to this question. (The passage is much more basic than the related wiki on this site, so my notation might be a bit on the simplistic side.)
We are effectively trying to minimize d 2 = f ( x , y , z ) = x 2 + y 2 + z 2 , subject to constraints g ( x , y , z ) = x y = 1 8 and h ( x , y , z ) = x z = 2 0 .
The Lagrange condition is ∇ f = λ ∇ g + μ ∇ h which written in terms of its components would be f x f y f z = λ g x + μ h x = λ g y + μ h y = λ g z + μ h z [Note: f x , f y and f z are the partial derivatives w.r.t. x , y and z respectively.]
Applying this to our functions, and combining with our constraints gives us the system \begin{aligned} 2x&=\lambda y+\mu z \tag{1}\\ 2y&=\lambda x \tag{2}\\ 2z&=\mu x \tag{3}\\ xy&=18 \tag{4}\\ xz&=20 \tag{5}\\ \end{aligned} Multiplying equation (1) by x , equation (2) by y and equation (3) by z yields 2 x 2 2 y 2 2 z 2 = λ x y + μ x z = λ x y = μ x z which immediately leads to x 2 = y 2 + z 2 . From there we proceed as follows: x 4 x 4 x 2 = x 2 y 2 + x 2 z 2 = 1 8 2 + 2 0 2 = 2 1 8 1 ( multiplying by x 2 ) ( substituting our constraints ) This is all we need to calculate the length of the diagonal. d d d d = x 2 + y 2 + z 2 = 2 x 2 ( since x 2 = y 2 + z 2 ) = 2 4 1 8 1 ≈ 7 . 3 3 6 Strictly speaking, the Lagrange Multiplier method will identify maximum and/or minimum values, assuming these extreme values exist . So the above shows that if the space diagonal in question has a minimum length, it would be ≈ 7 . 3 3 6 .
Regarding your last line: I thought you have only shown that d ≈ 7 . 3 3 6 is a critical point. How do you mean it must be a minimum point? Maybe it could be a saddle point?
Log in to reply
You're right; I re-read the text and noticed it mentioned "if the values exist" which I missed the first time. I've updated the last line to reflect this; thanks for pointing it out!
Log in to reply
But should you assume that the minimum value exists?
Log in to reply
@Pi Han Goh – Well, how could it not? You could try substituting in for values of a , b , c which make d diverge, namely lim a → 0 , but those make d tend to positive infinity. This means a minimum exists, right?
To be sure 7 2 4 4 1 , 7 2 4 4 1 2 0 , 7 2 4 4 1 1 8 is indeed a minimum - well, a maximum certainly doesn't exist, and a minimum certainly does. Since this is the only extreme point, it follows that this is indeed the minimum.
Log in to reply
@Ivo Zerkov – Fair enough. Thanks man.
Is it possible to produce a maximum length?
Log in to reply
Nope - making the common side between the 20 and 18 walls, in this case x , exceedingly small yields an exceedingly long diagonal.
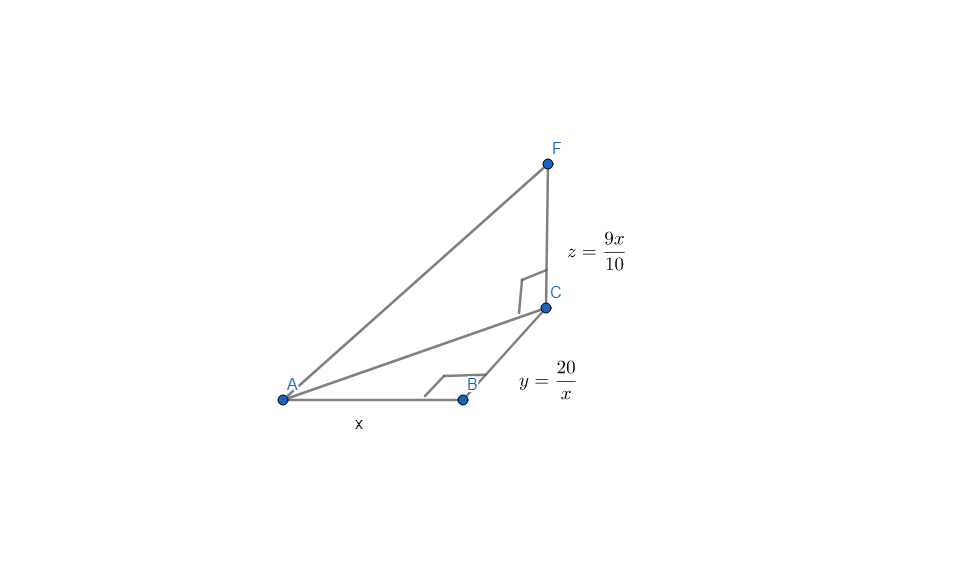
x y = 2 0 and z y = 1 8 ⟹ y = x 2 0 ⟹ z = 1 0 9 x
⟹ D ( x ) = d 2 ( x ) = 1 0 0 1 8 1 x 2 + x 2 4 0 0 ⟹ d x d D = 5 0 1 8 1 x − x 3 8 0 0 = 5 0 x 3 1 8 1 x 4 − 8 0 0 ∗ 5 0 = 0 ⟹
x 4 = 1 8 1 1 0 4 ∗ 4 ⟹ x = 1 8 1 1 / 4 1 0 2 for x > 0 .
Testing for relative min using second derivative: d x 2 d 2 D = 5 0 1 8 0 − x 4 2 4 0 0
x = 1 8 1 1 / 4 1 0 2 ⟹ d x 2 d 2 D = 2 5 − 1 8 1 < 0 ⟹ min at x = 1 8 1 1 / 4 1 0 2 .
∴ d 2 = 4 1 8 1 ⟹ d = 2 4 1 8 1 ≈ 7 . 3 3 5 8
Relevant wiki: Applying the Arithmetic Mean Geometric Mean Inequality
Let the dimensions of this cuboid be a , b , c such that a b = 2 0 , a c = 1 8 . We want to find the minimum value of d : = a 2 + b 2 + c 2 .
From a b = 2 0 , a c = 1 8 , we get b = a 2 0 , c = a 1 8 . Thus, a 2 + b 2 + c 2 = a 2 + ( a 2 0 ) 2 + ( a 1 8 ) 2 = a 2 + a 2 7 2 4 .
By arithmetic mean geometric mean inequality , A M ( a 2 , a 2 7 2 4 ) ≥ G M ( a 2 , a 2 7 2 4 ) ⇔ a 2 + a 2 7 2 4 ≥ 2 a 2 ⋅ a 2 7 2 4 = 2 7 2 4 .
Thus, the minimum value of d is 2 7 2 4 = 2 4 1 8 1 ≈ 7 . 3 3 6 and it occurs when a 2 = a 2 7 2 4 , or equivalently, when its dimensions are 4 7 2 4 , 4 7 2 4 2 0 , 4 7 2 4 1 8 .
The rectangular cuboid have sides a , b , c and the conditions are: a c = 2 0 and b c = 1 8 . The diagonal d is going to be d 2 = a 2 + b 2 + c 2 .
From this we have: a = c 2 0 b = c 1 8
We can plug this into the equation for the diagonal:
d 2 = ( c 2 0 ) 2 + ( c 1 8 ) 2 + c 2
Considering only the real and positive solution:
d = c 7 2 4 + c 4
With this formula for the diagonal we can find the minima by looking at the derivative and making it equal to zero.
( c 7 2 4 + c 4 ) ′ = 0
By using the chain rule and the division rule we get:
c 2 2 1 ( 7 2 4 + c 4 ) − 2 1 4 c 3 c − 1 7 2 4 + c 4 = 0
After some algebra we get that the minimum value for c is 4 7 2 4 .
Plugging the value into the original formula:
d = c 7 2 4 + c 4
d = 4 7 2 4 7 2 4 + 4 7 2 4 4
And we get the minimum value for d :
d = 2 4 1 8 1 ≈ 7 . 3 3 5 8
Let x be the length of the edge joining the 20 and 18 faces. Then the dimensions of the cuboid are x , x 2 0 and x 1 8 .
So the length of the diagonal is
d = x 2 + ( x 2 0 ) 2 + ( x 1 8 ) 2
This is minimised when d 2 = x 2 + ( x 2 0 ) 2 + ( x 1 8 ) 2 = x 2 + x 2 7 2 4 is minimised
With a little simple calculus, solve d x d d 2 = 2 x − 2 x 3 7 2 4 = 0 or x = 4 7 2 4 = 5 . 1 8 7
Substituting back into the first equation d = 7 2 4 + 7 2 4 7 2 4 = 2 7 2 4 = 4 1 8 1 = 2 4 1 8 1 = 7 . 3 3 5 8
let a = 20k then b = 1/k (ab = 20)
and then c = 18k (bc = 18)
space diagonal squared = d 2 = a 2 + b 2 + c 2 = 7 2 4 k 2 + k 2 1 ≥ 2 × 7 2 4 ; ( A . M ≥ G . M )
Therefore min. value of d = 2 7 2 4 = 7 . 3 3 5 8
Its acually much simpler then what many of you are saying. It is simply that the smallest perimeter for any are of a rectangle is a square. Therefore the sidelengths of the two squares are √20 and √18 . Using the Pythagorean theurum, you get √20² + √18² = C² . Cross out the sqrts and squares to get 20 + 18 = C². 38 = C² C = √38 Now using pythagorus again using the height now that you have the diagonal of the ground segment, you want to use that diagonal with the height. Which is √18² + √38² = C². 18 + 38 = C² --> C = √58 or 7.3358...
It will be √56 and √58 is = 7.61577311
Let "a" and "b" be the length of the rectangle which area is 20 Let "a" and "c" be the length of the rectangle which area is 18 ab = 20; ac = 18; b/c = 20/18;
Diagonal D would be: D^2 = a^2 + b^2 + c^2 D^2 = (18/c)^2 + (10c/9)^2 + c^2} ; manipulating to have just one variable Using Minima and Maxima theorem, set dD/dc to 0 you will get: c = 3.47
Substituting c to the Diagonal D equation....
D = 7.335836434
Let l , w , h be the length, width, and height of the rectangular cuboid. This allows us to write:
l w = 2 0
h w = 1 8
Now, we write d all in terms of our edges, l , w , and h :
d = l 2 + w 2 + h 2
We can further simplify this equation by recognizing that l and h can be written in terms of w , cutting our variable count from 3 to 1:
l = w 2 0
h = w 1 8
d = ( w 2 0 ) 2 + w 2 + ( w 1 8 ) 2
Then we expand the two fractions and add the like terms:
d = w 2 + w 2 7 2 4
Next, we can find the minimum value of the variable in a quadratic equation by finding when the the first derivative of that equation equals 0. To make this a bit easier to work with, we'll square both sides of the above equation, and then let f ( w ) = d 2 for conventions:
d 2 = w 2 + w 2 7 2 4 = f ( w )
Next, we evaluate the first derivative of f ( w ) , f ′ ( w ) (note: I rewrote w 2 7 2 4 as 7 2 4 w − 2 beforehand as a personal preference; I find it makes differentiating easier):
f ′ ( w ) = 2 w − 1 4 4 8 w − 3
Now that we have our first derivative, we need to solve for when f ′ ( w ) = 0 . This will happen when 2 w = 1 4 4 8 w − 3 . The rest is algebra:
2 w = 1 4 4 8 w − 3
2 w 4 = 1 4 4 8
w 4 = 7 2 4
w = ± 5 . 1 8 7 2 1 . . .
Since the side of a cuboid cannot be negative, the minimum value of our width, w , is approximately 5 . 1 8 7 2 1 . This can then be plugged back into our equation for d to get our final answer:
d = 5 . 1 8 7 2 1 2 + ( 5 . 1 8 7 2 1 ) 2 7 2 4 = 7 . 3 3 5 8
It is easy to note that, ac=20; bc=18;
Now, we need to find the diagonal length which is √a^2 + b^2 + c^2 (It can be obtained using pythagoras theorem). Applying AM - GM inequality in terms (a^2 + b^2) and c^2; - We come up with {a^2 + b^2 + c^2 }/2 ≧ √ [ {a^2 + b^2} * c^2 ] ; so, a^2 + b^2 + c^2 ≧ 2 * √ (ac)^2 + (bc)^2 ; Putting values and solving, Least value of a^2 + b^2 + c^2 is 53.814; But d = √a^2 + b^2 + c^2 ; = √53.814 ; = 7.3358 ;
The minimum length of d is 7.33583643 when b=5.1872.
bc=18, c=18/b
ab=20, a=20/b
d^2=a^2+b^2+c^2
d^2=400/b^2+b^2+324/b^2 . Instead of finding derivative
and then calculate the value,
I decided to write a small program.
First I ran b from 1 to 9 with step 1
Then - from 4 to 6 with step .1 and couple more times ... ,
This way I narrowed the range for b and visually found the value for b with minimal d.
for b = 5.185 to 5.189 step .0001
b2 = b^2
d2 = (400/b2)+b2+(324/b2)
d = sqr(d2)
print b,d
next b
How do you know that 1 ≤ b ≤ 9 must be fulfilled? Maybe 0 < b ≤ 1 or b > 9 could be true?
We need to minimize
d
=
a
2
+
b
2
+
c
2
, where
a
,
b
,
c
are the 3 sides of the cuboid. We see that the area condition can be reformulated so they're dependent on 1 variable.
a
⋅
b
=
1
8
→
b
=
a
1
8
and
a
⋅
c
=
2
0
→
c
=
a
2
0
. Now we have a function of 1 variable
f
(
a
)
=
a
2
+
(
a
1
8
)
2
+
(
a
2
0
)
2
.
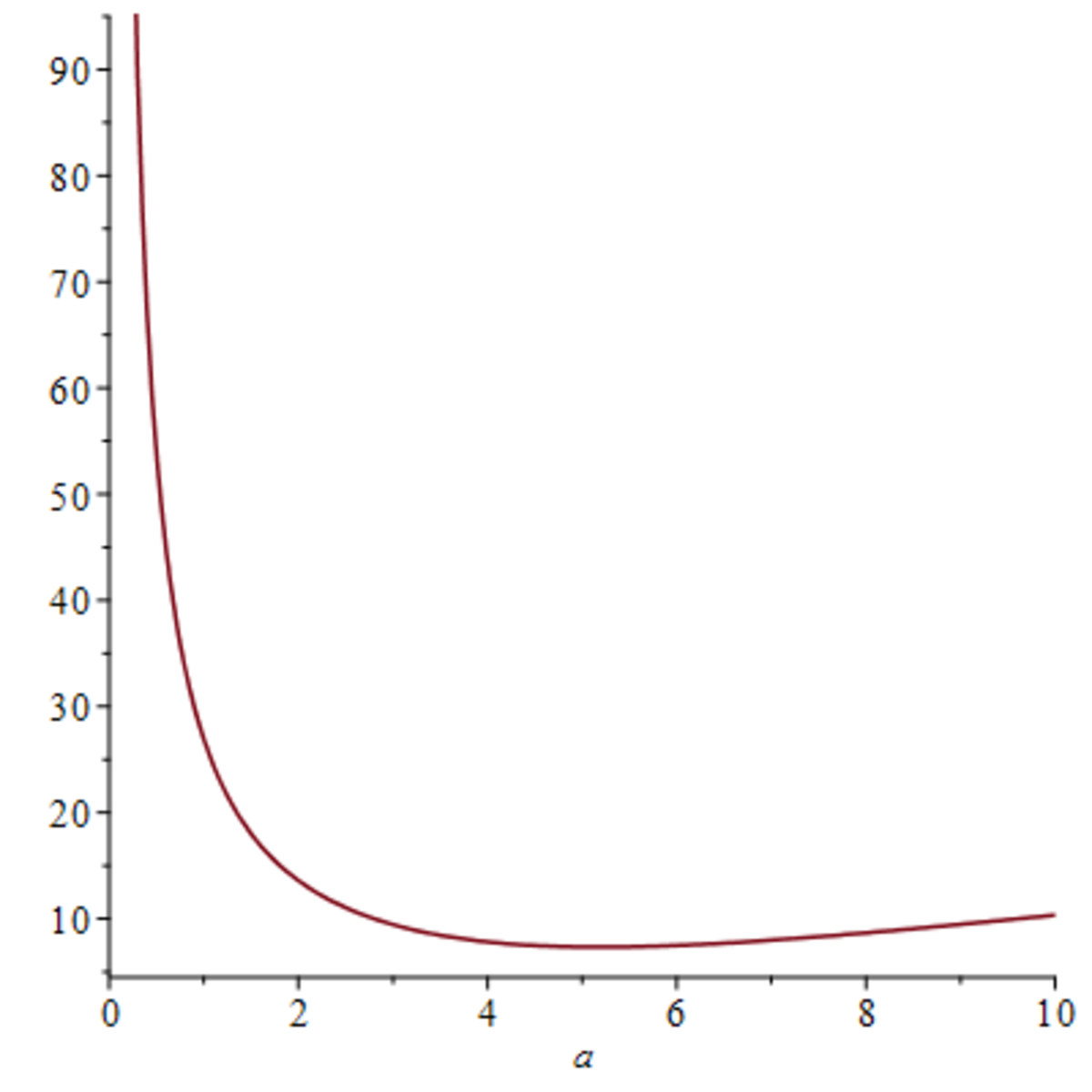
Now we solve the f ′ ( a ) = 0 , and we'll only look at solutions a ≥ 0 , and we get the solution a ≈ 7 . 3 3 5 8 3 6 4 3 4 .

Let a , b , c be the side lengths of the prism. Since the areas of the faces are different, they cannot be opposite one another. So WLOG, we can write
a b b c = 2 0 = 1 8 .
From the second equation, we have b = c 1 8 . Plugging this into the first equation yields 1 8 a = 2 0 c , or a = 9 1 0 c . This eliminates the variable a , and the two conditions become one condition: b c = 1 8 .
The length of the space diagonal of the prism is equal to
a 2 + b 2 + c 2 = ( 9 1 0 c ) 2 + b 2 + c 2 = b 2 + 8 1 1 8 1 c 2 .
By the AM-GM inequality,
b 2 + 8 1 1 8 1 c 2 ≥ 2 b 2 ( 8 1 1 8 1 c 2 ) = 2 b c ( 9 1 8 1 ) = 2 ( 1 8 ) ( 9 1 8 1 ) = 4 1 8 1 .
Therefore, the minimum possible length of the space diagonal is 4 1 8 1 ≈ 7 . 3 3 5 8 . Equality holds when b 2 = 8 1 1 8 1 c 2 , so that
( a , b , c ) = ( 4 1 8 1 1 0 2 , 2 ⋅ 4 1 8 1 , 4 1 8 1 9 2 ) ≈ ( 3 . 8 5 7 , 5 . 1 8 7 , 3 . 4 7 0 ) .
EDIT: I just realized there was a more direct way to apply AM-GM to solve the problem:
a 2 + b 2 + c 2 ≥ 2 b 2 ( a 2 + c 2 ) = 2 ( a b ) 2 + ( b c ) 2 = 2 2 0 2 + 1 8 2 = 4 1 8 1 .
Thus, the minimum possible length of the space diagonal is 4 1 8 1 = 2 4 1 8 1 . This method can also be generalized: if two faces of a rectangular cuboid have areas A and B , where A = B , then the minimum possible length of its space diagonal is 2 A 2 + B 2 .