Areas in rectangles
The area of the whole rectangle is 160 and the area in red is 12.
What is the area in green?
The answer is 92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Where is the proof that a + b + 12 = 40? Ed Gray
Log in to reply
The triangle made up by a + b + 1 2 + 4 0 = 2 1 6 0 = 8 0 is half the area of the rectangle. Subtract 40 from both sides a + b + 1 2 = 4 0 .
Log in to reply
Chew, thanks, but I took a short-cut, because I agree that the upper green is 40. I should have asked for a proof that a + b + 12 + 40 = Half the rectangle. Regards, Ed Gray. I know it looks that way, but that is not sufficient.
Log in to reply
@Edwin Gray – It is that way, but it is easier to explain mentioning the half area.
im a child and i know the answer
Log in to reply
Wise beyond your years - a prodigy! Now it's way past your bedtime...
Why is it 1/4? It's not a square...
Log in to reply
Let the height and base breadth of the rectangle by h and b respectively. Then the area of the rectangle is h b . Now the green triangle has the same base b but half the height. Its area is given by 2 1 × 2 h × b = 4 1 h b .
Actually the two diagonals of the rectangle divide the rectangle into four equal parts.
How to know that a+b+12+40=half rectangle?
Log in to reply
Notice the triangle made up by a + b + 1 2 + 4 0 has the base b and height h same as those of the rectangle. Its area A △ = 2 1 b h and the area of the rectangle is A rectangle = b h .
Half of that rectangle is Pythagoras triangle. When a straight line is drawn from the 90° angle to the mid point of the hypothenus. The two triangle formed are not equal in area, how then is ¼(area of rectangle)= area of triangle
Log in to reply
Let the base and height of rectangle be b and h . Then the area of rectangle is A = b h . The top triangle has the same base b but only a height of 2 h . Then the area of triangle A △ = 2 1 × b × 2 h = 4 b h = 4 1 A . That is 4 1 of the area of rectangle.
Label each region A through H , as follows:
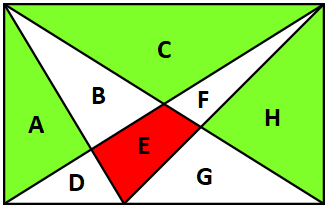
Then C is a triangle that is 4 1 the area of the whole rectangle, so C = 4 1 1 6 0 = 4 0 . Also, A + B is a triangle that is 4 1 the area of the whole rectangle, so A + B = 4 0 .
The triangle made from B , E , and G and the triangle made from G and H have the same base and height, so their areas are the same, which means B + E + G = G + H . We are given that E = 1 2 , so this simplifies to B = H − 1 2 .
Substituting B = H − 1 2 into A + B = 4 0 gives A + ( H − 1 2 ) = 4 0 , or A + H = 5 2 .
The green areas are A , C , and H , and A + C + H = ( A + H ) + C = 5 2 + 4 0 = 9 2 .
There is a -print in the solution. It should say that The green areas are A,C, and H, and A + C + H = (A + H) + C = 52 + 40 = 92. I got a different solution; maybe someone can find the error which should be obvious. Consider the triangle composed of C,B,E, and F. It has an area of (1/2)(bh) = (1/2)(160) = 80. So C + B + F + E = 80, and C + B + F = 68, Then B + F = 68 - C. Now consider the triangle composed of D, E, and G. It has an area of (1/2)(bh) = (1/2)(80) = 40. Since E = 12, D + G =40 - 12 = 28. The sum of the white areas is B + F + D + G = 68 - C + 28 = 96 - C. But the sum of the white areas plus the sum of the green areas + E = 160. (There's my mistake; I had absent-mindedly written 180, instead of 160). So B + F + D + g + A + C + H + E = 160, or B + F + D + E = 160 - 12 - (A + C + H) = 148 148 - (A + C + H). Then the green sum is A + C + H = 148 - (96 - C), or C + 52 , or A + H = 52. But C = 40, so the sum of greens = 92. Thanks for the help, Ed Gray
Log in to reply
I fixed my solution, thanks! I'm also glad you were able to find your mistake.
At first this problem seemed difficult. But then, old school geometry properties started to flash in my mind and the problem became a lot easier, just like you did.
Well said. :) Simple yet CLEAR. It's like a proof well stated. :)
Please prove c is 1/4 of the rectangle.
Log in to reply
Area of triangle c = 1/2 * Base of triangle c * Perpendicular height of triangle c
Base of triangle c = Base of rectangle. Perpendicular height of triangle c = 1/2 * Height of rectangle (because diagonals of a rectangle meet at the centre)
Therefore, area of triangle c = (1/2) * (Base of rectangle) * (1/2 * Height of rectangle) = 1/4 * Area of rectangle
Half of that rectangle is Pythagoras triangle. When a straight line is drawn from the 90° angle to the mid point of the hypothenus. The two triangle formed are not equal in area, how then is ¼(area of rectangle)= area of triangle
As you go, A+D=D+E+F Whole green→80+12=92
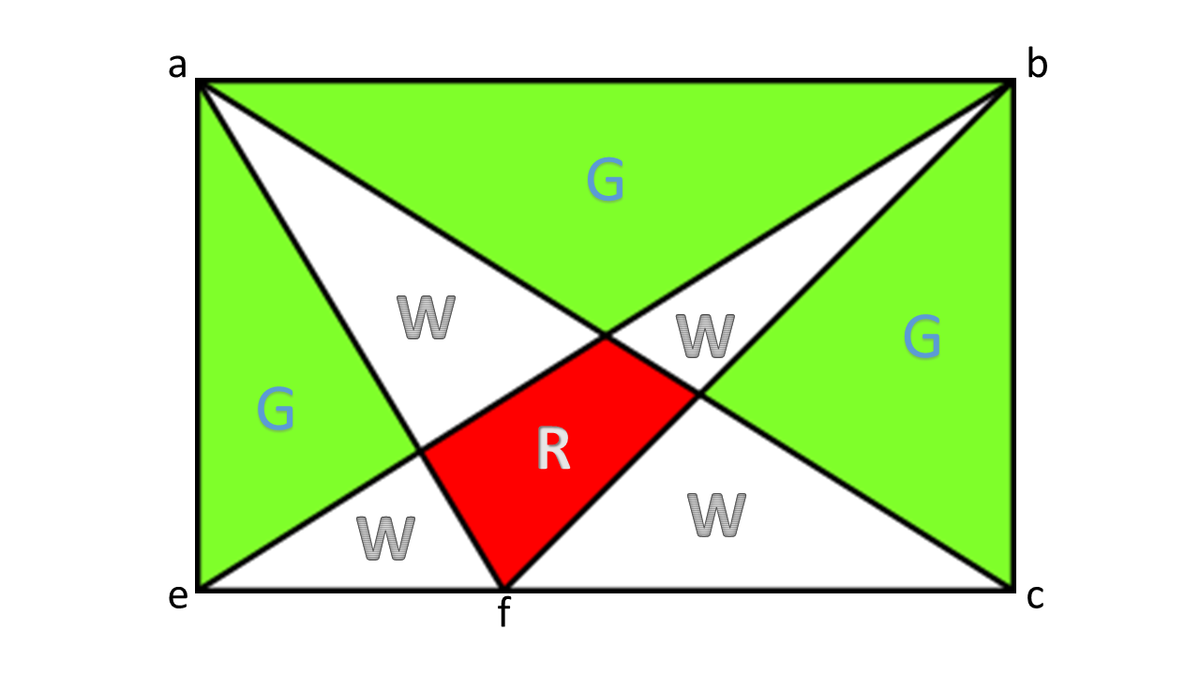
Looking at the picture above:
Green area G = Rectangle area - (White area W + Red area R ) ------- 1
Now to calculate the white area, we know that the sum area of the two triangles a f c and b f e equal to the half of the rectangle area:
Triangles area = 0 . 5 ∗ e f ∗ b c + 0 . 5 ∗ f c ∗ b c = 0 . 5 ∗ ( e f + f c ) ∗ b c = 0 . 5 rectangle area, and also equal to sum of white plus two times the red.
W + 2 R = 8 0
W = 8 0 − 2 ∗ 1 2 = 5 6
Back to formula 1
G = 1 6 0 − ( 5 6 + 1 2 ) = 9 2
Please prove the first statement.
Log in to reply
There's no overlapping or whatnot for the first equation.
Rectangle area = White areas + Green areas + Red area
which also is, by algebra
Green areas = Rectangle area - White areas - Red area
"we know that the sum area of the two triangles afc and bfe equal to the half of the rectangle area"
Why do we know this? It's not immediately obvious. One way of looking at this is that the area of ebf is the same as the area of eaf (because the area of a triangle is half base times height) and therefore the area of afc and bfe is equal to the area of aec
Log in to reply
That's really simple. Triangles area = 0 . 5 ∗ e f ∗ b c + 0 . 5 ∗ f c ∗ b c = 0 . 5 ∗ ( e f + f c ) ∗ b c = 0 . 5 rectangle area!
We have two overlapping white triangles with their bases side by side.
If we move the top corners of these triangles to the opposite side, they no longer overlap and the green area now has area 1 / 2 ∗ h ∗ b = 80.
So in the original situation the area of the green part is 80 plus the overlap of the white triangles, which is the red part.
So the area of the green part is 92.
Great Solution, that is exactly how I did it :-)
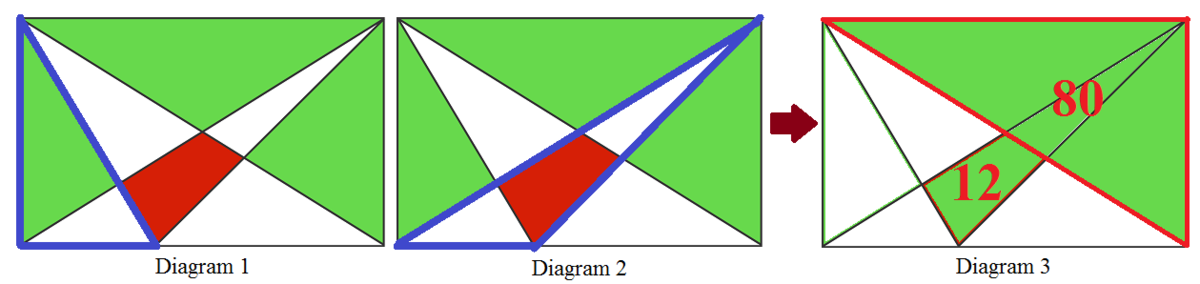 In the Diagram-1 & Diagram-2 the blue marked triangle has equal area. Both blue marked triangle has same base and height. If the common white area removed from the blue marked triangles then green area equal to red and white area. In the Diagram-3, the white and red area changed to the equivalent green area.
In the Diagram-1 & Diagram-2 the blue marked triangle has equal area. Both blue marked triangle has same base and height. If the common white area removed from the blue marked triangles then green area equal to red and white area. In the Diagram-3, the white and red area changed to the equivalent green area.
Therefore, the Area of green shaded region is half of the rectangle plus 12 which is equal to 92.
this is best explanation...i.e., the easiest explanation...thank you!
Note that e + f = f + 1 2 + b , because they are triangles with the same height and base.
This simplifies to b + 1 2 = e , and using the same logic, we can deduce that similarly d + 1 2 = a .
c + b + d + 1 2 = 8 0 , because it is half the rectangle. If we add 12 to both sides:
c + b + 1 2 + d + 1 2 = 9 2 → c + e + a = 9 2
Why is c + d + b +12 one half of the rectangle? Please prove.
Log in to reply
When you combine the shapes c, d, b, and the red shape, they form a large triangle with an area of c + d + b + 12
We can see that the base of the large triangle is the same as the base of the rectangle (top edge of rectangle) and the perpendicular height of the large triangle is equal to the height of the rectangle.
Therefore, area of large triangle = (1/2) * (base of triangle) * (perpendicular height of triangle) = (1/2) * (base of rectangle) * (height of rectangle) = 1/2 * Area of rectangle
Therefore, c + d + b + 12 = 1/2 * Area of rectangle = 80
The area in Green = Area of Rectangle - Area of two obtuse angle triangles + Area in Red (as it is counted twice while subtracting obtuse triangles)
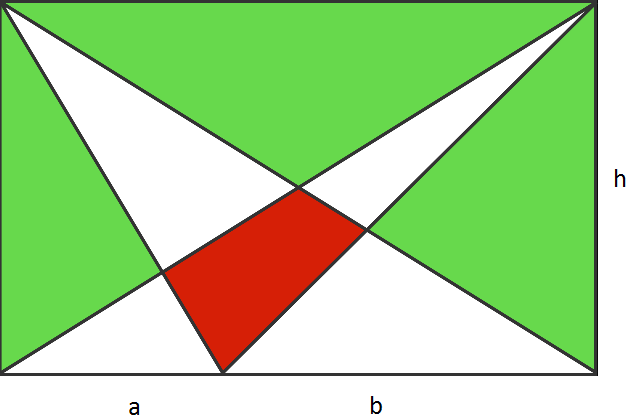
Now Area of two obtuse triangles = 2 1 a h + 2 1 b h = 2 1 (a+b)*h = 2 1 * Area of Rectangle = 2 1 6 0 = 80
so Area in Green = 160 - 80 + 12 = 92
another approach of calculating the areas of the 2 obtuse triangles is to realise that a shear does not change the area. Hence, shearing the left triangle apex to the extreme right shows that the sum of the areas of the triangles is half the rectangle.
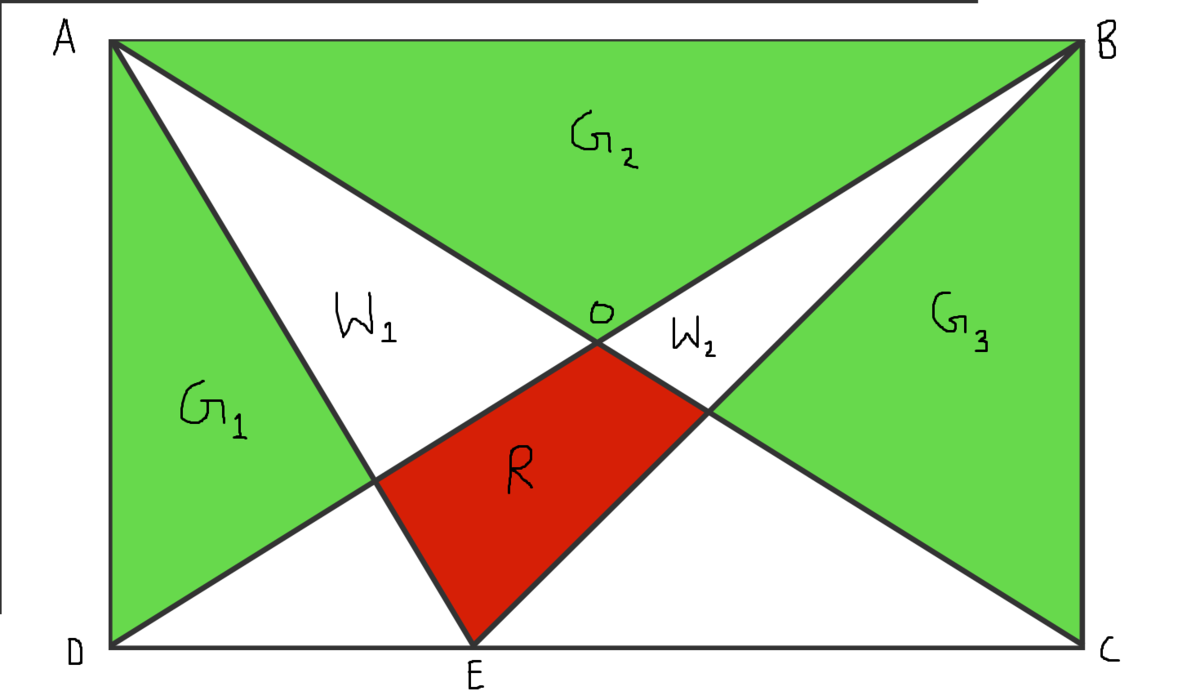 Let
G
1
,
G
2
,
G
3
,
W
1
,
W
2
,
and
R
represents area of respective boundary
.
Let
G
1
,
G
2
,
G
3
,
W
1
,
W
2
,
and
R
represents area of respective boundary
.
We have a r e a ( Δ A B C ) = 1 6 0 / 2 = 8 0 = a r e a ( Δ A B D ) = a r e a ( Δ A B E )
a r e a ( Δ A B D ) + a r e a ( Δ A B C ) − a r e a ( Δ A B E ) = ( G 1 + G 2 + W 1 ) + ( G 2 + G 3 + W 2 ) − ( G 2 + W 1 + W 2 + R )
⇒ 8 0 + 8 0 − 8 0 = G 1 + G 2 + G 3 − R
We are given R = 1 2 ⇒ G 1 + G 2 + G 3 = 8 0 + 1 2 = 9 2
So area in green is equal to 9 2
Please prove your second statement.
Log in to reply
All the three triangles are on the same base AB and between the same parallels (AB and CD). So their bases and heights are equal and so their areas which is equal to 1/2 x base x height = 1/2 x area of rectangle(ABCD) = 1/2 x 160 = 80.
AREA OF A TRIANGLE- 1/2 B * H SO SOME OF THE AREAS OF BOTH TRIANGLES (ECXEPT GREEN AREA) WILL BE- 1/2 ( BASE 1+ BASE 2) H = 1/2 L* B = 80.
AREA OF THE GREEN PART = AREA OF RECTANGLE - AREAS OF BOTH TRIANGLES = 160- (80-12) = 92
I just make 'x and y' axis and assume coordinates and find general area using coordinate geometry . It took me a page to solve this. #difficult method
There are two triangles whose bases together form the length of the rectangle and whose heights are both the width of the rectangle so their combined area if they didn’t overlap would be half of the rectangle. Therefor the remaining space in green is half the area of rectangle plus the red space as subtracting the two triangles from the total would subtract that space twice. This gives 80 + 12 = 92.
This problem is a special case of the more general situation where the vertices of the two top triangles still lie on the top edge of the rectangle, but are not confined to its corners. The answer remains the same.
General problem and solution: Consider a green rectangle. Consider two white triangles whose bases lie next to each other and together fill the bottom edge of the rectangle. The vertices of the triangles lie along the top edge of the rectangle. If the triangles do not overlap anywhere, then the sum of their areas is half the area of the rectangle. The area not covered by the triangles (the area remaining green) is also half the area of the rectangle. If the triangles do overlap then the area covered by the white triangles is reduced by the area of the overlap (the red area) and the green area is correspondingly enlarged.
Green area = half of rectangle area + red triangle overlap area = 160/2 + 12 = 80 + 12 = 92
a + b + 1 2 + 4 0 c + d + 1 2 = 2 1 6 0 . . . ( 1 ) = 4 1 6 0 . . . ( 2 ) Half the area of the rectangular Quarter the area of the rectangular
( 1 ) + ( 2 ) : a + b + c + d = 5 6 = A white , the area of white region. Therefore, the area of green region is given by:
A green = A rectangle − A white − A red = 1 6 0 − 5 6 − 1 2 = 9 2