This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wooooo, you should post a separate question for that :)
We get
4
0
right angle triangles as depicted above. And we get
4
0
triangles having a side of
1
segment,
3
6
triangles having a side of
2
segments,
3
2
triangles having o side of
3
segments and so on up to
4
triangles having sides as 10 segments. No further counting is possible. Thus the total no. of triangles is
=
4
0
+
4
0
+
3
6
+
3
2
+
.
.
.
+
4
=
4
0
+
4
(
1
0
+
9
+
8
+
.
.
.
+
1
)
=
4
0
+
2
2
0
=
2
6
0
If you start counting triangles you will find 20 triangles in length and 20 triangles in the height therefore it should be 40 because rest of the image are just parallelograms
How did you make this Gif?
Log in to reply
Did this on my phone, arghh my eyes indeed.... @Rohit Ner cool gif👍👍
It took me 15 minutes to make it. I wanted to make a nicer one but lost my patience. :P and posted this incomplete gif.
Log in to reply
No, I mean, what is the process of making this gif? Is there an App for it? Did you use magic? Is there a pre-existing image you have on your computer? Did you use telekinesis?
Log in to reply
@Pi Han Goh
–
Actually I edited each and every image and just compiled it into an online gif maker.
PS
: I wish god gave me the power to use telekinesis.
Log in to reply
@Rohit Ner – Oh cool, do you have a link for the online gif maker?
Log in to reply
@Pi Han Goh – There are plenty like this one .
Log in to reply
@Rohit Ner – Ohhhh I'm always curious to learn it but I couldn't find a site that's super easy to use. I'll give it a try.
Thank you.
By the way, the generalization of the n × n grids is 2 n ( n + 3 ) . In this case, it's n = 1 0 .
Log in to reply
@Pi Han Goh – What about m × n
Log in to reply
@Kyle Finch – IDK, I haven't experimented on that yet. Maybe you should post a question about it. ;)
@Rohit Ner – I do not understand how to to use it , please show it.
Log in to reply
@Raven Herd – Just upload the images in a sequential order as you want them in the gif.
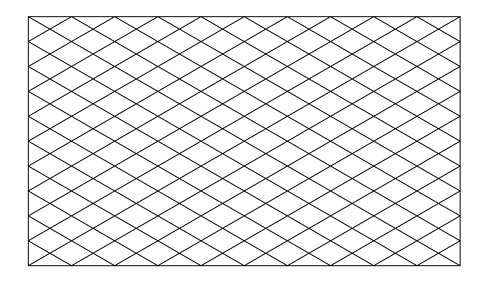
For a m × n rectangle, where m > n , there are:
2 [ ( 2 m + 1 ) + n ] + 2 [ ( 2 n + 1 ) + n ] triangles.
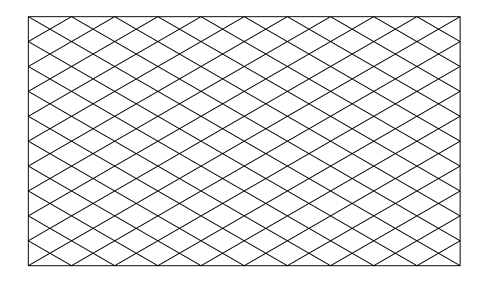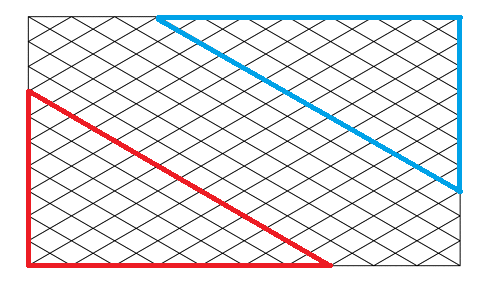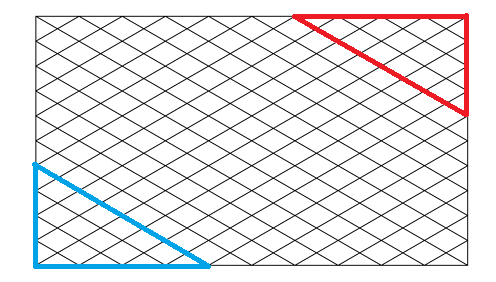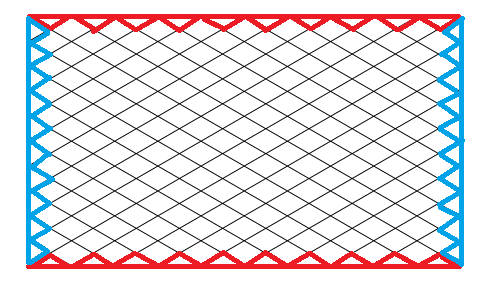
There are two types of triangles in this picture. Right-angled (green) and isosceles (blue).
Number of green triangles formed on every side is n .
Number of blue triangles formed on side m is ( 2 m + 1 ) . This because you can choose two red dots to be the base of your triangle out of ( m + 1 ) dots.
For a square (m=n), formula becomes:
2 m [ m + 3 ]
In this case m = 1 0 , so the answer is 2 6 0 triangles.