Asap
Agatha is at point A , and needs to reach her son Damien at point D as soon as possible. She can swim at a constant rate, and she can also run along the shore at a constant rate (her swimming and running speeds are different).
The diagram shows how long each segment takes her to travel. A direct route A → D takes 61 s, but so does a route of A → B → C → D .
Find the minimum possible amount of time (in seconds) required for Agatha to reach Damien.
Segments
A
B
and
C
D
are perpendicular to the shoreline.
Note: When Agatha swims to and from the shoreline, the angles don't have to be 90 degrees.
The answer is 56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
61 = (7 + 36 + 18)
Log in to reply
in the diagram, the red path uses 56 seconds.
Log in to reply
How did you get the red path??
Log in to reply
@Mark Regnier – By using your red path, you by-passed both above stated options.
Log in to reply
@Mark Regnier – I'm sorry; I don't like the answer because humans neither swim nor run at the speed of light.
Log in to reply
@Mark Regnier – Swimming varies, as does running. (Are we talking with or against or perpendicular or diagonal to the waves/wind???? Or is it completely clam?? // Are we talking swimming or running uphill/ up-altitude or downhill/ down-altitude????) In your problem: Swimming is clearly implied to be the slower of running and swimming. In your answer: You lengthened the the swim distances (and therefore times) (from the 3-sided option). Therefore I can conclude that your path (if we are still talking about swimming and running) should be longer and not shorter in time than you claim. If however, you are switching the problem into a light refraction or reflection problem, I have not calculated that yet.
Log in to reply
@Mark Regnier – this is more of a fun puzzle than real life application. just like every math problem, we assume the speed of swimming and running to be constant, where running is faster than swimming. im sorry this wasnt stated.
the red path is obviously shorter than A->B->C->D path. swimming distance increases a little BUT running distance is shortened by a lot that it actually is faster.
feel free to ask more questions.
@Mark Regnier – u dont need light, it is more elegant but u can do it using calculus if u like.
@Mark Regnier – the "options" is actually given data, u dont have to choose the stated path, u can choose any path as long as it is faster.
@Albert Lau May I know how to know that if light passes through two points. It will do so in the shortest path. Is there way to justify? I don't get the solution you posted including the last line of calculation. Hope you could explain sir,thanks.
Log in to reply
light passes through two points, it will do so in the shortest time , not path (not distance).
this is called fermat's principle. it can be proven using calculus.
there is a proof in wiki: https://en.wikipedia.org/wiki/Snell%27s_law
by the way, the speed ratio has to be calculated before applying snell's law.
hint: construct a perpendicular line from A to CD, call it AE.
hint2: prove that the swim time from A to E is 60 seconds. (pythagoras theorem)
hint3: since AE = BC, prove the speed ratio is 3:5.
@Albert Lau By chances, are you suggesting that the light undergoes internal reflection and the ratio of speed is proportional to ratio of refractive index, hence Snell's Law is applied here?
Log in to reply
no internal reflection needed. in order to apply snell's law, we need to modify our perspective.
we assume the least time path will require a segment of the path to run along the shore. (not always true)
we construct a suitable point P, on BC, we assume the least time path passes through P.
consider a light ray from A to P, either it is a straight line AP or it refracts at the "shoreline", with incidence angle = critical angle, and move east to P.
if BC is wide enough (which is this case), the refraction path is the least time path.
similarly, consider a light from D to P (reversing to-from direction), the least time path is also the refraction path.
i cant upload image in comment section, so feel free to ask any questions.
Log in to reply
@Albert Lau Yeah I am referring to refraction at that critical angle. Thanks a lot for your explanation sir.
Note: A slightly better way to visualize this is to imagine a very thin strip of beach (air) that is sandwiched between 2 blocks of water (glass), and ask what's the shortest time to get from A to the reflected point D.
This way, it's much easier to see that
1) We want an angle
θ
that corresponds to the maximal angle of refraction
2) The light travels (very nearly) horizontally till it exits out to hit point D'.
We can usecalculus to solve this problem without too much complication my dear Abert! It would just bring back the system in a Cartesian frame where it will only be question of distance. With Vswim = 5/3 Vrun f (x) =sqrt(7.^2 Vswim^2+x^2)/Vswim+(3/5) (60 Vswim-(25/7) x)/Vswim+sqrt(324 Vswime^2+(324/49) x^2)/Vswim. Derivative vanishes for x = 21/4 * Vswim==>f(21/4 Vswim)=56.
@ Lounceny Camara - You Are to put a comma right before "my dear Albert." You are addressing him.
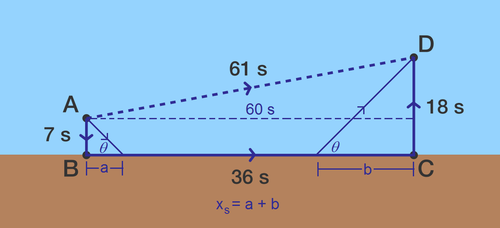
Since Agatha's swimming rate is constant. The distance is directly proportional to time. Therefore, the time taken for a distance of B C is given by t s = 6 1 2 − ( 1 8 − 7 ) 2 = 6 0 s . If the Agatha's swimming speed and running speed are v s and v r respectively, then v s = 6 0 3 6 v r = 5 3 v r .
By Fermat's principle, the shortest path of travel is that taken by light. In this case the beach B C acts like a mirror the swimming path is reflected at the beach with the same angle of incidence and angel of reflection. The total distance swam is then d s = x s 2 + y s 2 , where x s and y s are the distances parallel and perpendicular to B C respectively. Let v r = 1 . Then the time taken by Agatha to run x s distance is x s seconds. And her swimming time is 3 5 x s seconds. We note that she takes 7 + 1 8 = 2 5 s to swimming y s . The time taken running on the beach is 3 6 − x s . Then the total time taken by her to travel from A to D is given by:
t = Running 3 6 − x s + Swimming ( 3 5 x s ) 2 + 2 5 2 = 3 6 − x s + 3 5 x s 2 + 2 2 5
To find t min , d x s d t = − 1 + 3 x s 2 + 2 2 5 5 x s . We note that d x s d t = 0 , when x s = 1 1 . 2 5 and d x s 2 d 2 t > 0 . Therefore, t min = 3 6 − 1 1 . 2 5 + 3 5 1 1 . 2 5 2 + 2 2 5 = 5 6 .
if u use fermat's principle, u can further simplify ur calculation by taking incident angle = critical angle.
Thanks for the answer. There is a small typo in the computation of ts. The sign should be - between the two squares. :)
Assume that her speed in sea is v = 1 m s − 1 , then all we get is A B = 7 m , C D = 1 8 m , A D = 6 1 m , and also by the Pythagorean theorem, we have B C = A D 2 − ( C D − A B ) 2 = 6 1 2 − 1 1 2 = 6 0 ( m ) , so her speed on the land is v ′ = 3 6 6 0 = 3 5 m s − 1 .
Thus, assume she is swimming straightly from A to a point X lies between B C , and let B X = x . Then she running from X to Y which is a point between B C but nearer to C , then also let C Y = y . After she reached point Y , she then changes her direction to point D and swimming straight until she gets to her son.
This all-time process cost a time T , and it can be expressed as T = 1 m s − 1 x 2 + 4 9 m + 3 5 m s − 1 ( 6 0 − x − y ) m + 1 m s − 1 y 2 + 3 2 4 m which then simplify to T = x 2 + 4 9 + y 2 + 3 2 4 + 3 6 − 5 3 x − 5 3 y Because the variable x and y can change independently. So we can let S 1 = x 2 + 4 9 − 5 3 x , and S 2 = y 2 + 3 2 4 − 5 3 y then T = S 1 + S 2 + 3 6 .
This is a small research on this kind of minimum,
So the minimum of S 1 will be 7 1 − 2 5 9 = 5 2 8 and the minimum of S 2 will be 1 8 1 − 2 5 9 = 5 7 2 .
Finally, we have T m i n = 3 6 + S 1 m i n + S 2 m i n = 3 6 + 5 2 8 + 5 7 2 = 5 6 ( s )
You DON’T have to use Fermat’s principle? Wow!
Log in to reply
Actually, don't know how to utilize it... So just invented by myself.
If you assume two different angles alpha and beta (as two independent variables), express Time as function of these two angles, take two partial derivatives with regards to alpha or beta, you can easily see that alpha equals beta and sin(alpha)=3/5.
Log in to reply
Yes, it can be a solution too, but I tend to write solution without calculus.
Wow Genius
Log in to reply
Thanks! I want to share a non-calculus but algebra solution.
We'll start by finding the length of the shoreline with respect to the rates. Assume Agatha swims at a rate of 1 foot per second. Then by the Pythagorean theorem, the shoreline is 6 0 feet long, and Agatha runs at a rate 5 3 of her swimming speed.
I claim that given a distance of a from the shoreline, a running time of r with respect to swimming time, and a sufficiently long shoreline, the distance required to swim with respect to the shoreline is always 1 − r 2 r a Proof Let the distance swam with respect to the shoreline be x . Then by Pythagorean Theorem, the distance swam is a 2 + x 2 . Let the shoreline then be of length b . Then the distance ran is b − x . Weighting these distances with their rates gives t = a 2 + x 2 + r ( b − x ) d x d t = a 2 + x 2 x − r = 0 x 2 = r 2 ( a 2 + x 2 ) x 2 ( 1 − r 2 ) = r 2 a 2 x = 1 − r 2 r a Which completes the proof.
Now, plugging in our values then gives the horizontal distances at the beginning and end, which turns out to be x a = 4 2 1 , x b = 2 2 7 And so the optimal time is t = 4 9 + ( 4 2 1 ) 2 + 5 3 ⋅ ( 6 0 − 4 2 1 − 2 2 7 ) + 3 2 4 + ( 2 2 7 ) 2 = 4 3 5 + 4 9 9 + 4 9 0 = 4 2 2 4 = 5 6
If the angles she makes with the line perpendicular to the shore when she's swimming are P and Q, and her swimming speed is x (so her running speed is 5x/3), then the time taken = (7x secP + 18x secQ)/x + (36 - 7x tanP - 18x tanQ)/(5x/3) = 7secP - 4.2tanP + 18secQ - 10.8tanQ + 36. Differentiate w.r.t. P gives 7secP.tanP - 4.2 sec^2 P = 0 when sin P = 3/5. Similarly sin Q = 3/5, so total time is (7 + 18).5/4 - (4.2 + 10.8).3/4 + 36 = 56. Not very elegant, but you could hardly call it messy.
One could easily find that v b e a c h v w a t e r = 5 3 . Let x be amount of time in seconds spent on the beach. We can manipulate the diagram by hiding the path of the x seconds on the beach as displayed below.

The shortest path on the water is the diagonals of the horizontal distance ( 3 6 − x ) v b e a c h (we and the vertical distance 2 5 v w a t e r in the second diagram, which means the distance traveled in water is ( ( 3 6 − x ) v b e a c h ) 2 + ( 2 5 v w a t e r ) 2 .
The function of time is:
t ( x ) = t w a t e r + t b e a c h
= v w a t e r s w a t e r + x
= v w a t e r ( ( 3 6 − x ) v b e a c h ) 2 + ( 2 5 v w a t e r ) 2 + x
= ( ( 3 6 − x ) v w a t e r v b e a c h ) 2 + ( 2 5 ) 2 + x
= ( 3 5 ( 3 6 − x ) ) 2 + ( 2 5 ) 2 + x
= ( 6 0 − 3 5 x ) 2 + 6 2 5 + x
Solving t ′ ( x ) = 0
( 6 0 − 3 5 x ) 2 + 6 2 5 − 3 5 ( 6 0 − 3 5 x ) + 1 = 0
gives x = 4 9 9 which is a local minima of t ( x )
Therefore, the minimum gives t ( 4 9 9 ) = 5 6 seconds
After you realise that the swimming speed is 3/5 that of the running speed, it's quite easy to prove that there exists and then find the value of an ideal angle of travel. Calculate how much time it takes to swim to and from the shore using this angle, and then add in the time it takes to run between the two shoreline points.
Don't use calculus, it will get messy.
Hint: Fermat's principle. If light passes through 2 points, it chooses the path that does so in the shortest time.
Additional hints: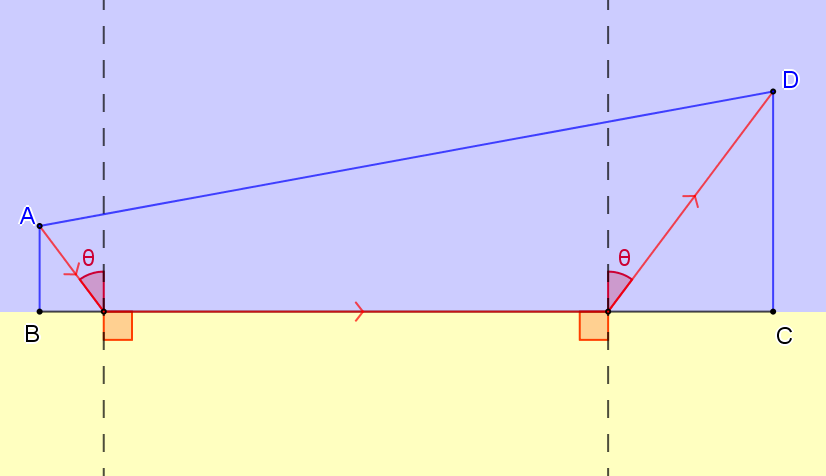 v
run
v
swim
=
5
3
=
sin
9
0
∘
sin
θ
8
.
7
5
+
2
4
.
7
5
+
2
2
.
5
=
5
6
v
run
v
swim
=
5
3
=
sin
9
0
∘
sin
θ
8
.
7
5
+
2
4
.
7
5
+
2
2
.
5
=
5
6