Astonishing result
i = 1 ∑ ∞ j = 1 ∑ ∞ k = 1 ∑ ∞ ( i j k ) 2 1 = b π a ,
where a and b are integers. Find a b .
The answer is 36.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It's times like this that keeping basel series in mind helps a lot. By the way, this should be a level 3 problem at most.
Log in to reply
It is now level 3 :) Give things time to settle down.
Log in to reply
Now back to level 4
Log in to reply
@Figel Ilham – Yea, I blame that on me placing it in my "Calvin's Picks" set, which generated a lot of interest in the problem, while lowering the correct rate.
It might look at first sight a huge mind boggling problem but if you have Basel's series in mind the problem may be solved at a sight. The problem is:- i = 1 ∑ ∞ j = 1 ∑ ∞ k = 1 ∑ ∞ ( i j k ) 2 1 = b π a We can take i and j out of the first summation as being constant for summation over first symbol. = i = 1 ∑ ∞ j = 1 ∑ ∞ ( i j ) 2 1 k = 1 ∑ ∞ k 2 1 From basel's formula:- i = 1 ∑ ∞ k 2 1 = 6 π 2 So our summation becomes:- = i = 1 ∑ ∞ j = 1 ∑ ∞ ( i j ) 2 1 6 π 2 Repeating the same process 2 more times we get the summation:- = 2 1 6 π 6
why is it astonishing????
Sorry a childish thing , you can see that pi value is nearly equal to 3 and here it is raise to 6 , and 6 3 is 216 which we get as result in the denominator
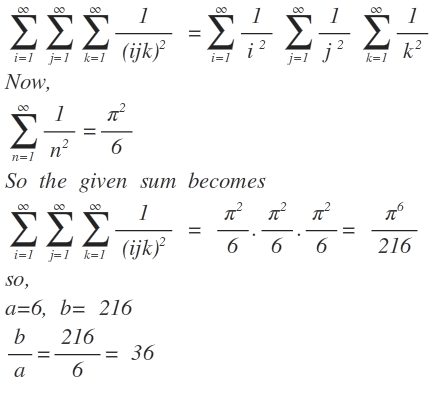
i , j , k can be summed independently.
The summation corresponding to each of them is just
ζ ( 2 ) = 6 π 2
Thus, the required expression is just
( ζ ( 2 ) ) 3 .
Thus, b = 2 1 6 and a = 6 .