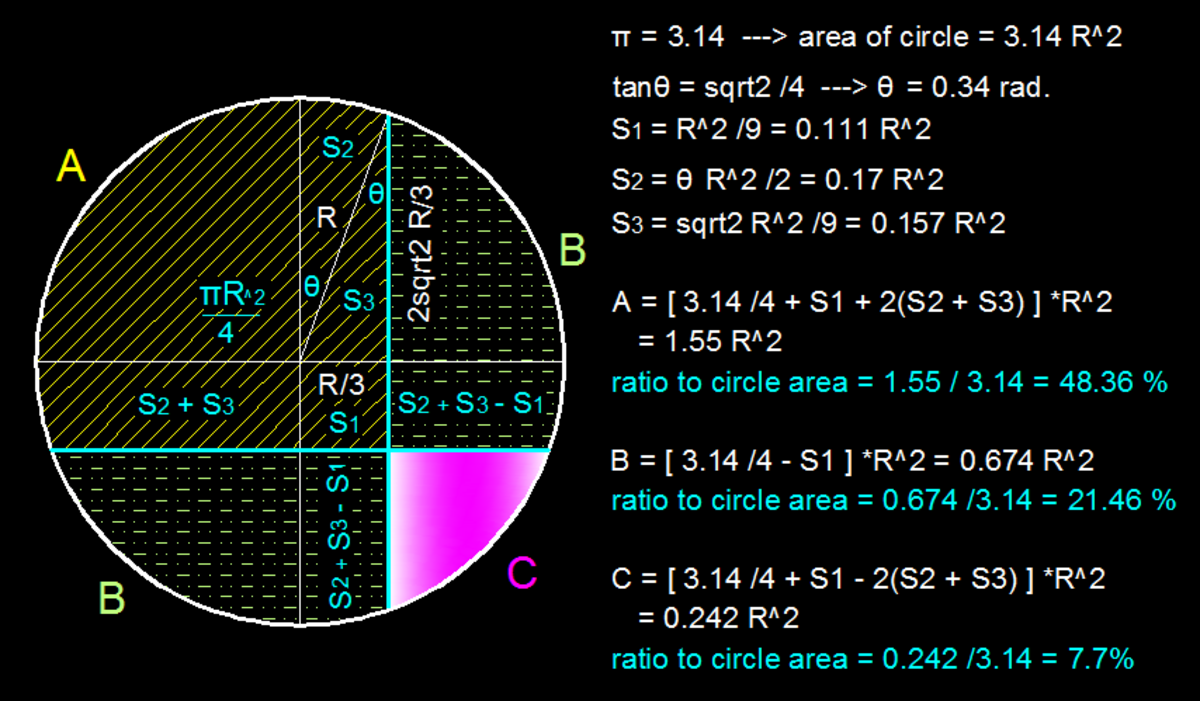
Asymmetric pizza cut

Let's compute the area of the large slice on the top left, assuming unit radius, using only basic circle geometry (draw radii to the points where the cuts intersect the circle in the first and third quadrants):

(quarter circle) + (two sectors subtending an angle of $\arcsin(1/3))$ + (two triangles) + (a square)

$=\frac{\pi}{4}+\arcsin(1/3)+\frac{2\sqrt{2}}{9}+\frac{1}{9}\approx 1.55$

Expressed as a proportion of the total area, $\pi$ , this is about $\boxed{49.4\%}$ .

Happy "Pi Day" to our Comrades in the USA!

PS: If the cuts were to intersect the diameter in a 99:1 ratio, this would be a good illustration on how the pie is distributed in the USA today ;)

Edit: See @ahmad saad ' s excellent illustation

Calculating the exact percentages is challenging; see other solutions. However, it is not too difficult to pick the correct answer from the list given here. The trick is to construct a not-quite-circular pizza with the same area:

Each green section is one-quarter of a circle or an ellipse.

Suppose that the radius of the (original) pizza is 3, so that its total area is $9\pi$ . The pieces of the green distorted pizza then have areas $4\pi$ , $2\pi$ (twice), and $\pi$ , respectively; their total is $9\pi$ as with the original pizza, and the corresponding percentages are $44.4\%, 22.2\%, 11.1\%$ (one of the incorrect options).

Now simply observe that the smallest piece of our original pizza is completely covered by the smallest piece of the deformed pizza. Therefore the smallest percentage must be less than $11.1\%$ . The only option for which this is true is $\boxed{49.4\%,\ 21.5\%,\ 7.7\%}$ .