At least there's a diagram
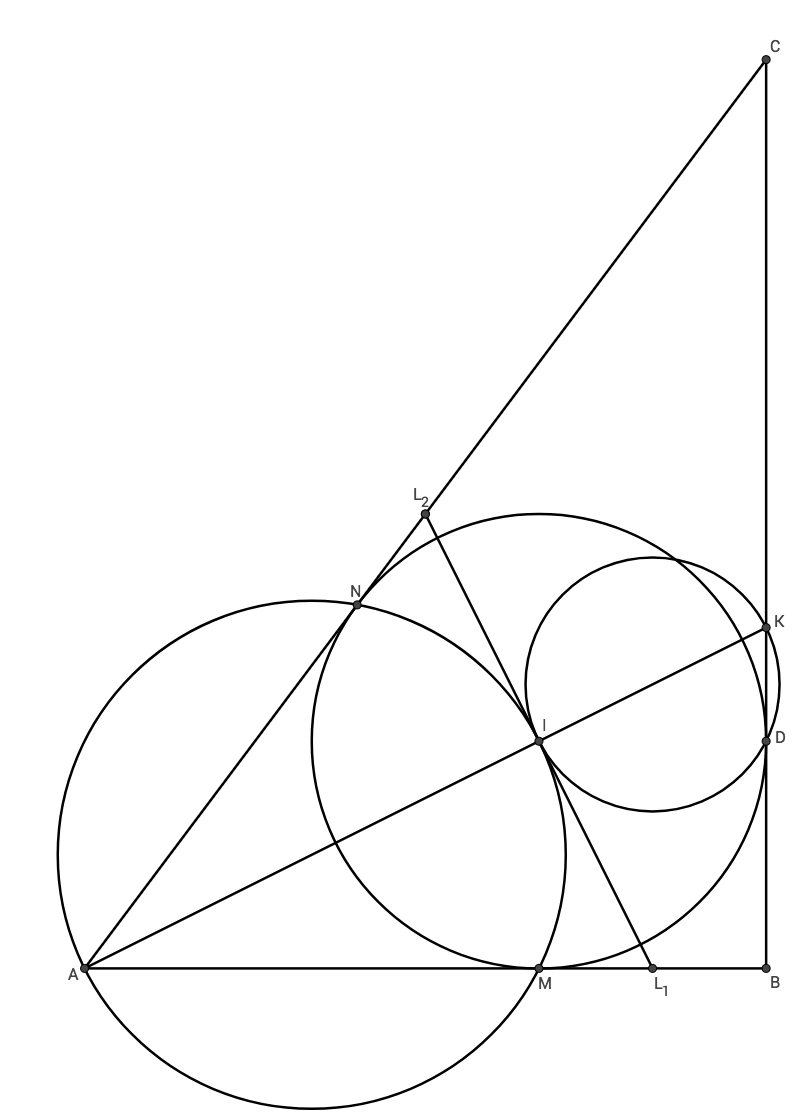
In triangle A B C we have A B = 3 6 , B C = 4 8 , C A = 6 0 . The incircle of A B C is centered at I and touches A B , A C , B C at M , N , D , respectively. Ray A I meets B C at K . The radical axis of the circumcircles of triangles M A N and K I D intersects lines A B and A C at L 1 and L 2 , respectively. If L 1 L 2 = x , compute x 2 .
The answer is 720.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Shrink everything by a factor of 12, and you have a right triangle ABC with sides 3,4,and 5.
∠ B A C = arctan 3 4 = 5 3 . 1 3 ∘
∠ B A I = 2 ∠ B A C = 2 6 . 5 7 ∘
Radius of the incircle = M I = 1 .
A I = sin 2 6 . 5 7 ∘ 1 = 2 . 2 3 6
I L 1 = A I × tan 2 6 , 5 7 ∘ = 1 . 1 1 8
L 1 L 2 = 2 × L 1 = 2 . 2 3 6
Multiply everything by 12 to undo the shrinking at the start
Actual L 1 L 2 = 2 . 2 3 6 × 1 2 = 2 6 . 8 3
Square the result to get final answer = 2 6 . 8 3 2 = 7 2 0
(The answer comes out nicely since I, of course, carry the full precision available rather than just the few decimal places reported.)
How do you know that the answer is EXACTLY 720?
Log in to reply
That came off the calculator. As I said, all I did was carry the available precision. I could have struggled through with the exact figures and all the square roots etc. I did not. So technically speaking I do not know that the figure is absolutely accurate. Whether I know this or not, however, it is the answer I am getting so I give it as the answer. As it obviously came from rounded figures, there is no claim of accuracy involved in doing so.
Log in to reply
You need not shrink or expand or do anything with the figure. The given data is perfect which gives everything in the terms of whole numbers.
Inradius = 1 2 ; A M = 2 4 ; A I = 7 2 0 ; △ A M I ∼ △ A I L 1 = > A I I L 1 = A M I M ⇒ I L 1 = 2 4 1 2 × 7 2 0 ⇒ I L 1 = 2 7 2 0 ⇒ L 1 L 2 = 7 2 0 = > x 2 = 7 2 0
Log in to reply
@Vishwash Kumar Γξω – I knew that I did not need to shrink or expand. I did it to make it easier to follow, with a familiar triangle. I see now that it would have worked better the other way.
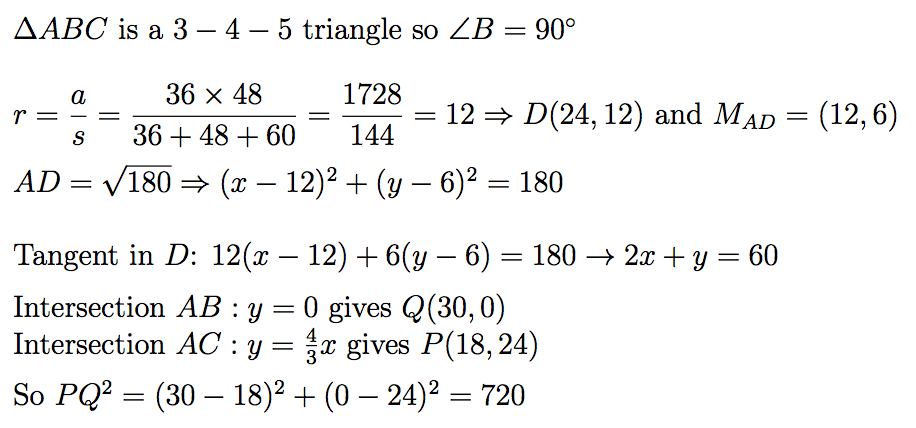
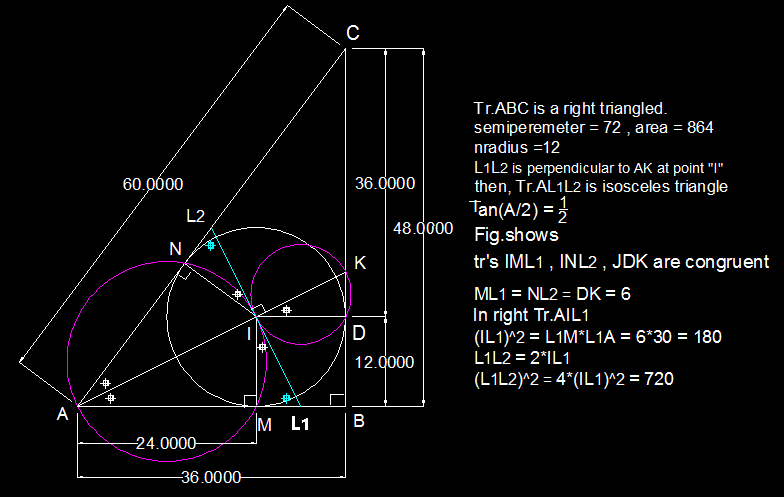
Inradius = 1 2 ; A M = 2 4 ; A I = 7 2 0 ; △ A M I ∼ △ A I L 1 = > A I I L 1 = A M I M ⇒ I L 1 = 2 4 1 2 × 7 2 0 ⇒ I L 1 = 2 7 2 0 ⇒ L 1 L 2 = 7 2 0 = > x 2 = 7 2 0