Attack The White Squares
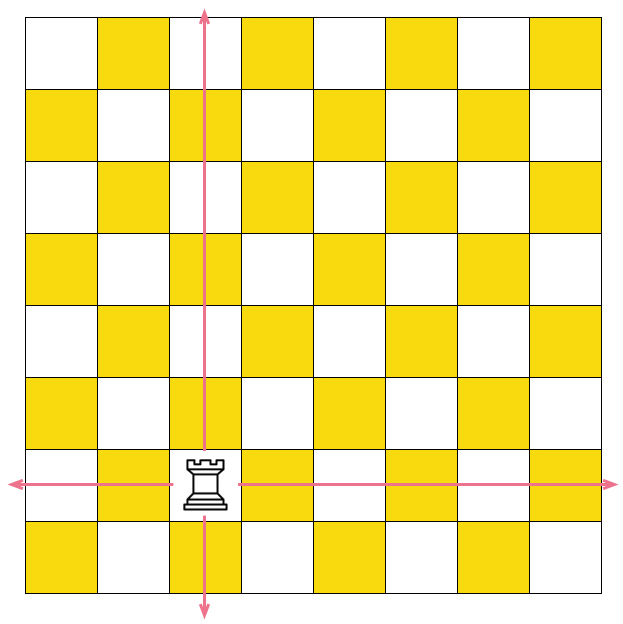
What is the least number of rooks needed to be placed on an 8 × 8 chessboard such that all white squares are attacked by at least one rook?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Good clear explanation.
We have to both show that 4 is a lower bound, and that it can be achieved.
Want to show also , what is the reasoning of how to place them in order to make the understanding complete anyways ?
Log in to reply
There are 32 white squares. There are 4 white squares in each row/column. Thus a rook can only attack 8 white squares, and this can only be done by placing the rooks in black squares and avoiding rooks to attack the same square more than once.
We fix one of the rooks at a1. Now we see that columns b, d, f, h cannot have any rook, since they would attack b1, d1, f1, or h1 as well. This leaves columns c, e, g to have rooks, one each. Similarly, rows 3, 5, 7 will have rooks, one each. As it turns out, placing the remaining three rooks in any way (with the above conditions of one rook per row/column) gives a valid configuration.
Log in to reply
Wow , that's almost exactly how I did it too. However at the point of putting the rooks on black squares it is not completely clear why the rooks have to be there. If they are not , indeed they anyways do not attack all the white squares. Supposing however the problem would state that you should put rooks such that they attack or sit on white squares a configuration wouldn't work.
Because for a configuration of rooks no square should be attacked twice for a rook on a white square R1 taking the white squares of the column/row such that they are not attacked by other rooks means that the other rooks need to be placed such that they attack just black squares of the row/column of R1 which isn't possible. To understand that consider any pair of squares from the row/column of R1 and observe that for any (black , white) pair of squares their column and row will intersect in a black square meaning that the other rooks can't be placed on any black square because then they will attack one white square from the column/row of R1. Thinking in this same terms of pairs of black and white squares for the columns and rows of R1 any pair squares which have the same color will have their columns and rows meet in a white square therefore both the black and the whites meet in white squares in monotonous way by repeating the same rule. Then while it works to place 2 rooks such that they attack just black pairs placing a third on a white square would have to attack one pair of black squares of the column and row of a rook and a pair of white squares of the column and row of the other rook as a result of monotony. This anyways can be interpreted i many ways , as for example a disturbed pattern of parity I think . However this is an interesting thing to note. Anyways , pretty good solution. You should put that stuff about how to place them in it too. Also it is interesting to understand this things as a case study for combinatorial thinking concerning the language (speaking in the terms) of columns and rows. This is also a good way to understand determinism but that's another story. As I said , very good solution. I hope I was clear.
The simple way of expressing what I think you are saying is
Can you show the reasoning of how to place the rooks to satisfy the conditions of the problem.
Log in to reply
Thanks and yes , basically that's it. But just to clarify when I ask for the reasoning , I ask for the understanding by which this reasoning is done anyways.
And , observe that after asking this I add the justification about complete understanding. I just anyways had to put that there to remind generally about the necessary completeness of understanding which should appear in a solution and if I would have asked simpler this question I would still put that justification.
Log in to reply
@A A
–
You are missing my point.
1. Keep your statements simple for others to understand.
2. You have a lot of redundant words that confuse the meaning of your statement.
3. Use proper punctuation to help others understand when there is a (natural) pause.
4. Do not use the word "anyways". It does not mean / is not used in the manner that you are thinking of it. At the most, replace it with "anyway" or "always" or "in any case".
IE Compare
Want to show also , what is the reasoning of how to place them in order to make the understanding complete anyways ?
against
Can you show the reasoning of how to place the rooks to satisfy the conditions of the problem? This would help make my understanding complete
Log in to reply
@Calvin Lin – I agree a little with the first point but I must emphasize also that if I speak too simple I will anyway not express all I feel that must be said. That would make the understanding incomplete and anyway it doesn't help anything.
The words which I use indeed may cover the immediate sense of the proposition. Using them like that (and they are not always redundant) makes people forget and not follow the ideas. I anyway do that because I comment on what I say as a reflexive note. I could not comment but then I would just have to speak just by presenting the immediate reasoning without being reflexive. Yes , anyway I do know that I can comment in the end but that wouldn't work always. I understand anyway what you say but sometimes it isn't possible to do things like that.
Finally you get it with point 3. Indeed , here you think like me. Just when is a natural pause (and you don't have to put it in parenthesis as it is extremely important) I should put a point.
Emmm , ok I will use anyway or indeed even better (but with more words) "in any case". Anyway finally you get something from what I said too. I can't always speak extremely simple and at the same time be explicit enough. If I speak simple it might be either an oversimplification either anyway a very synthetic expression which covers many things but it ambiguous. Anyways , thinking of it the best think I can try is to be a little more synthetic. If being synthetic in expressions can clarify things I will try to do that to make everything easier for anyone.
And about your example. Yes , that is about the weird order in which I put things which indeed makes things a pretty or a lot unclear (what do you prefer ,a lot or a little unclear ?) anyway.
So , I'll try to be a little bit more synthetic and put things in the synthetic order observed. This should deal with the unclear presentation of things. Oh , and it's not just about my understanding. What I meant was that the understanding of anyone can't be complete without those remarks regarding the construction of the configuration.
@Calvin Lin – Btw , Calvin , can you please check a report on the problem "coins game" ? Because I mistake the calculation and I can't change the answer.
I could also change the text such that the problem works for the answer inserted. But then the persons who reasoned correct will not be given credit for their answer anyway.
But how do you cover b2 when you put four rooks on a1, c3, e5 and g7?
Log in to reply
Or D4 or F6 or H8?
Log in to reply
Hey! Editing my last comment! When I had the board drawn out trying to solve it i reversed black and white squares. That's the trick! To attack all white squares you need to place the four rooks on the black squares mentioned in the solution above.
Log in to reply
@Raphaela Cassandra – Ok. I see that d4 is a black square. Thank you for the answer.
b2 is a black square, so it doesn't need to be attacked. (Remember that a1 is a black square.)
Umm, rooks can't attack diagonally
Log in to reply
Yes, rooks can't attack diagonally. What's your concern?
Log in to reply
The attached image (to the problem) is incorrect. I have removed it.
Log in to reply
@Calvin Lin – I think it wasn't meant to represent the attack of a rook. It was a way of representing that rooks should attack all white squares but it was indeed ambiguous anyways.
@Calvin Lin – I interpreted the image as rook needing to attack the white squares (the arrows point to white squares).
Relevant wiki: Chess Puzzles
4 rooks is enough; place them at a1, c3, e5, g7.
4 rooks is necessary. Consider the white diagonal a8-h1; a rook can only attack two of the squares, so we need at least ⌈ 2 8 ⌉ = 4 rooks to attack all eight squares.