Average Equivalent Ring Resistance
There are two colored points (purely abstract entities) situated on a conducting circular ring.
The ring has a total electrical resistance R , which is uniformly distributed over its circumference.
The green point is fixed at a particular location on the ring (the particular location doesn't matter).
The red point traverses over the ring's circumference at a constant angular speed ω , and its location coincides with that of the green point at time t = 0 .
The time-averaged (over an integer number of rotational periods beginning at t = 0 ) equivalent resistance between the two points can be expressed as α R .
Determine the value of α .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
maybe i am wrong.But at first glance, wouldnt averaging over two periods give a different answer?
basically, ∫ 0 ω 2 n π 4 π 2 R ⋅ ( 2 π ω t − ω 2 t 2 )
I = 4 π 2 R ( π ω ω 2 4 n 2 π 2 − 3 n 3 ω 2 ω 3 8 π 3 )
division over ω 2 n π gives 6 R ( 3 n − 2 n 2 ) when averaged over n time periods
Log in to reply
In this case you will also have to consider R 1 and R 2 as R 2 π n θ and R 2 π n 2 π n − θ . Do this and you will see than n cancels out. I've made it over one period for simplicity.
Log in to reply
yes,yes u are right! i overlooked that! thanks :)
Yeah, the trick is that when you're rotating, you can "go forever" and effectively stay in the same place on average. That's why it's advantageous to only try to average over one period. Averaging over more periods requires heightened caution.
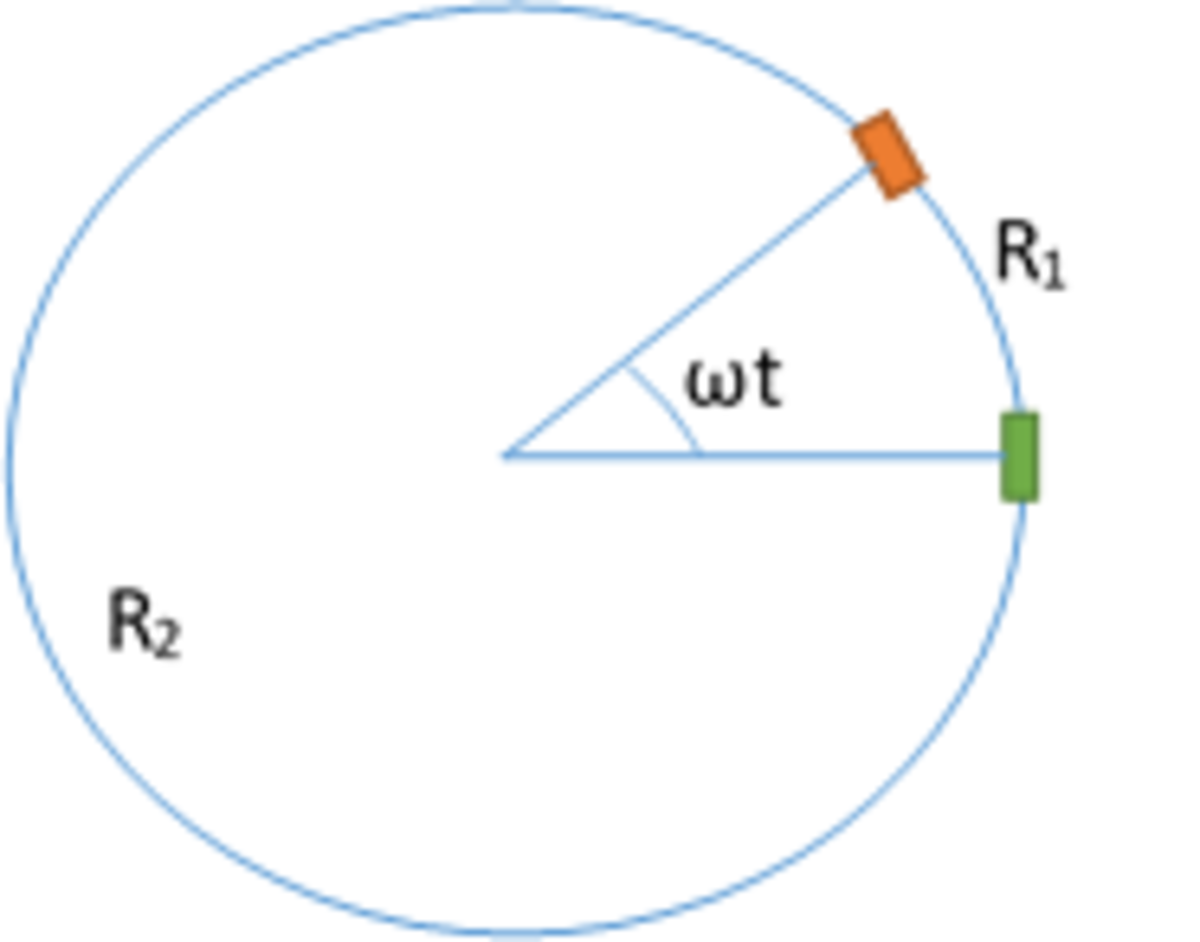
For the first cycle after time t,
R
1
=
2
π
R
ω
t
R
2
=
R
−
R
1
=
2
π
R
(
2
π
−
ω
t
R
e
q
=
R
R
1
R
2
=
4
π
2
R
(
2
π
ω
t
−
ω
2
t
2
)
R
e
q
vs t graph is a parabola for any one of the cycles. If A is the area of one of the parabolas as shown in the diagram, then the average resistance over n complete cycles would be
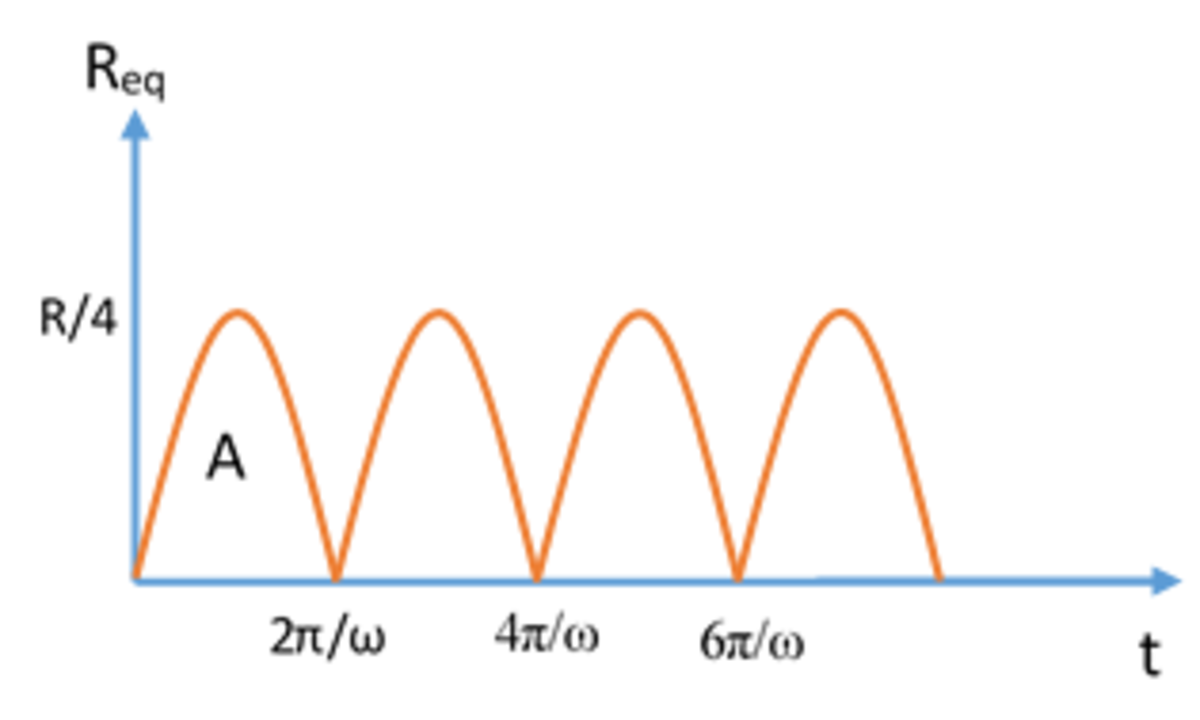 <R> =
t
a
r
e
a
u
n
d
e
r
R
e
q
−
t
g
r
a
p
h
<R> =
t
a
r
e
a
u
n
d
e
r
R
e
q
−
t
g
r
a
p
h
<R> =
ω
n
2
π
n
A
<R> =
ω
2
π
A
A
=
∫
0
ω
2
π
R
e
q
d
t
<R> = R/6
The resistance between the two points is, for one side of the ring:
R 1 = R ⋅ 2 π θ
And, for the other side is:
R 2 = R ⋅ ( 2 π 2 π − θ )
The equivalent resistance is:
R e q = R 1 ∥ R 2 = R 1 + R 2 R 1 ⋅ R 2 = 4 π 2 R ⋅ ( 2 π ω t − ω 2 t 2 )
The time-averaged value will be the integral of R e q over one period divided by one period. First evaluating the integral:
I = ∫ 0 2 π / ω 4 π 2 R ⋅ ( 2 π ω t − ω 2 t 2 ) d t
I = 4 π 2 R ( π ω ω 2 4 π 2 − 3 ω 2 ω 3 8 π 3 )
I = 3 ω R π
The time-averaged value will be:
m = ω 2 π I
m = 6 R
Then, α = 6