Average Magnetic Field
A bounded volume has the following equation
4
x
2
+
2
5
y
2
+
9
z
2
≤
1
.
A charge (
q
=
+
1
0
C
)
is placed at a random postion in this whole volume. Calculate the magnitude of
B
a
v
e
r
a
g
e
magnetic field generated at
(
6
7
,
6
8
,
6
9
)
Details and Assumptions
1
)
ϵ
0
=
1
2
)
μ
0
=
1
The problem is purely original.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Steven Chase
I suggest you to make this type of problem
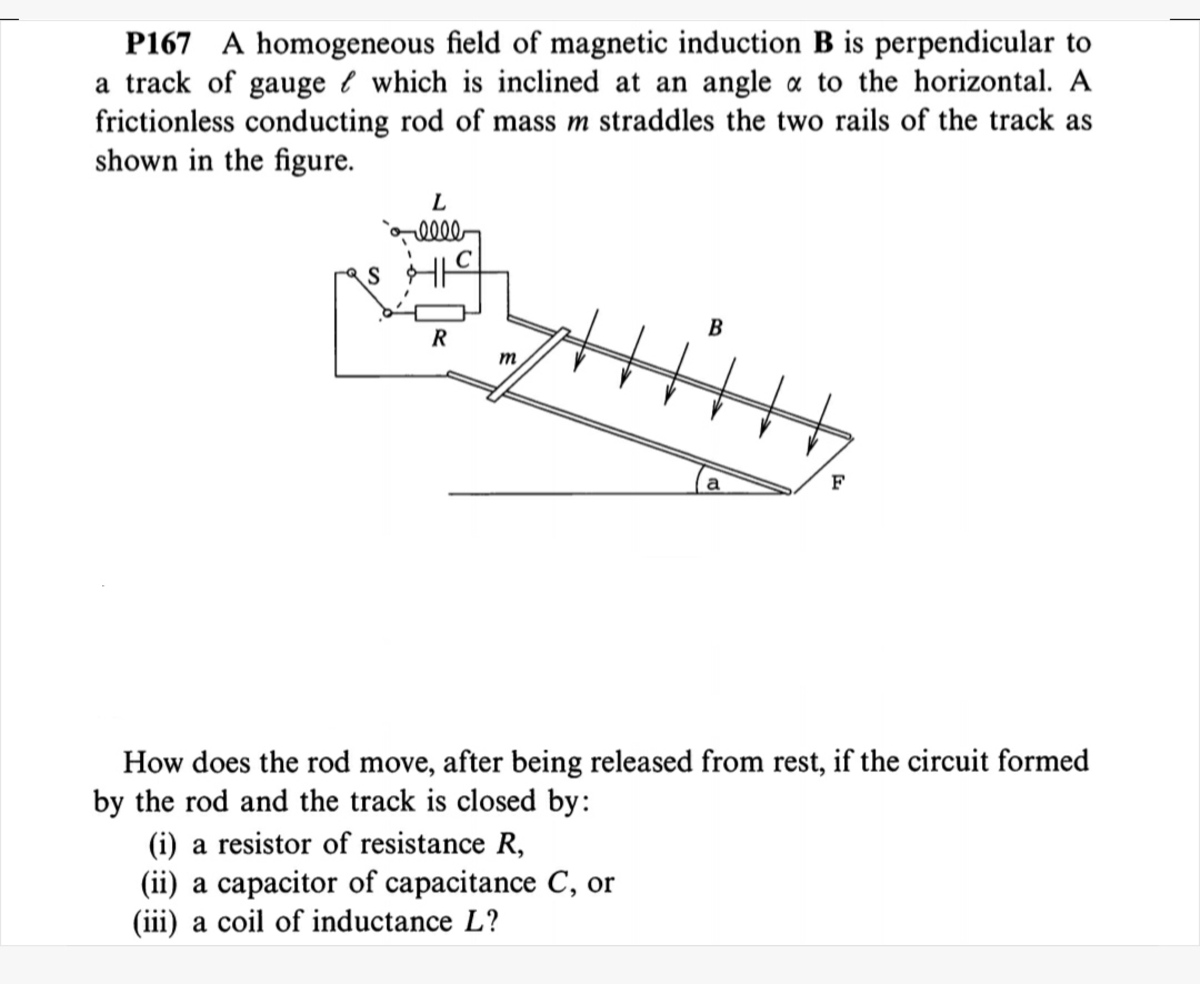
Log in to reply
I'll post one like this soon. The first part will just ask for the steady state speed. The next will ask about dynamics
Log in to reply
@Steven Chase Sir for the new problem I am getting 2 equations B v l − i R − L d t d i = 0 F − B i l = m a
Log in to reply
@A Former Brilliant Member – That looks right
Log in to reply
@Steven Chase – @Steven Chase after simplyfying I am getting 5 v − i = i ˙ 1 0 − 5 i = v ˙
Log in to reply
@A Former Brilliant Member – In steady state, what happens to the time derivatives?
Log in to reply
@Steven Chase – @Steven Chase 0
Log in to reply
@A Former Brilliant Member – Check your numerical substitution also
Log in to reply
@Steven Chase – @Steven Chase I will be very happy if you post a nice follow up. To electromechanics problem. And sorry for the delayed solution
@Steven Chase are you posting part 3 today???
Since the charge is not moving, there is no magnetic field