B is for Brilliant
In each cell of the following 7 × 7 square table, write one of the numbers 1 , 2 , 3 , 4 , 5 , 6 , 7 such that the numbers in each row and each column are distinct. What is the greatest possible value of the sum of the numbers written in the blue squares?
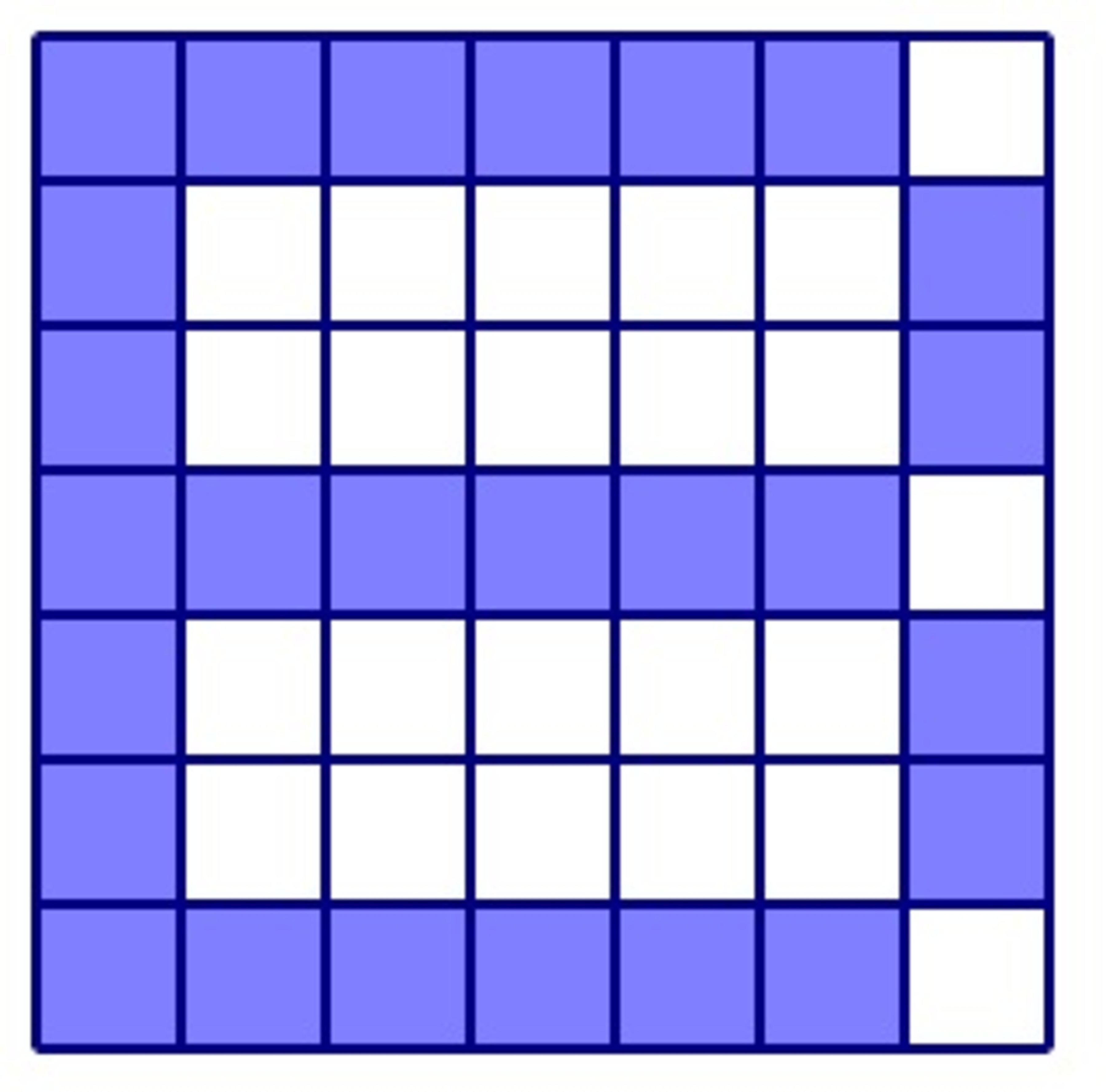
The answer is 122.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I arrived at the same solution! :)
I did the permutation of making max of 5 lines of 7 boxes and den subractd d least possible sum of 3 uncolord boxes frm d sum of 5 lines 7 boxes. Subtractn is req coz d blank boxes make hole in 3 horizontal lines nd 1 vertical line. And sum of blanck boxes must be least, and least sum possible is 1+2+3 and there are 3 boxes so by permutatn we will do like dis. 5x (1+2+3+4+5+6+7) - 3x (1+2+3) = 122
I got 123 the only difference between mine and yours is My A1 is 2, now i did this because that is the spot which is the intersection of 2 columns both blue so it makes sense to make it least so i made a7-1 and a4-4 and a5-3,
Log in to reply
Because of the symmetry in this figure, even if you interchange the values in the position A7, D7, G7 you are supposed to get the same answer. If I can have a look at your solution then may be we can understand the contradiction!!
Why do u need to worry about A4 and A5 ??
Log in to reply
Really no need to worry about A4 and A5. These can have multiple values.
there are 5 line: horizontal up, horizontal middle, horizontal bottom, vertical left, vertical right. each because the line containing permutation 1 to 7, each line sum is (1+2+3+4+5+7) there are 3 intersection 1 in vertical left, and 2 in vertical right (that why there some hole in right). if we want to maximize the sum, the intersection must be as small as possible, each intersection has 3 points: up,middle, and bottom, so the intersection sum is (1+2+3).
answer is: 5x(1+2+3+4+5+6+7)-3x(1+2+3)=5x35-3x6=140-18=122
Nice! I like this argument, except that you'd also have to show that there is an example of arrangement that has this value. As your argument stands, you've proved that the greatest number cannot exceed 122.
For this problem, I am going to refer to the rows as A → G and the columns as 1 → 7 . A group of cells will be notated like in Microsoft Excel; R 1 C 1 : R 2 C 2 refers to all of the cells bounded by rows R 1 and R 2 and columns C 1 and C 2 , inclusive.
There are five major regions of cells that need to be maximized. They are A 1 : G 1 , A 2 : A 6 , D 2 : D 6 , G 2 : G 6 , and B 7 : C 7 ∪ E 7 : F 7 .
Obviously, A 1 : G 1 will contain every digit, but the digits can be arranged to maximize A 2 : A 6 , D 2 : D 6 , and G 2 : G 6 . If A 1 , D 1 , and G 1 are minimized, then their rows' blue cells' sums will be maximized.
Looking at the white entries in column 7 shows that a maximum sum is achieved when the white entries are 1 , 2 , and 3 in some order (similarly, A 1 , D 1 , and G 1 are 1 , 2 , and 3 in a different order). The blue cells in column 7 are 4 , 5 , 6 , and 7 in some order.
Putting in numbers as large as possible to fill rows A , D , and G yields that the maximum sums for A 2 : A 6 , D 2 : D 6 , and G 2 : G 6 are 25 , 24 , and 23 . The sum of A 1 : G 1 is 28 . The sum of the blue cells in column 7 is 22 .
The sum of the entries in the blue entries is 2 5 + 2 4 + 2 3 + 2 8 + 2 2 = 1 2 2 .
An example of a possible board is ↓
2 6 5 4 3 7 1 7 1 4 3 5 2 6 6 4 2 5 1 3 7 3 7 6 1 4 5 2 4 2 3 7 6 1 5 5 3 1 2 7 6 4 1 5 7 6 2 4 3
Using LaTeX, is it possible to make text blue? I would have wanted to do that with the bolded numbers, but I couldn't figure out how.
Log in to reply
To change the color, you can type it as \color{blue} {text}, which gives:
t e x t
Note that you need { } around all the text, otherwise it will only make the first thing blue, as so:
t e x t
Log in to reply
Log in to reply
@Trevor B. – I looked at your Latex code. There wasn't a need to use { } around each letter, since there is only 1 of them in each. For example, 2^3 and 2^{3} both display as 2 3 . However, there is a big difference between 2^34 and 2^{34}, namely 2 3 4 and 2 3 4 .
Think that there are 5 rows or columns blued in total :: (Summing to a total of 28*5 == 140)
Now we are counting the 2 blued corners twice and the 3 non blue squares on the column also twice
We need to substract them and the lowest possible value would be a combination of 1,2,3 with the conditions satisfied..
By this we get the sum as :: (140-(1+2+2)3) == 122
Sum of the numbers in the first blue column is 28.In the first,middle and last rows only one number is missing,let's say 1,2,3 in any order is missing. Individual sums 25,26,27. In the four remaining squares only 4,5,6,7 (in any order) can be there.Total sum 2 8 + 2 7 + 2 6 + 2 5 + 2 2 = 1 2 8 .Now to the three common squares,for the sum to be the greatest those 3 should contain 1,2,3 (in any order). Greatest sum= 1 2 8 − ( 3 + 2 + 1 ) = 1 2 2
Let us consider
A 1 A 2 A 3 A 4 A 5 A 6 A 7
B 1 B 2 B 3 B 4 B 5 B 6 B 7
C 1 C 2 C 3 C 4 C 5 C 6 C 7
D 1 D 2 D 3 D 4 D 5 D 6 D 7
E 1 E 2 E 3 E 4 E 5 E 6 E 7
F 1 F 2 F 3 F 4 F 5 F 6 F 7
G 1 G 2 G 3 G 4 G 5 G 6 G 7
Now, A7, D7, G7 are white so we will try to minimize them and allocate them 1, 2,3. To maximize the blue B7, C7, E7, F7, we will allocate them 7,6,5,4
Now, to maximize the blue B1, C1, E1, F1, we will allocate them 4,5,6,7.
Now there are many possible ways to fill up the rest of the table,
We just have to allocate the Ath row(1st) with, 3,4,2,7,6,5,1. 4th row (Dth row) with 1,3,7,6,5,4,2. 7th row (Gth row) with 2,7,6,5,4,1,3.
Adding the values we get 1 2 2
The matrix I came up with is
3 4 2 7 6 5 1
4 5 3 1 2 6 7
5 1 4 2 3 7 6
1 3 7 6 5 4 2
6 2 1 4 7 3 5
7 6 5 3 1 2 4
2 7 6 5 4 1 3
"The table can be filled up in many ways, but you will get the same answer."