Badminton
Two players are playing a shortened version of badminton: a 6-point, 3-game match with no deuce. Specifically, in each game, the player who first scores 6 points wins. The winner of the match is the player who first wins 2 out of 3 games.
Is it possible for the loser to have accumulated more points than the winner?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
This is a slight variation on Simpson's Paradox, an important concept in statistics. You can read more about it at our wiki. The first portion is below:
Simpson's paradox occurs when groups of data show one particular trend, but this trend is reversed when the groups are combined together. Understanding and identifying this paradox is important for correctly interpreting data.
For example, you and a friend each do problems on Brilliant, and your friend answers a higher proportion correctly than you on each of two days. Does that mean your friend has answered a higher proportion correctly than you when the two days are combined? Not necessarily!
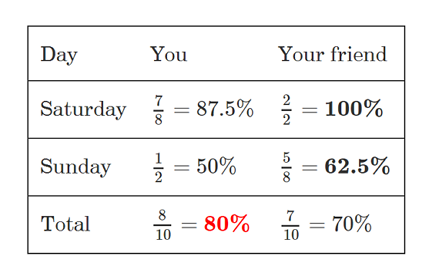
Winner can have a minimum of 12
Log in to reply
Sorry, that was a typo, it has now been edited
But the question says, "The winner of the match is the player who first wins 2 out of 3 games." Then as per the question, it should be NO.
Log in to reply
Please can explain yourself further
Log in to reply
Actually you've already answered in the first sentence itself. Now coming to one part of the question, "The winner of the match is the player who first wins 2 out of 3 games." Please read the word 'first wins'. This means the one who wins first two sets, is automatically having more points. Else the question should be asked like this, "the winner wins any 2 out of 3 games", then the answer would have been the loser gaining more points total.
Log in to reply
@Dibya Jivan Pati – Well then, if that is what you mean, you shouldn't be criticising my solution. My solution is in line with the answer which is marked as correct. Therefore, the sense of ambiguity has been created by the question
@Dibya Jivan Pati – Your explanation is flawed. The winner could have won 6-5 in the first round, lose with 0-6, and won again with 6-5. He is still the one who first wins 2 out of 3 games, but have less point accumulated than the loser.
Log in to reply
@Christopher Boo – I think you did not even try to read my explanation and neither you understood what I'm trying to say...I too agree with what you have commented....whether answer is YES or NO is not issue here...what I'm referring to is the way the question is asked...
Log in to reply
@Dibya Jivan Pati – What's wrong with "first wins 2 out of 3 games"?
P l a y e r A ( w i n n e r ) B ( l o s e r ) G a m e 1 6 5 G a m e 2 0 6 G a m e 3 6 5 T o t a l S c o r e s 1 2 1 6
An extreme case above clearly shows that, yes it is possible that the loser accumulates more points than the winner.
Nice! How did you find these values?
Log in to reply
Just consider the maximum points B (the loser) gets if he loses and wins.
Let
- x denote the winner's score
- y denote the loser's score
Either 2 games are completed from the start or 3 games are completed from the start.
Case 1: If the winner were to win 2 games in the row from the beginning, then it is immediate that the winner earns more than the loser.
Case 2: Otherwise, 3 games are completed. To prove that the loser can earn more points for this case, let's take a look at the bounds.
For loser, since he wins either first or second game, then he earns 6 points. It is then clear that for him to lose two games, the bounds are between 0 and 5 . In this case, 6 ≤ y ≤ 6 + 2 ⋅ 5 , which is 6 ≤ y ≤ 1 6 . So since the winner's minimum bound is 1 2 points (that is, x ≥ 1 2 ), then it is possible that 1 2 ≤ x < y ≤ 1 6 .
We have proven that loser can earn more points than winner .
How did you combine: 12 <= x and 6 <= y >= 16 ? This doesn't seem possible to combine into a single inequality statement since 6 < 12
Log in to reply
The 1 2 comes from the minimum bound of the winner's score without having to make some point in the losing one. Visualize that as setting the bound for the loser's and ask yourself: When is it possible for the loser to earn more points than the winner?
If the winner's bound is x ≥ 1 2 , and the loser's bound is 6 ≤ y ≤ 1 6 , how can we answer the question by comparison? :)
It is possible when the sets won by the loser are with large margin, but loses more no of sets the the winner with a small margin. Since it is asked is it possible, a single example is enough to prove it possible. Consider the scorecard: (6-5,1-6, 6-5). Here player 1 won more no of games than player 2, but with smaller margin, while the game which player 2 won is by a large margin. In this case the total points won by player 1 is 13 against 16 by player 2, still wins the match 2-1 sets.
it is possible in these ways:
3 games= 18 points
as the winner win 2 out of 3 games, he easily scores 6 + 6 = 1 2 points.
so, the looser has to score more then 12 points.
if he(looser) win a match by 6-0 and scores at least 4 points in the lost games, his total point is= 6 + 4 + 4 = 1 4 more than the winner.
again,if he(looser) win a match by 6-0 and scores at least 7(3+4) points in the lost games,his total point is = 6 + 7 = 1 3 more than the winner.
as, there is no deuce, he(looser) can lost a match by 6-5. in this case,he has already scored 10 points in the lost games.then if he wins a game by 6-3 he has scored 16 points where the total points of the winner will be= 6 + 6 + 3 = 1 5 less than the looser.
so, it is possible in many ways.
Of the 216 possible combinations of scores, 35 of them involve the loser scoring more total points. ~16.2%.
Yes, for if there are 2 matches then the winner has to have won both games meaning he will have at least a 2 point lead. but if 3 games are played both players have to have won a match. say the first game went 6-5 but the second game was 0-6, then the last game could still be a 6-2 win and the loser would have more points than the winner.
The minimum accumulated points the winning player can obtain from a 3-game Win-Win-Loose scenario is 12. (6+6+0=12)
The maximum accumulated points the loosing player can obtain from a 3-game Loose-Loose-Win scenario is 16. (5+5+6=16)
Yes, the winning player point accumulation can be less than the loosing player.
Are there still 3 games if the winner has won the first 2?
Relevant wiki: Simpson's Paradox
If the winner wins the first two games, then the winner obviously has more points.
If 3 games are played, the loser must win one of them. The extreme case is that the loser wins 6-0, but loses the other two games 6-5, as these scores maximise the loser's points and minimise the winner's points.
This means that the loser can have a maximum of 16, and the winner a minimum of 12, meaning that YES it is possible.