Balance Mystery

It's easy to do this in 4 weighings, as shown elsewhere. I'll prove this is the minimum.

Each weighing has three possible results, so each weighing will provide us with at most $\log 3$ bits of information. We need to distinguish $4! = 24$ cases, so we need at least $\frac{\log 24}{\log 3} > 2$ weighings, so we need at least 3 weighings...

...is it the lowest bound, though? As it turns out, it isn't.

With 2 weighings, we obtain at most $2 \log 3 = \log 9$ bits of information, so we can distinguish at most 9 cases. Suppose we only need 3 weighings, and consider the first weighing. Upon a result of "equal", "left heavier", and "right heavier", we're left with $a, b, c$ cases each, with $a+b+c = 24$ . But since we only need 3 weighings, after this first weighing, we only need 2 more weighings to finish; so, $a,b,c \le 9$ (otherwise we have too many cases to distinguish with just 2 weighings). Among the possible first weighings, only one allows us to continue:

• Weighing 1 vs 1 will never produce a result of equal, which means 12 cases each for each side being heavier.
• Weighing 2 vs 1 only gives 4 cases of equal (1+2 = 3, 2+1 = 3, 1+3 = 4, or 3+1 = 4), which means 10 cases each for each side being heavier.
• Weighing 3 vs 1 will never produce a result of equal, which means 12 cases each for each side being heavier.
• Weighing 2 vs 2 is the only one that allows us to continue; it splits 8-8-8.

Call the stones A, B, C, D, and suppose our first weighing compares A+B versus C+D. Suppose we get a result of equal. Now we don't have any possible second weighing:

• Weighing 1 vs 1 will still never produce a result of equal, which means 4 cases left each for each side being heavier.
• Weighing 3 vs 1 will always cause the side with the 3 to be heavier. This gives us absolutely no information.
• Weighing 2 vs 2 besides A+B versus C+D will now never produce a result of equal, because the only way to produce equal is if both sides have total weight 5, so the side containing A must also contain B in order to make them equal. Since they are never equal, there are 4 cases for each side being heavier.
• Weighing 2 vs 1, where the 2 comes from the same side, will always say that the 2 is heavier; it has total weight 5, compared to the 1 side that has weight at most 4.
• Weighing 2 vs 1, where the 2 comes from different sides, splits into 2-5-1: Suppose we compare A+C versus B. (Everything else is the same up to renaming.) Then they are equal in the case (A,B,C,D) = (1,4,3,2), (2,3,1,4), and the B is heavier in the case (A,B,C,D) = (1,4,2,3). Everything else makes A+C heavier, and having 5 cases there means we can't finish the job in one more weighing.

This shows that 3 weighings is not enough, thus requiring 4 weighings.

I know no body is going to read this but yet… - this is the solution.
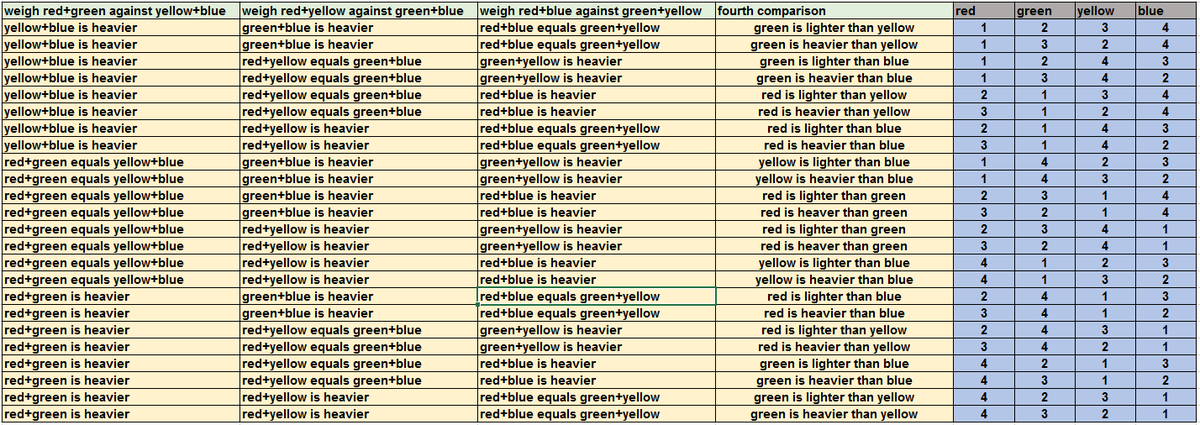
We shall need 4 weighs and I provide the algorithm in the attached picture.
But first let's prove that it's impossible to do this with less weights.
Every weighing action can have 3 outcomes: left is heavier, right is heavier and left equals right.
There are 4! Options for arranging red, green, yellow and blue.
The number of weighing actions should meet the following:
$3^{N}>24$
Which means N=3 or 4 or 5… etc.
I shall show that N=3 is not enough and then I shall show the algorithm for N=4.
The first weigh can be one of the following:
1. One vs. two
2. One vs. three
3. Two vs. two
Let's consider each of these options:

One vs. two – without losing generality let's compare red vs. green+yellow. Let's count the cases where red euquals green+yellow: 3=1+2, 3=2+1, 4=1+3, 4=3+1. It means that we have 4 equal cases. Let's count the number of cases where red is greater than green+yellow: 4>1+2, 4>2+1. It means that we have 2 greater cases. So we are left with 24-4-2=18 cases on which red is less than green+yellow. We are not left with 2 more weighing actions to distinguish between 18 cases. With only 3 outcomes we can distinguish only between 3^2 cases. But we have 18. So we can't.

One vs. Three – No matter what we take – one is always going to be less than adding up 3. Because even in case the one is 4, the other three are 1+2+3 which is 6 and thus 4<6. So after finishing with such a weighing action – we are left with 2 weighing actions to sort out 24. Impossible.

Two vs. two – without losing generality let's compare red+green vs. yellow+blue splits 24 into 8 cases where red+green is less than yellow+blue, 8 cases where they are equal and 8 cases where red+green is more than yellow+blue. We are left with two weights to split 8 cases. No matter what the next weighting action – we shall be left with 4 cases having the same weighing result. The last weighing action cannot distinguish between these 4 because it's it has only 3 outcomes.

So the conclusion is that we can't distinguish between the 24 cases using only 3 weighing actions.

An algorithm for identifying the values of red, green, yellow and blue in 4 weighing actions is illustrate in the image. The first 3 weighing are described on the 3 left most columns. The fourth column weighing action depends on the result of the first three. On the right we can see the conclusion.

Among the $4$ stones, designated as $A$ to $D$ , there are $3$ ways to separate the group into $2$ pairs: $A+B$ & $C+D$ ; $A+C$ & $B+D$ ; $A+D$ & $B+C$ .

From one of these pairings, we know that it will result in equal weighing: $2+3 = 1+4$ .

For generality, suppose $A+B = C+D$ .

We know that the maximum weight rests on either side, and any switch from this equalibrium will result in leveling down towards 4-gram stone: $2+1<3+4$ and $1+3<2+4$ .

Therefore, if we separate the group into $3$ pairings as described for weighing, we will reach one equality and two inequalities. For generality suppose:

$A+B = C+D$ $A+C<B+D$ $B+C<A+D$

Hence, in this case, $D$ is the maximum mass as it favors higher scale, making $C$ the least in order to make the equality true. (If the last inequality has a sign switched to another side, then $B$ will appear twice on the higher scale instead of $D$ .)

That leaves us with $A$ & $B$ unknown, which we can distinguish with just one more weighing.

As a result, we need at least $\boxed{4}$ weighings to know all weights.

Number of equations should be equal to number of unknowns.

We can form equations taking variables as R, G, Y & B.

As there are four variable, at least 4 equations are needed i.e at least 4 trials are needed