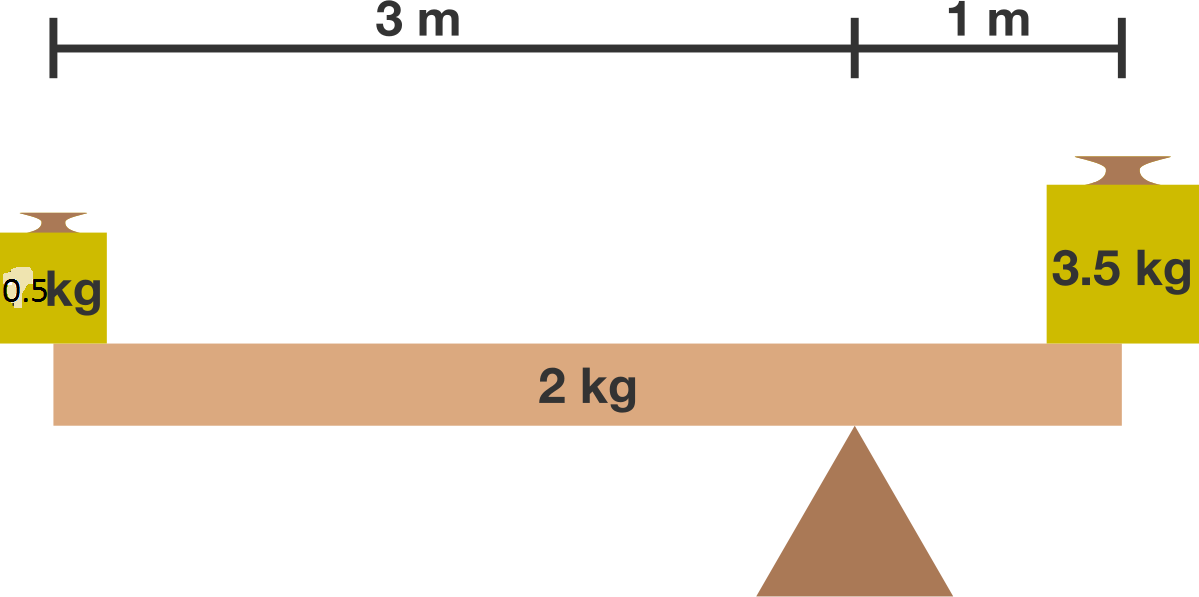
Balance Problem
What mass (in kilograms) on the left side would keep the system in balance?
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Yes! Thank you!
Thanks for the clear solution !
it's not clear to me, you should have used parentheses.
The coefficient of 3 is to due to the 3m distance from fulcrum, correct?
Log in to reply
Yes. That is how moment is defined: distance from the fulcrum × the mass at the spot.
well, said
...But, how did we know that the beam had a uniform mass along its length?
Log in to reply
Of course, it is a reasonable assumption that I and many make to solve this type of problems.
Remember the lever effect ... and knowing that the wood mass effected on 1 meter from the base point.
3 ∗ m + 1 ∗ 2 = 1 ∗ 3 . 5
3 ∗ m = 1 . 5
m = 0 . 5 K g
an interesting tweak: If you ignore the 2m portion of the beam that is perfectly balanced, you now have a 1kg chunk of beam with a center of mass 2m to the left, changing the above equation to 3 m + 2 1 = 1*3.5 (giving, of course, the same answer)
Log in to reply
I like this simplification - I just did it @Chew-Seong Cheong 's way and wish I'd paused for thought first like you have.
thx for explaining
Shouldn't be m = 5/6kg?? 3 ∗ m + ∫ 0 1 . 5 x d x = ∫ 0 0 . 5 x d x + 3 . 5 k g
Log in to reply
for the uniform shape the center of the mass is in the middle and here it is in the middle of the 4 meters beam.
Log in to reply
You're right, sorry! I've calculated that again and got 1.5/3 kg. Also... your solution is nicer :D
and also for your formula you used only the distance and you did not use the mass, so to correct the formula we should multiply by 2 which is the mass of the beam.
3 ∗ m + ∫ 0 1 . 5 2 x d x = ∫ 0 0 . 5 2 x d x + 3 . 5 k g
I need to understand this further. Can you please point to the relevant article on Brilliant or explain just a bit more?
Log in to reply
Relevent article or wiki can be moment of force. :)
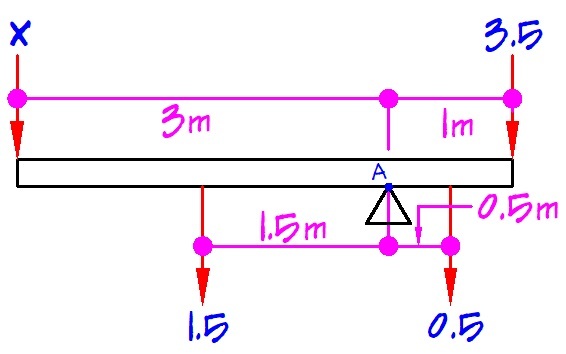
The basic idea is that the mass x length on each side of the pivot must be equal. So the bar gets split in half at the pivot, its two halves each having their own center of mass, and the two weights have a center of mass at the end of the bar. So we use all of this to create the equation:
? kg * 3 m + 1.5 kg * 1.5 m = 0.5 kg * 0.5 m + 3.5 kg * 1 m
All of the kg*m cancel out so we have a simple equation (otherwise we'd have to add converting factors such as 100cm/m):
3x + 2.25 = 0.25 + 3.5
3x = 1.5
x = 0.5
This should be a relevant wiki for it.
kg not *Kg
I Tried to use logical reasoning to try ad solve this problem. I think it works best. I think I should have also measured the plank length since I ignored that. I would rate this problem a 4 because I think all you need is logical reasoning. I found it a little confusing at first so I just decided to keep going so I could make it through.
Question... why did you write, "decimals OK" under the answer bar?
Log in to reply
he did not write it but rather the website itself did that; usually the answers to questions here are integers, but when the answer is not an integer this note appears under the answer bar.
Log in to reply
I feel as if the website should change that to something like, "Decimals are allowed." or "Decimals are OK."
3 m + 1 × 2 = 1 × 3 . 5
⇒ 3 m + 2 = 3 . 5
⇒ 3 m = 3 . 5 − 2
⇒ 3 m = 1 . 5
⇒ m = 0 . 5 kg
wait so the 2 kg are on the left side I thought the whole bar had 2 kg :|
Log in to reply
This equation is similar to my equation, so here's the logic I assume was used: The part of the bar on the right side of the pivot (1 meter long) cancels out part of the bar on the left side, nearest the pivot (1 meter long). So after canceling that out, you're left with 2 meters of bar, the left half of the bar. This part weighs half as much (1 kg). And its center of mass is at 2 m from the pivot. Thus, 1 kg x 2 m.
Log in to reply
The center of mass is at 1m from the pivot, so it's actually 2kg*1m, because the bar is 4m long, so its center of mass is at 2m from its ends, hence at 1m from the pivot
I thought so too!! So I did the whole 2kg / 4 = 0.5 x 3 = 1.5Kg for the left side. And the right side would then have been like 0.5 + 3.5 = 4Kg... then my left was 4Kg - 1.5 = 2.5kg...
Log in to reply
You need to apply the weight at the center of mass. It does not matter if you consider the complete rod at once or breaks it into parts, one left and other to the right of the hinge support.
You forgot to include how far the center of mass acts from the pivot on each side.
That looks right. However the question is flawed. You can't put in 0.5 kg (or 0.5kg, or 500g). It wants a number and 0.5 or 500 are not masses. They need a unit.
Log in to reply
The unit is ''kg'' in the picture.
The unit(kg) is clearly mentioned after the question mark in the figure. So the expected answer should obviously be in kg.
So that the system is in equilibrium, summation of moments at A must equal to zero. We have
∑ M A = 0 ( counter-clockwise moments=clockwise moments )
x ( 3 ) = 1 . 5 ( 1 . 5 ) = 3 . 5 ( 1 ) + 0 . 5 ( 0 . 5 )
3 x + 2 . 2 5 = 3 . 5 + 0 . 2 5
x = 0 . 5 kg answer
Distribution of the self-weigth (2-kg) of the beam:
Note that the 2 k g self-weight of the beam is acting throughout the length of the 4 m beam. First we divide the beam into two, 3 m long and 1 m long. Since the 2 k g is a uniformly distributed load, we must convert it to an equivalent point load (or concentrated load). Observed that the ratio of the lengths is 3 : 1 , so the total is 1 + 3 = 4 . That means that 4 1 ( 2 ) = 0 . 5 k g acts on the right side of the pin support and 4 3 ( 2 ) = 1 . 5 k g acts of the left side of the pin support. The 0 . 5 k g concentrated load must act at the center of the 1 m length beam or 0 . 5 m away from the pin support. The 1 . 5 k g concentrated load must act at the center of the 3 m length beam or 1 . 5 m away from the pin support.
As above figure clearly depicts that the system will have moment about point of pivot(fulcrum). Let the point be denoted as C . For the system to be in equilibrium the moment to the left m L must be equal to the moment to right m R about point C .
If we take a look to left portion net moment produced towards it is the sum of moment produced from left extreme and center point of beam which will lies on the mid point of beam about point C . Let the required mass on the left extreme be k . Then, m L = m R k × l 1 + 2 × l 2 = 3 × l 3 3 k + 1 × 2 = 3 . 5 × 1 k = 0 . 5
This figure mislead the idea 2kg might be weight of beam so this math is wrong
Log in to reply
The weight of beam will be vertically downward from it center. At what point it seems wrong ?
You can ignore the right 1m of wood since it is evenly split. The remaining 1m has a mass of 1kg centered 2m to the left:
3m * ? + 2m * 1kg = 1m * 3.5kg
Or, take the whole mass of the wood centered 1m to the left and get:
3m * ? + 1m * 2kg = 1m * 3.5kg
Either way,
? = 0.5kg
Agreed, the calculation is easy if you ignore the right half of the beam — but note that is 1m either side of the fulcrum — 2m altogether.
This leaves 1kg of beam centred 2m on the left, which offsets 2kg at 1m on the right, leaving 1.5kg at 1m on the right.
This will be balanced by an additional .5 kg at 3m on the left: (1.5kg * 1m) / 3m = .5kg
the torque due to the masses should be balanced.
the weight of the 2kg plank should also be considered.
torque due to plank= ∫ x*(2/4)dx=x^2/4
let the unknown mass be x.
(x 3+3^2/4)=(3.5 1+1^2/4)
9/4+x*3=1/4+3.5
x=0.5kg
The center of mass for the 2 kg isn't really given, but you can pretty much eye ball it at 1 meter.
Torque = Force * Radius
The system is in equilibrium, so the torque on the left must equal the torque on the right.
Torque on the right:
3.5kg * 9.8m/s^2 * 1m = 34.3Nm
Torque on the left:
2kg * 9.8m/s^2 * 1m = 19.6Nm
(Note: we can represent the mass of the beam as a point in its center)
34.3Nm-19.6Nm=14.7Nm
So we need 14.7Nm of torque on the left to bring the system into equilibrium.
14.7Nm = F*(3m)
14.7Nm/3m = 4.9N
To solve for the mass use F=ma which can be rewritten as m=F/a so:
4.9N(9.8m/s^2) = m
m = 0.5kg
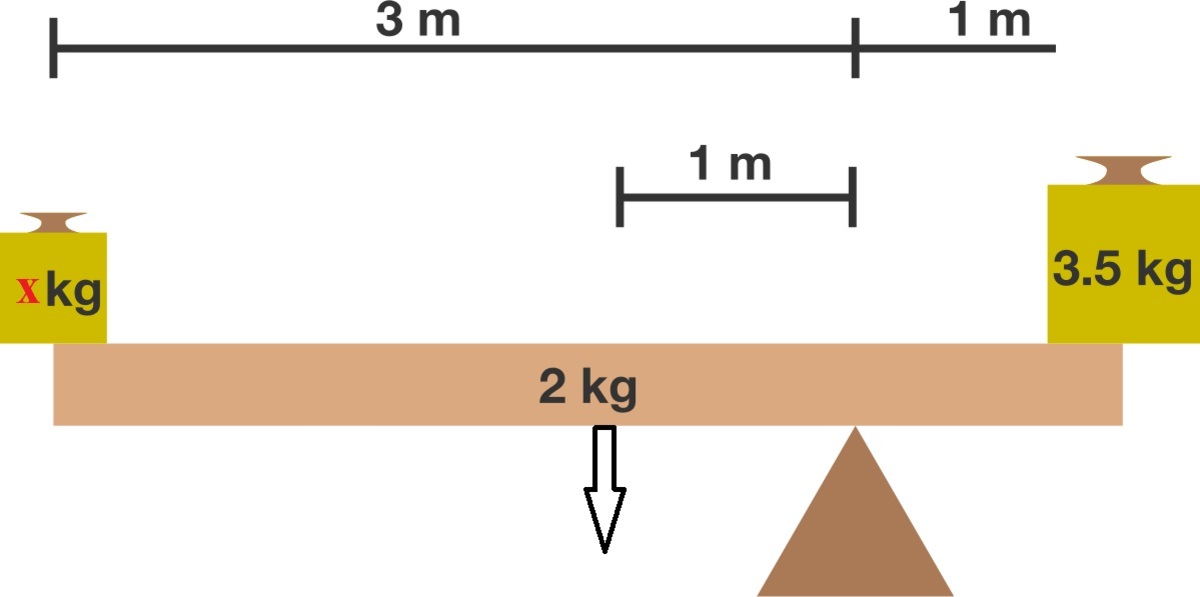
x × 3 + 2 × 1 = 3 . 5 × 1 ⇒ 3 x + 2 = 3 . 5 ⇒ x = 0 . 5
Relevant wiki: Torque - Equilibrium
Split the 2-kg bar in two parts. The part left of the fulcrum has a mass of 1.5 kg and a center of mass 1.5 m to the left of the pivot. The part on the right has a mass of 0.5 kg and with center of mass 0.5 m to the right of the fulcrum. Let the unknown mass of the left be m . Balancing the moments we have:
( 3 × m ) + ( 1 . 5 × 1 . 5 ) 3 m + 2 . 2 5 3 m ⟹ m = ( 0 . 5 × 0 . 5 ) + ( 3 . 5 × 1 ) = 0 . 2 5 + 3 . 5 = 1 . 5 = 0 . 5 kg