Balance the Ball
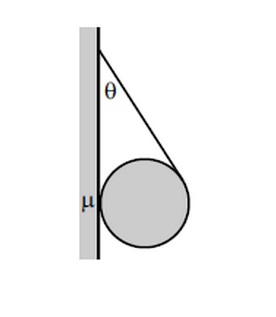A ball is held up by a string, as shown in the figure above with the string tangent to the ball. If the angle between the string and the wall is
θ
, what is the minimum coefficient of static friction between the ball and the wall, if the ball is not to fall?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Perfect..!!
Log in to reply
Thank you sir! :)
Sir If we solve this using Forces balancing then we get μ = tan θ . So there will be 2 answers. Please explain ?
Log in to reply
@Rajdeep Dhingra post your solution and then we will see where is the mistake as the answer must be unique.!!
Log in to reply
@Rohit Gupta – Tcos(theta) *2R=mgR ......balancing moments about point of contact......
and substituting in eq. Tcos(theta) + f = mg.......
we finally obtain u = cot(theta)
Plz explain
How can you balance the forces without calculating the torques (as the ball cannot be considered a particle like object , i.e. the ball cannot be treated like a point mass). Pls post your solution.
Log in to reply
@Abhijeet Verma – I treated it as a point mass. Sorry for the trouble.
Sir I agree with @Rajdeep Dhingra and would be pleased if you take out some time and clear our doubt...thanking you!!
I got that wrong.....oh....but thanks a neat solution.....
The ball is at rest, so τ N e t = 0 . From this, we have F T = F f r .
We also see that the horizontal forces must balance, so F T sin θ = F N . Thus, F f r = μ F T sin θ
From the equation F T = F f r , we have F T = μ F T sin θ . Simplifying, we have μ = sin θ 1 = csc θ
From the figure
As the ball is at rest so net force acting on it is zero.
T s i n θ = N .................(1)
Net torque about CoM should be zero.
So T R = f s R .....................................(2) Here 'R' is the radius of the ball.
As we have to find the minimum value of μ s i.e limiting value of static friction. So
f s = μ s N .............(3)
On solving these equations we get μ s = c o s e c ( θ ) .