Helix
A string winds around a cylindrical pipe, making four complete turns as shown below. The circumference of the pipe is 4 meters and the length of the pipe is 12 meters. How long is the string if the ends of the string meet with the ends of the pipe?

The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
My solution showed the net of the pipe, it didn't show the pipe itself.
Log in to reply
That's fine. But the assignment of the problem make it sound like it is the pipe and the string that are showing. I could solve it, obviously, but I still believe that it is misleading to the general public.
Log in to reply
I will agree with you on the diagram on my problem though, I personally feel like I could have drawn it a little better, but I had a bit of trouble doing so. Thanks for your input.
Can I use your diagram for this problem?
Log in to reply
@Deva Craig – My diagram is far from the best it could be, I too am limited, but you are certainly welcome to it. Thanks for making the change. I think it will make your problem, which is a good one, more popular
If we take the net of the pipe above, we get this diagram:

To find the length of the string, we need to find the value of one of the four blue lines. We'll label the net like this:
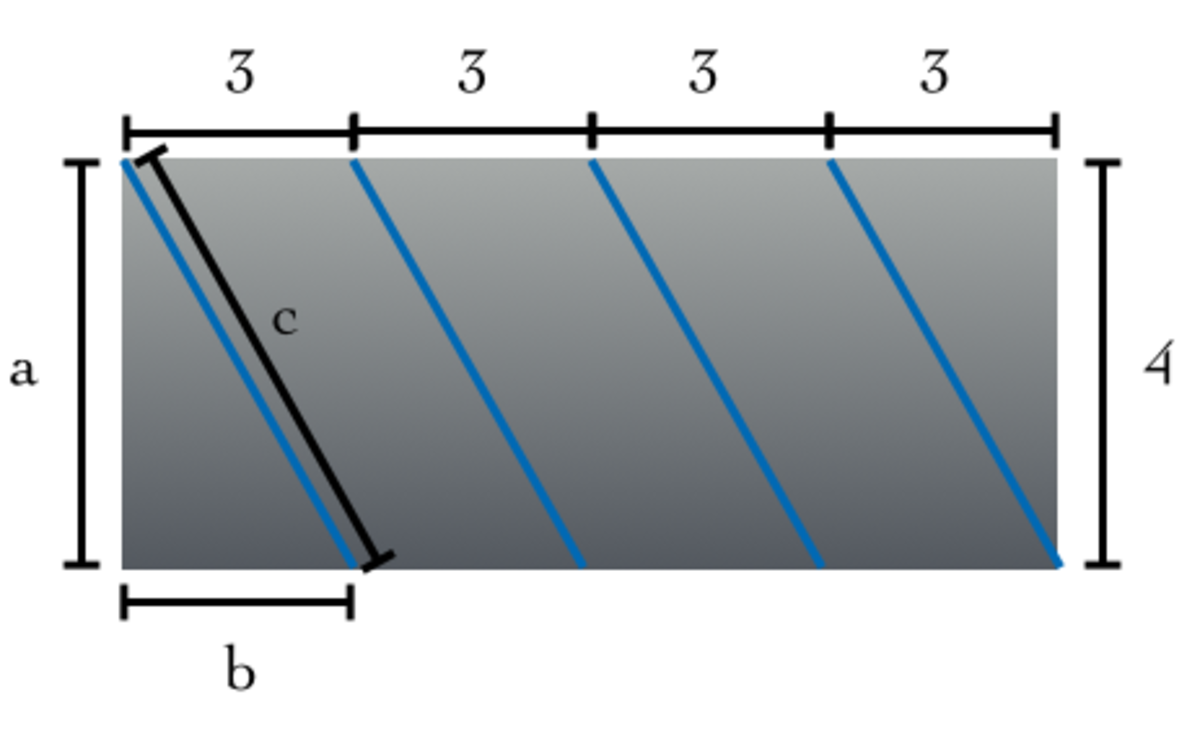
In other words, we must find the value of c. To find c, we can use the Pythagorean Theorem, since we are already given a and b.
a = 4 b = 3
(4) 2 + (3) 2 = c 2
16 + 9 = c 2
25 = c 2
c = 5
Since the circumference of the pipe is 4, to find the length of the string, multiply c by a.
5 * 4 = 2 0
The unwound diagram would look like this: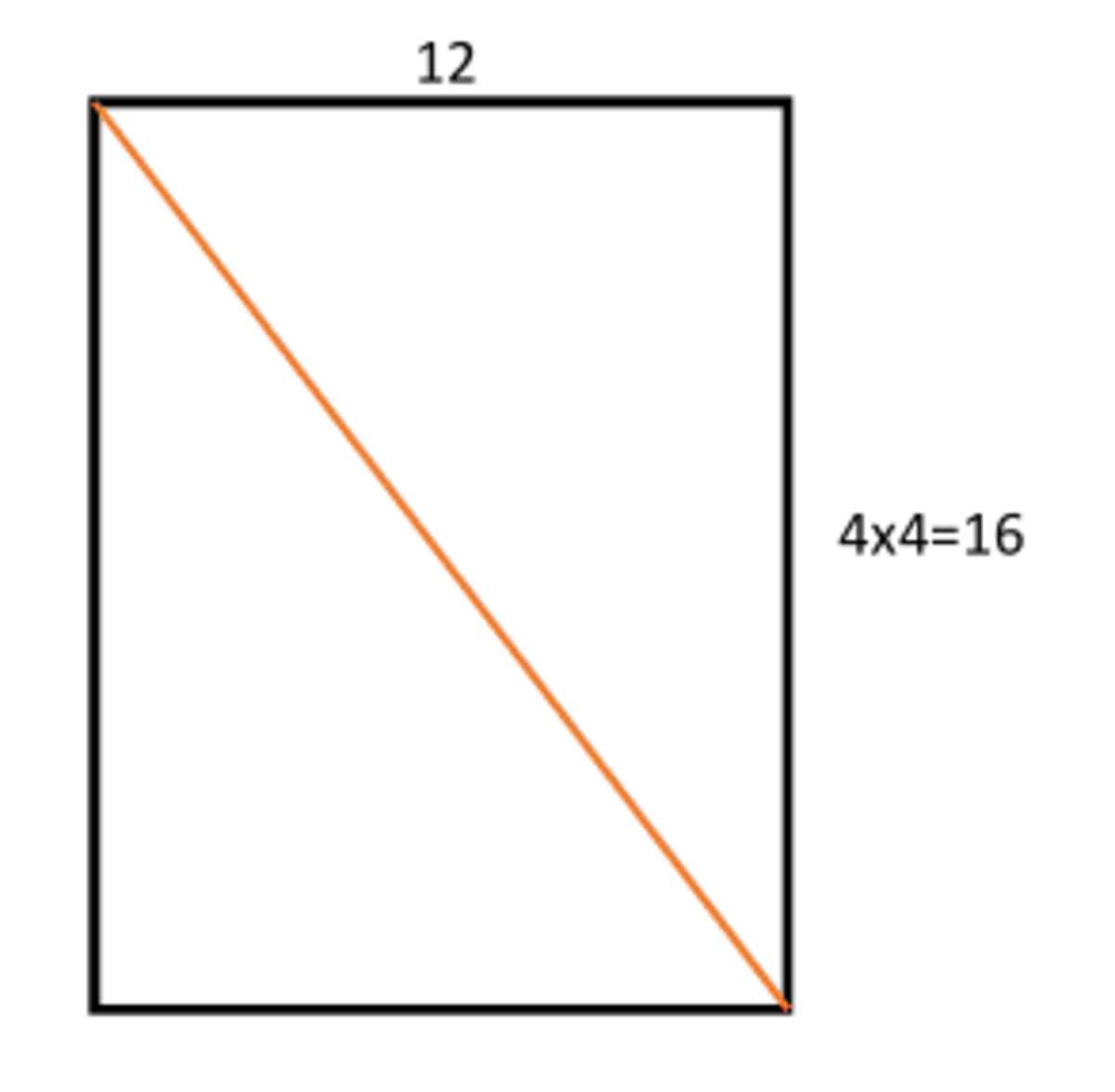 With the answer being
1
2
2
+
1
6
2
=
2
0
With the answer being
1
2
2
+
1
6
2
=
2
0