Bashing Unavailable Bcoz Of Summation!
If sin 6 x = r = 0 ∑ 6 a r cos r x ,
what is a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
setting x=0 would mean that that the equation is an identity......wow..great....nice approach..
because cos(r*0) = 1. nice one sir. i just realized it..
To express c o s n x or s i n n x as a series of multiple angles of cos and sin , we use E u l e r s − r e p r e s e n t a t i o n
c o s ( x ) = 2 e i x + e − i x and s i n ( x ) = 2 i e i x − e − i x
And Expand c o s n x =( 2 e i x + e − i x ) n By Binomial theorem etc.as for the above example
s i n 6 x =( 2 i e i x − e − i x ) 6
2 6 . i 6 1 [ 6 C 0 e 6 i x − 6 C 1 e 5 i x e − i x + 6 C 2 e 4 i x e − 2 i x . . . . . . . . . . . . . . . . . . . . . . . . . ]
= 6 4 − 1 [ 2 c o s ( 6 x ) − 6 ∗ 2 c o s ( 4 x ) + 1 5 ∗ 2 c o s ( 2 x ) − 2 0 ]
3 2 − 1 + 1 6 3 c o s 4 x - 3 2 1 5 c o s 2 x + 8 5
= ∑ r = 0 6 a r . c o s r x
a 0 =5/8
a 1 =0
a 2 =-15/32
a 3 =0
a 4 =3/16
a 5 =0
a 6 =-1/32
sum of all these =
1 6 5
m + n = 2 1
@Calvin Lin ???
Log in to reply
You made a mistake in simplifying 6 4 2 0 , which should be equivalent to 1 6 5 instead of 8 5 . This explains why your answer is off by 8 5 − 1 6 5 = 1 6 5 .
I agree with all the rest of the steps, other accounting for this error.
Note that substituting in x = 0 will give us 0 = a 0 + a 1 + a 2 + a 3 + a 4 + a 5 + a 6 . In particular, we do not need to find the exact values of a i .
I have updated the answer to "1", given the interpretation of 1 0 . I have modified the question, and the answer is now 0.
Log in to reply
I can't understand?? What do you mean to say??
Log in to reply
@Parth Lohomi – Check your arithemtic, specifically this line:
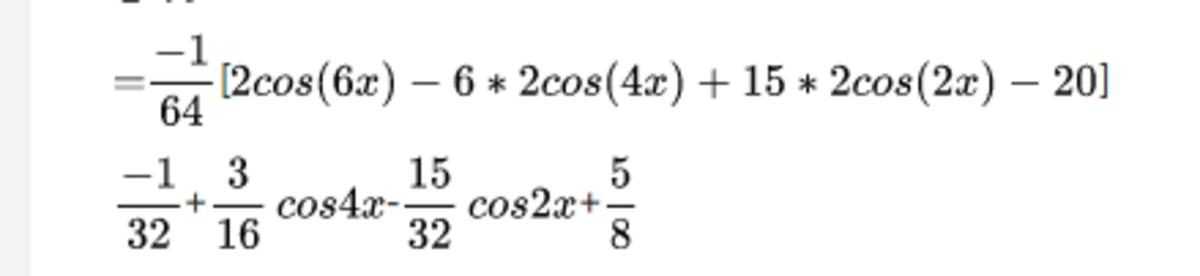
There are 2 errors
1) (minor) You missed out the term
cos
6
x
2) (major) You simplified the constant
6
4
2
0
as
8
5
. Instead, it should be
1
6
5
.
Please fix these errors accordingly.
Log in to reply
Log in to reply
@Parth Lohomi – Once you fix the arithmetic errors, this solution is good.
If I wanted to find the identity, this is the approach that I would take, as it gives the terms almost immediately.
Putting x=0 we get , a1+a2+a3+a4+a5+a6 = 0
Set x=0 . This gives a0+a1+a2+a3+a4+a5+a6 = sin(0)^6=0