Basic Algebra Test
Given that
b + c a + a + c b + a + b c = 1 ,
find the value of
b + c a 2 + a + c b 2 + a + b c 2 .
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
22 solutions
It had 99 votes. I just had to vote it up.
Log in to reply
And now it has just 5 less than a double century.
Log in to reply
Infact 3 xD
And now, It's wayy over 4 centuries. I think this might be the most upvoted solution on Brilliant!
Thoughts? @Calvin Lin
Elegant solution.
Log in to reply
I completely agree with Ajay - a most elegant solution!
Don't you assume that a+b+c is non-zero?
Log in to reply
If a+b+c is zero then the given equation won't be satisfied because (-1)+(-1)+(-1)=-3, not 1.
Log in to reply
Could someone elaborate on this? I just can't get where these -1 -1 -1 come from.
Log in to reply
@Michele Franzoni – If a+b+c=0, then a+b=-c, let x=a+b, x=-c, c=-x, (a+b)/c=x/-x=-1, then do the same things to (a+c)/b and (b+c)/a u will get (-1)+(-1)+(-1)=1, -3=1, which is impossible, so a+b+c must not equal to zero(One year pass I believe u can prove it now😉)
That's exactly what I did. But how did you know you should replace 1 by (a+b+c)/(a+b+c)? I just "guessed" it COULD be the case, but I had no idea until I tried and it actually worked. Going with this "guesslation"/bruteforce could take me forever to solve a problem. So, I really want to know how did you know it was the way to go. Or was it just a guess as well?
Awesome bro :)
if supposed c=0,then get a+b. and a*b,then the expression will be b^2/a+a^2/b then work out the answer -2 ?,???????????
Log in to reply
In that context you can even write c=0/X where X is any real value except 0 itself.
And I was wondering which identity I did not know to solve this problem. Awesome solution!
What if a + b + c = 0 ?
Log in to reply
then it would mean 1=-3
that means 0/0=1
Do you have any triplet (a, b, c) which satisfies this This is true only if a, b, c are complex numbers Not true for any real triplet.
@sean ty I guess your computer is too slow as u "copied" my solution 2 hours after my comment :D
Log in to reply
I didn't mean to. Sorry! Yeah, as they said, The Philippines has a very slow Internet Connection. So I'm really sorry haha. I don't want to be redundant but I really did not intend on 'copying' your solution. We had very similar (If not the same) solutions. :)
Log in to reply
Chill dude.. Atleast the viewers got a nice pictorial solution ;)
Log in to reply
@Sahil Goel – At least no one's angry or anything. I just wanted to avoid any conflict! :D
Log in to reply
@Sean Ty – Sean, you're such an imitator. Pinoy ka talaga!
simple and elegant
very nice solution
that is a great soln
really elegant. mine was a bit lengthy.
Log in to reply
As was mine, Rishi. It was completely counter-intuitive until I saw Sean's beautiful solution!
A pretty solution.
I don't understand what you say. . .
La solution ne convient pas car on nous precise pas que a+b+c est different de 0. Le genre de choses qu'on apprend a l'ecole primaire :)
How did you multiply it?
Log in to reply
( b + c a + a + c b + a + b c ) ( a + b + c ) = b + c a ( a + b + c ) + a + c b ( a + b + c ) + a + b c ( a + b + c ) = b + c a 2 + a ( b + c ) + a + c b 2 + b ( a + c ) + a + b c 2 + c ( a + b ) = b + c a 2 + a + a + c b 2 + b + a + b c 2 + c
this is so dumb. i am in 4th grade and i can do this
Log in to reply
Wait u r in India and 15 years old studding in 4th grade.....or may be 5th now WOW
Will anyone elaborate the second step?
Log in to reply
( b + c a + a + c b + a + b c ) ( a + b + c ) = b + c a ( a + b + c ) + a + c b ( a + b + c ) + a + b c ( a + b + c ) = b + c a 2 + a ( b + c ) + a + c b 2 + b ( a + c ) + a + b c 2 + c ( a + b ) = b + c a 2 + a + a + c b 2 + b + a + b c 2 + c
Am I the only one who thought "If (a, b, c) solves the equation then so does (2a, 2b, 2c) but the value of the second expression would double so if it is unique it must be zero"?
Log in to reply
Beautiful!
Exactly my 'solution' ;-)
Take a=1, b=3/4 and c=5/4 then the first equation holds and the second equation gives 23/14. So the solution is not necessary an integer!!!!
How did you get the first line?
Impressive. The solution is simple. But how did you think of writing 1 as (a+b+c)/(a+b+c) and then multiplying both sides by a+b+c ?
Hey, how do you decide whether to write 1 as (a+b+c)/(a+b+c) and not some other arbitrary thing. But this solution is good.
Then why don't you post it???
This is amazing...
Wow I loved it
Good solution.
Fabulous! This was very innovative.
Wew, this is awesome..
I can solve it in a shorter way....
Log in to reply
I would want to see it!
Prove by solution and not by words.
b + c a 2 + a + c a b + a + b a c = a
b + c b a + a + c b 2 + a + b b c = b
b + c c a + a + c c b + a + b c 2 = c
Add the equations up to get
b + c a 2 + a + c b 2 + a + b c 2 + b + c a ( b + c ) + a + c b ( a + c ) + a + b c ( a + b ) = a + b + c
Therefore b + c a 2 + a + c b 2 + a + b c 2 + a + b + c = a + b + c
So b + c a 2 + a + c b 2 + a + b c 2 = 0
the easiest solution acc. to me...thnx
Log in to reply
You did it the wrong way. let initial expression be X and expression to be found is Y then we are given that X=1. Doing what you did then adding up we get: aX+bX+cX=Y+(a+b+c)
X(a+b+c)=Y+(a+b+c) taking X common
X(a+b+c)-(a+b+c)=Y transposing a+b+c
(a+b+c)(X-1)=Y taking a+b+c common
As we know X=1, we have (X-1)=0 and hence Y=0.
This is the right way.
This is the most intuitive way in my opinion but no the simplest solution.
I also had this solution. This one's better.
ya its easy i can get u
Log in to reply
This is the same as multiplying a + b + c a + b + c .
Log in to reply
For sure it´s the same... But the way that Joseph shows it gets easier to understand the idea of sean Roman...
Log in to reply
@Cleres Cupertino – It is actually how I solved it and realized it is just the same...
easiest solution thanks
( b + c a + a + c b + a + b c ) × ( a + b + c ) = ( b + c a 2 + a + c b 2 + a + b c 2 ) + ( a + b + c ) ⇒ b + c a 2 + a + c b 2 + a + b c 2 = ( a + b + c ) [ ( b + c a + a + c b + a + b c ) − 1 ] = 0
Best! :) ..
Very nice and elegant
Best solution.
Great! =))
Great solution I thought like that only😁
I did it in the most complicated way. Simplifying the equation 1 I got a3+b3+c3+abc=0. I used this in second equation and got the answer 0. :( this solution is very good.
The above two solutions are good but I do not think they are short because each of the 'steps' actually consist of more than one steps thus they may be called easier or more logical but not short.
I used logarithms
thats how I thought about it also :)
First of all, my solution uses that they're asking us for a number. If we have some values a , b , c that satisfy the condition, then − a , − b , − c also satisfy (because b + c a = − b − c − a , and the same to the other fractions. But, in the other fractions, the numbers are sqared, so b + c a 2 = − − b − c ( − a ) 2 , and combining for the three fractions, we have b + c a 2 + a + c b 2 + a + b c 2 = − ( b + c a 2 + a + c b 2 + a + b c 2 ) , which implies b + c a 2 + a + c b 2 + a + b c 2 = 0
Wow!! What a nice solution.... Salute your skills.
a = − a , b = − b , c = − c . The solution presented implies that a = − a , b = − b , c = − c . Also, if an equation contradicts any given condition, it does not imply being equal to zero but indetermination.
Log in to reply
This solution does not assume that a = − a etc., only that the first sum is determined given the second. Given this assumption, it follows that − a , − b and − c give the same first sum as a , b and c , and the rest of the argument follows after that.
Log in to reply
It does. b + c a = − 1 − 1 × b + c a = − b − c − a
The same way that b + c a 2 = − 1 − 1 × b + c a 2 = − b − c − a 2 = − b − c ( − a ) 2 )
I don't see how the solution implies what you say it does. Please explain?
This should be the most highly upvoted solution of this question. Just now, I gave it a +1 and now it has half a century votes.
Very elegant solution!
cool, you have shown the easiest way!
awesome solution ...
Beautiful solution!
The denominators are sums which we don't really like. We turn them into single terms by letting b + c = s , a + c = t , a + b = l , and a + b + c = k . Then we have: s k − s + t k − t + l k − l = 1 , which implies s k + t k + l k = 4 . Then we can write b + c a 2 + a + c b 2 + a + b c 2 = s ( k − s ) 2 + t ( k − t ) 2 + l ( k − l ) 2 = s k 2 + s − 2 k + t k 2 + t − 2 k + l k 2 + l − 2 k = 4 k − 6 k + 2 k = 0 And we are done.
This it was the best of all answers without any doubt!!! Transform a furious denominator in a single number... Awesome!!!
Ya like it to short and easy to understand
thank you so much
My algebra is week. How does s + t + l = 2k. Thanks for your help. P.s. I really like the Idea you use for this problem!
Log in to reply
I see it now. You used the original definitions of s,t,l and k.
Excellent approach
Creative solution :D
By Nesbitt's Inequality, we have b + c a + a + c b + a + b c ≥ 2 3 for all positive real numbers a , b , c .
If a , b , c are all negative, then − a , − b , − c are all positive, then we will arrive at the same equation, which is a contradiction. Hence at least one of a , b , c must be 0 . WLOG set a = 0 . Then we have c b + b c = 1 ⟹ b 2 + c 2 = b c
We want to find c b 2 + b c 2 .
Note that c b 2 + b c 2 = b c b 3 + c 3 = b c ( b + c ) ( b 2 + c 2 − b c )
Since b 2 + c 2 = b c , then b c ( b + c ) ( b 2 + c 2 − b c ) = 0
why cant you have a as positive and b and c as negative or different combinations like that?
Seriously flawed: if (a,b,c) are not all positiv nor all negativ then they are mixed, no need to be 0. In fact, if setting a=0 and assuming real numbers, as you did, then you end up at b/c+c/b=1, which has no solution (look at f(x)=x+1/x ).
L e t x = b + c a , y = a + c b a n d z = a + b c . B y r e w r i t i n g t h e c o n s t r a i n t , w e h a v e x + y + z = 1 S i n c e a = x ( b + c ) , b = y ( a + c ) , c = z ( a + b ) , w e h a v e a + b + c = x ( b + c ) + y ( a + c ) + z ( a + b ) a + b + c = ( a + b + c ) ( x + y + z ) − a x − b y − c z a + b + c = a + b + c − a x − b y − c z a x + b y + c z = 0
Nice solution :)
a + b + c = a + b + c - ax - by - cz How did you get to here? I can't follow from previous step.
x+y+z=1 substitute in previous
In the given equation write 1 as a+b+c/a+b+c and then cross multiply to get the answer ;)
Can you add more details explaining what you did?
Log in to reply
Yeah sure.. 1.Write 1 as a+b+c/a+b+c 2.Take a+b+c of the denominotor to the LHS and multiply with every term. 3.Then split the terms according to the requirements of the question and you will get a^2/b+c + frac b^2/a+c + frac c^2/a+b + frac a(b+c)/b+c +frac b(a+c)/a+c +frac c(a+b)/a+b=a+b+c 4. Cancel the numerator and the denominator in 4th, 5th & 6th term. 5. You will get a^2/b+c + frac b^2/a+c + frac c^2/a+b + a + b + c = a + b + c 6. Now cancel a+b+c from both the sides to get the answer that is zero. ;)
Log in to reply
Please forgive me Sahil, but I wanted to read your solution, so using my beginner skills, I tried to patch up your LaTeX.
Yeah sure..
1.Write 1 as a + b + c a + b + c
2.Take a+b+c of the denominator to the LHS and multiply with every term.
3.Then split the terms according to the requirements of the question and you will get: b + c a 2 + a + c b 2 + a + b c 2 + b + c a ( b + c ) + a + c b ( a + c ) + a + b c ( a + b ) = a + b + c
4.Cancel the numerator and the denominator in 4th, 5th & 6th term.
5.You will get b + c a 2 + a + c b 2 + a + b c 2 + a + b + c = a + b + c
6.Now cancel a+b+c from both the sides to get the answer that is zero. ;)
Interesting :)
I expanded the first part, got a relationship and then expande the second part which was to be calculated and then put the values of the 1st equation to get 0.
Someone please just tell me how to use formatting guide..
To do this, it is not necessary to prove that a + b + c is diferent of zero?
Log in to reply
If that were true, you could deduce that the given sum is equal to -3 instead of 1.
Can we multiply and divide by the same number? What about if the sum equal to zero?
b + c a + a + c b + a + b c = a + b + c a + a + b + c b + a + b + c c so . ∑ a ( b + c 1 − a + b + c 1 ) = 0 .
hence . ∑ ( b + c ) ( a + b + c ) a 2 = 0 .
because a + b + c can't be 0
so ∑ b + c a 2 = 0
Q.E.D
Looking at the solutions given, I came to know how stupid I am.
Here is what I did (not a correct method but interesting):
Take
c
=
0
. Then the equation reduces to
b
a
+
a
b
=
1
, solving this we get
b
a
=
−
w
where
w
is the complex cube root of 1.
Now, if we take
b
=
w
, then
a
=
−
w
2
Substituting these values, the given expression is found to be equal to 0.
I think the least elegant solution would be this.
From b + c a + a + c b + a + b c = 1
we deduce a 3 + b 3 + c 3 + a b c = 0 .
Taking the least common multiplier in the expression
b + c a 2 + a + c b 2 + a + b c 2
and computing the numerator we found it is
( a + b + c ) ( a 3 + b 3 + c 3 + a b c ) = 0 .
That's it.
Let x : = a / ( b + c ) , y : = b / ( c + a ) , z : = c / ( a + b ) , w : = a x + b y + c z , then a + b + c = ( x + y + z ) ( a + b + c ) = w + x ( b + c ) + y ( c + a ) + z ( a + b ) = w + a + b + c , which implies w = 0 .
Let s = a + b + c
∴ s − a a + s − b b + s − c c = 1
Now
s − a a 2 + s − b b 2 + s − c c 2 = s − a a 2 − s a + s a + s − b b 2 − s b + s b + s − c c 2 − s c + s c
= s − a a ( a − s ) + s a + s − b b ( b − s ) + s b + s − c c ( c − s ) + s c
= s − a a ( a − s ) + s − b b ( b − s ) + s − c c ( c − s ) + s ( s − a a + s − b b + s − c c )
= − s + s = 0
The answer is easily obtained without doing the math. Since any solutions for a,b,c will work equally well with 2a,2b,2c, then assuming the question is valid and has an answer, 2(a^2+b^2+c^2) = a^2+b^2+c^2, so the answer must be zero.
I found the least elegant method. I noted that the problem is homogeneous, so a=1 is a possible solution. Substituting a =1 gives us a homogeneous equation in b,c so we can set b=1 as well and solve for c, which turns out to be c= (1+- i rt 7)/2. Using c = (1 + i rt 7)/2 and a=b=1 in the second equation yields 0. Not pretty, but it works. Congratulations to the other solvers who found much nicer solutions!
Its easy to show the implication of the exercise ( if ...=1 holds then 2nd line must =0) and even easier to conclude from homogenous: if it's unique then it must be 0. But no one else addressed the existence of a solution (a,b,c) -> upvoted.
Just as a side note, it is not hard to guess the numerical value, because the given condition on a , b , c is homogeneous.
so i like joseph varghese's solution (simplify the expression a+b+c); Sean Ty's solution isn't bad either, very clever. I personally just solve problems with approaches I don't need to memorize. It's not efficient, but fairly easy to follow.
for this problem it took me a while to find patterns, but eventually after an hour of mulling over it I came across the geometric first step of representing the denominator of the expressions as a box with lengths, height, and widths of (b+c), (a+b), and (a+c); multiplying this out takes a while, but splitting the volume into 8 pieces, and then multiply the original expression out with common denominator, we get (b+c)(a+c)(a+b)=a^2b+ca^2+ab^2+abc+ac^2+abc+bc^2+cb^2=a^3+a^2b+a^2c+abc+ab^2+b^3+abc+cb^2+abc+bc^2+ac^2+c^3; the multiplication is sort of tedious so this isn't really a clever solution, but canceling terms in this expression yields a nice expression 0=a^3+b^3+c^3+abc;
multiplying the question expression out to a common denominator yields a numerator a^4+b^4+c^4+ba^3+ca^3+ab^3+cb^3+bc^3+ac^3+bca^2+acb^2+abc^2=a(a^3+a^2b+a^2c+b^3+c^3+abc+cb^2+bc^2)+b^4+c^4+cb^3+bc^3=a^3b+a^3c+acb^3+abc^2+b^4+c^4+cb^3+bc^3=b(a^3+acb+ac^2+b^3+cb^2+c^3)=b(ac^2+cb^2)+a^3c+c^4=c(abc+b^3+a^3+c^3)=0
brilliant encourages users to find the most efficient solution possible, so this solution probably won't win you the math olympics, but I find value in solving problems with your own wits first and only look at solutions if you'v done all you can; though this again is not efficient because I'm basically reinventing the "wheel" everytime instead of utilizing what my predecessors have to offer.
I'd recommend everybody to not try to reinvent the "wheel", but understanding how the wheel came to be can be important if I want to understand how the past differs from the present, and history...and so on so forth.
enough ranting anyways, I'd just add that I've finally realized what I've done wrong in the past. If everyone went about life like me, the world might still be in the dark ages lol
Rearranging the original equation:
b + c a = 1 − a + c b − a + b c
a + c b = 1 − b + c a − a + b c
a + b c = 1 − b + c a − a + c b
Substituting into the second equation:
a ( 1 − a + c b − a + b c ) + b ( 1 − b + c a − a + b c ) + c ( 1 − b + c a − a + c b )
Distributing:
= a − a + c a b − a + b a c + b − b + c b a − a + b b c + c − b + c a c − a + c b c
Collecting terms:
= a + b + c − a + c b ( a + c ) − a + b c ( a + b ) − b + c a ( b + c )
Cancelling:
= a + b + c − a − b − c
= 0
Again, Mathematica does the trick:
Simplify[ a^2/(b+c)+b^2/(a+c)+c^2/(a+b) /. Solve[a/(b+c)+b/(a+c)+c/(a+b)==1,{a}] ]
Gives
{0,0,0}
As the three possible solutions.
Where r you multiplying with a+b+c on both the sides.
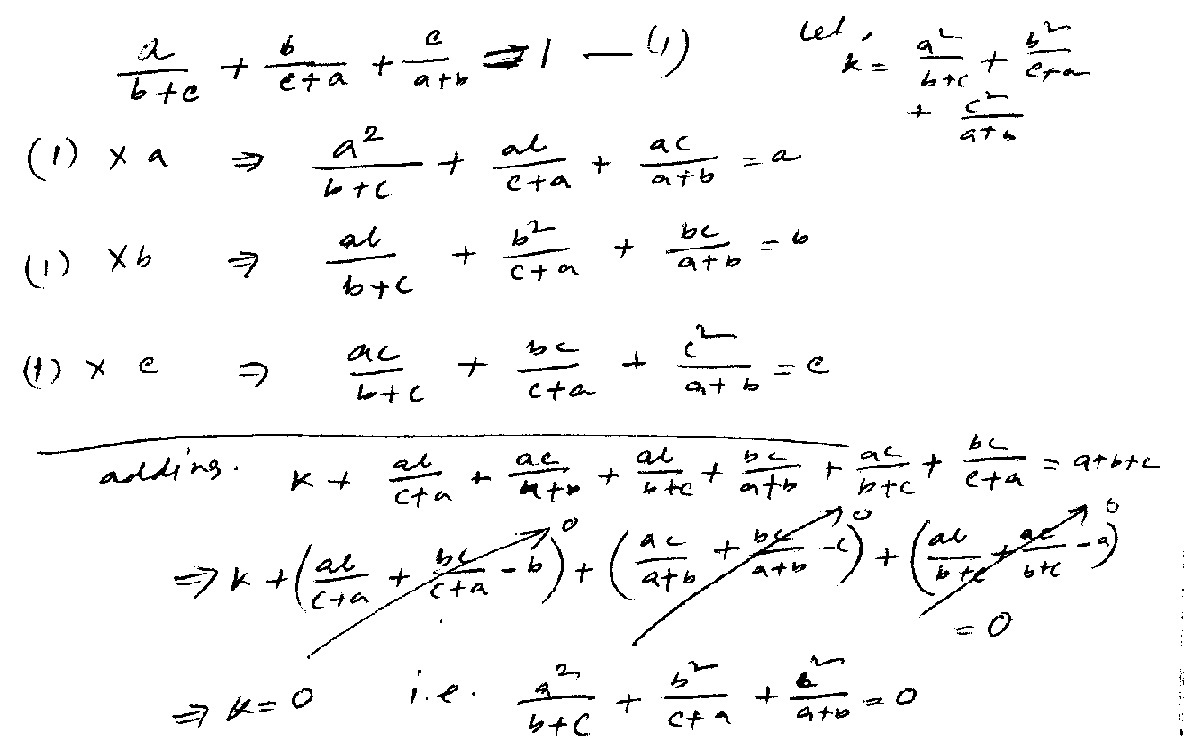
We rewrite the expression into
b + c a + a + c b + a + b c = a + b + c a + b + c .
Multiplying both sides by a + b + c , we get
b + c a 2 + a + a + c b 2 + b + a + b c 2 + c = a + b + c .
Subtracting a + b + c from both sides,
b + c a 2 + a + c b 2 + a + b c 2 = 0 .
Edit: Oops! I didn't mean to copy the comment of Mr. Sahil. My computer was just so slow that I couldn't see the comment that time. So I thought there was no "proper" solution for this. And instead placed mine. Hope this resolves any misconceptions (I guess).