Basic Kinematics?
A particle is initially at rest and at the origin. The particle starts to move such that its acceleration a , displacement x at time t are related as a ∝ t x , where the proportionality constant is unity with suitable SI units.
Find the speed of the particle at t = 1 second.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The given equation is an Emden–Fowler Equation y ′ ′ = A x n y m .
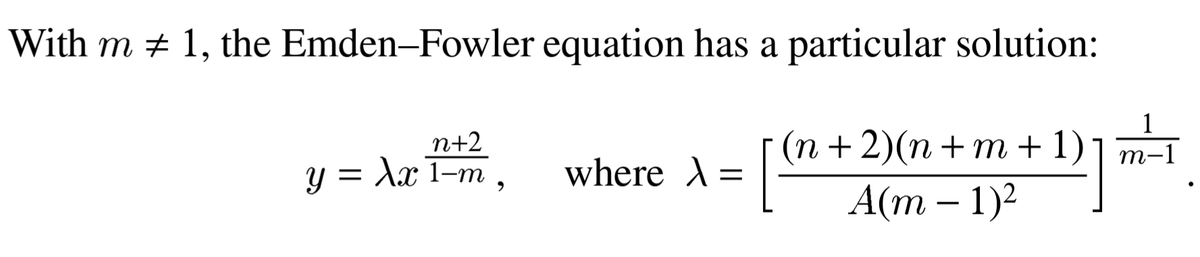
More information can be found here : in the book titled Handbook of Exact Solutions for Ordinary Differential Equations
Log in to reply
From a brief read of a paper on the FE equation, this is a particular solution, but I have yet to find a discussion about other solutions, so it is still not clear why your given solution is the only solution to the problem!
Log in to reply
With the given two initial conditions: y ( 0 ) = 0 and y ′ ( 0 ) = 0 , i believe there can only be one particular solution to a second order DE.
Log in to reply
@Digvijay Singh – No, because, as already observed, y ( x ) ≡ 0 also satisfies the equation with those boundary conditions!
Under certain conditions, ODEs have a unique solution, at least locally. The square root in this equation means, I think, that the normal conditions for a unique solution are not satisfied, if (as you are) you are working with initial conditions at t = 0 . Indeed, they cannot be satisfied, since there are at least two solutions to the equation.
Log in to reply
@Mark Hennings – I numerically integrated the equation - it seems that x ( t ) = c t 6 and x ( t ) = 0 are the only possible solutions. The latter is trivial, and the former required an arbitrarily small initial perturbation, such as x ( 0 ) = 0 . 0 0 0 1 .
As I am new to this concept, Can you please tell me why did you chose minimal one, I mean how can I be sure that this is the only solution? But anyway nice solution
Looking for a solution of the form x = A t α , we require that α ( α − 1 ) A t α − 2 = A t 2 1 α + 1 t ≥ 0 so we need α ( α − 1 ) A = 1 and α − 2 = 2 1 α + 1 . Thus α = 6 and A = 9 0 0 1 , so that x = 9 0 0 1 t 6 and the speed v = 1 5 0 1 t 5 . At time t = 1 , the speed is 1 5 0 1 m/s.
However, another perfectly good solution of the problem is x ≡ 0 , so it is not entirely clear why the first solution is guaranteed!
Why are we looking for a solution of the form x = A t α ?
Log in to reply
@Steven Chase @Mark Hennings Sir, please explain why to look for a solution of this type only???? How do we know that solutions are of these form....???
The particle needs an infinitesimal "nudge" to get out of the gate at all, otherwise it will be stuck at x = 0 for all t , as you have noted. I'm just curious how we would go about introducing this "nudge" as an initial condition; would we have to state that x ′ ( 0 ) = δ > 0 and then let δ → 0 to get the final solution and to correspond to the form of solution you have suggested?
Log in to reply
It is stated in the question that ' the particle starts to move '. So that rules out the possibility of x = 0
This bothered me too.
We have the differential equation x ¨ ( t ) = t x ( t ) . This is both nonlinear and second-order, so it looks like solving it would be a lost cause. However, we can try homogenizing this equation (this won't usually work for differential equations with more than two terms). This essentially means assuming the x ( t ) is a polynomial and requiring the degree of both sides to be equal. Say that x ( t ) is given by a polynomial of some degree, n , in t . Since differentiating twice lowers the degree by 2 , we have: n − 2 = n / 2 + 1 Solving gives us n = 6 . Taking a minimal polynomial x ( t ) = c t 6 and plugging it into the differential equation yields: 3 0 c t 4 = c t 4 c = 3 0 1 c = 9 0 0 1 So we now know that x ( t ) = 9 0 0 1 t 6 is a solution to this differential equation. Finding its velocity leads to x ˙ ( t ) = 9 0 0 6 t 5 = 1 5 0 1 t 5 FInally, x ˙ ( 1 ) = 1 5 0 1