Basketball player

Classical Mechanics Level 2

'Not an original problem'. i felt that this is nice.so, i wanted to share it.

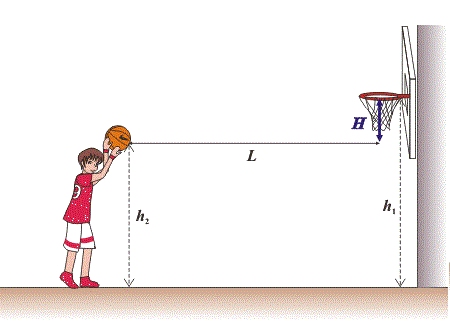
A basketball hoop is placed at a height $h_1$ above the floor. The centre of the basket is at a distance $L$ horizontally from the free-throw line. A basketball player shoots free throws and the ball leaves his hand in a moment where its centre is exactly above the free-throw line at a height $h_2$ above the floor.

The optimal elevation angle $\alpha$ is an angle in which the centre of the ball passes through the hoop centre, while the minimal initial ball velocity is needed. Prove generally, that this angle is $\alpha = 45^\circ + \beta/2$ , where $\beta$ is the tangent angle, i.e. the deviation of a line connecting the hoop centre and the starting point of the shot from the horizontal plane.

Calculate the corresponding initial velocity of the ball (in $\text{m/s}^2$ ).

Details and Assumptions:

Air resistance is negligible.
$h_1 = \text{3.05 m}$ , $L = \text{5.425 m}$ , $h_2 = \text{2.45 m}$ , $g = \text{9.81 m/s}^2$

3.3 6.6 2.2 5.5 14.98 10.1 7.7 4.4

1 solution

Chew-Seong Cheong
Feb 27, 2019

Consider the trajectory of the ball $h_2$ above ground. Let the initial velocity be $v$ , elevation angle be $\theta$ , and $h_1-h_2 = h$ . Then the $x$ and $y$ displacements time $t$ after shooting are given by $x = vt \cos \theta$ and $y = vt\sin \theta - \dfrac 12 gt^2$ . Substituting $t = \dfrac x{v\cos \theta}$ , we have $y = x\tan \theta - \dfrac {gx^2}{2v^2} \sec^2 \theta$ and the range $D = \dfrac {2v}g \sin 2\theta$ .

For the ball passing through the centre of the basket, then the trajectory passes through the point $(L, h)$ and

$\begin{aligned} h & = L\tan \alpha - \frac {gL^2}{2v^2} \sec^2 \alpha & \small \color{#3D99F6} \text{Since } \tan \beta = \frac hL \\ \tan \beta & = \tan \alpha - \frac {gL}{2v^2} \sec^2 \alpha & \small \color{#3D99F6} \text{Rearranging} \\ \color{#3D99F6} v \sqrt{\frac 2{gL}} & = \color{#3D99F6} \frac {\sec \alpha}{\sqrt{\tan \alpha-\tan \beta}} \quad ...(1) & \small \color{#3D99F6} \frac d{d\alpha}\text{ both sides} \\ \sqrt{\frac 2{gL}} \frac {dv}{d\alpha} & = \frac {2\sec \alpha \tan \alpha (\tan \alpha-\tan \beta)- \sec^3 \alpha}{2(\tan \alpha-\tan \beta)^\frac 32} \end{aligned}$

When $v$ is minimum, $\dfrac {dv}{d\alpha}=0$ , then we have

$\begin{aligned} 2\tan\alpha (\tan\alpha - \tan \beta) & = \sec^2 \alpha = 1+\tan^2 \alpha \\ \tan^2 \alpha - 2 \tan \beta \tan \alpha - 1 & = 0 \end{aligned}$

$\begin{aligned} \implies \tan \alpha & = \tan \beta + \sqrt{\tan^2 \beta + 1} = \tan \beta + \sec \beta & \small \color{#3D99F6} \text{By half-angle tangent substitution} \\ & = \frac {2\tan \frac \beta 2}{1-\tan^2 \frac \beta 2} + \frac {1+\tan^2 \frac \beta 2}{1-\tan^2 \frac \beta 2} \\ & = \frac {\left(1+\tan \frac \beta 2\right)^2}{\left(1+\tan \frac \beta 2\right)\left(1-\tan \frac \beta 2\right)} \\ & = \frac {1+\tan \frac \beta 2}{1-\tan \frac \beta 2} = \tan \left(45^\circ + \frac \beta 2\right) \\ \implies \alpha & = 45^\circ + \frac \beta 2 \end{aligned}$

From $\color{#3D99F6} (1): \ v \sqrt{\dfrac 2{gL}} = \dfrac {\sec \alpha}{\sqrt{\tan \alpha-\tan \beta}}$ $\implies v \approx \boxed{7.7}$ .

@chakravarthy b , since you are not the originator of the problem, you should give credit to the originator or mention "Not an original problem". You can enter h _ 1 $h_1$ , v _ 1^2 $v_1^2$ , \alpha = 45^\circ + \beta/2 $\alpha = 45^\circ + \beta/2$ , g = \text{9.81 m/s}^2 $g = \text{9.81 m/s}^2$ .

Chew-Seong Cheong - 2 years, 3 months ago

@Chew-Seong Cheong you are correct. i felt that this is nice.so, i wanted to share it.

chakravarthy b - 2 years, 3 months ago

You must mention where is the source of the problem. Otherwise, you are claiming it is your own.

Chew-Seong Cheong - 2 years, 3 months ago

@Chew-Seong Cheong – @Chew-Seong Cheong ok.

chakravarthy b - 2 years, 3 months ago

Basketball player

1 solution

0 pending reports