Batman's Two-Face-Four-Face Probability

Probability Level 4

Suppose we start with one fair die with no labels, and we label each of the $6$ faces with a distinct integer between $1$ and $6$ . When the die is rolled, $4$ numbers that are facing neither up nor down altogether yield the sum. For example, if the rolled die has the faces labeled as shown below, then the sum is $1 + 2 + 3 + 6 = 12$ . Other possible sums are $14$ (from $2 + 3 + 4 + 5$ ) and $16$ (from $1 + 4 + 5 + 6$ ).

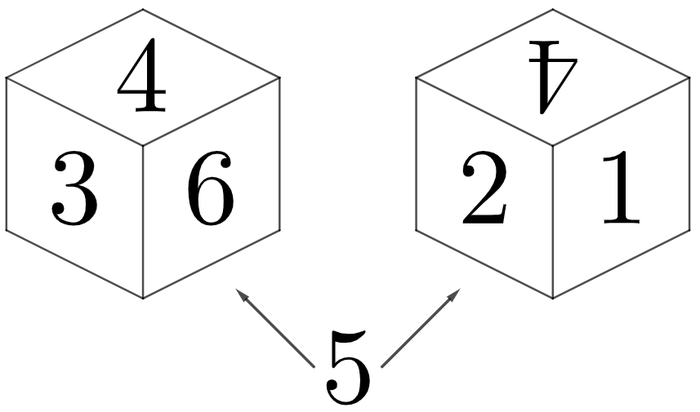$Both diagrams illustrate two distinct views on a labeled die after it was rolled. The left shows three labeled faces of a die. If we rotate it $180^{\circ}$ as shown on the right, the other two shown faces are $2$ and $1$. Since $4$ is facing up and $5$ is facing down, those numbers are not counted toward the sum.$ Both diagrams illustrate two distinct views on a labeled die after it was rolled. The left shows three labeled faces of a die. If we rotate it $180^{\circ}$ as shown on the right, the other two shown faces are $2$ and $1$ . Since $4$ is facing up and $5$ is facing down, those numbers are not counted toward the sum.

What is the probability of labeling the die, such that it has at most two distinct possible sums of $4$ numbers?

\dfrac{1}{3}

\dfrac{1}{4}

\dfrac{1}{5}

\dfrac{1}{6}

\dfrac{1}{9}

None of the given choices.

1 solution

Saya Suka
Mar 9, 2021

There are 5 ways to get at most 2 distinct sums. The total sum on a die is 1+2+3+4+5+6 = 21. If the wall-sums are m, m and n (wall-sum : the total when the numbers on the four vertical faces on a die are added together), then these would be complemented by 21-m, 21-m and 21-n as the updown-sums, for which x+x+y = 21 with x = 21-m and y = 21-n.

21 = y + x + x
= 3 + 9 + 9
= 5 + 8 + 8
= 7 + 7 + 7
= 9 + 6 + 6
= 11 + 5 + 5
since the smallest updown-sum is 1+2 = 3 and the biggest updown-sum is 6+5 = 11.

Total distinct triple pairings
= 6! / [(2!2!2!) x 3!]
= 15

P(labeling with at most 2 distinct sums)
= 5 / 15
= 1 / 3

Shouldn’t x+x+y be equal to 42(doesn’t affect the solution)

Jason Gomez - 3 months ago

No, as he chose $x$ and $y$ to be related to the "updown-sums". In general, the sum of these three sums is $21$ . The sum of the three wall sums is $42$ .

Michael Huang - 3 months ago

Then I think I haven’t understood the first part of the solution well, isn’t m+m+n=21 cause they are the sum of opposite faces of the die?

Jason Gomez - 3 months ago

Oh got it now never mind the above comment

Jason Gomez - 3 months ago

@Saya Suka : I could not understand how you calculated the total distinct triple pairings. May you please explain again?

Paul Romero - 3 months ago

6! is the distinctive ways to label the 6 numbers, but a cube has 3 pairs of opposite faces, thus the division with (2!)³ for non-distinction between floor vs ceiling (no fixed North pole nor South pole, that is, 1 + 2 = 2 + 1). 3! is for the non-distinguishability of the opposite pairs (rotation of the cube on its own √3 diagonal as axis will show that any 2 opposing faces can be of floor-ceiling pair or front-back wall pair or right-left wall pair).

Saya Suka - 3 months ago

@Saya Suka : I did it manually, and I only could find 13: (3, 7, 11), (3, 8, 19), (3, 9, 9), (4, 6, 11), (4, 7, 10), (4, 8, 9), (5, 5, 11), (5, 6, 10), (5, 7, 9), (5, 8, 8), (6, 6, 9), (6, 7, 8) and (7, 7, 7). Please, help me to find the other 2.

Paul Romero - 3 months ago

@Paul Romero – (5, 7, 9) and (6, 7, 8) has two distinct dice each.

1) [ 1+4 / 2+5 / 3+6 ] vs [ 2+3 / 1+6 / 4+5 ] , and
2) [ 2+4 / 1+6 / 3+5 ] vs [ 1+5 / 3+4 / 2+6 ]

Saya Suka - 3 months ago

@Saya Suka – Sorry for annoying you, but I do not understand it . May you explain it, please?

Paul Romero - 3 months ago

@Paul Romero – 5 = 1+4 = 2+3
7 = 2+5 = 1+6
9 = 3+6 = 4+5

You have 2 visually different dice but their opposition sums are the same.

Saya Suka - 3 months ago

@Saya Suka – Wow!!!!! You are right!!!!! Thank you so much!!!!

Paul Romero - 3 months ago

@Saya Suka – I will study the whole problem now to finally understand the whole process. Thank you so much!!!

Paul Romero - 3 months ago

@Paul Romero –

Die	A	B
Ceiling	1	3
Floor	4	2
North wall	5	6
South wall	2	1
East wall	6	4
West wall	3	5

The positions can be rotated to whatever, but must be done to both dice. Also, 1+4 = 4+1 = 3+2 = 2+3

Saya Suka - 3 months ago

This is beautiful, noting that there are always 2 distinctive ways of labeling the die in each of these 5 cases, but any die has always triple pairing and also two distinctive ways of labeling the die to make each triple pairing, and 10/30 is same 5/15 = 1/3

A Former Brilliant Member - 2 months, 3 weeks ago

Batman's Two-Face-Four-Face Probability

1 solution

0 pending reports