Battle between Rod and Cube

A massless Rod of Length 'L' with small Stone of mass ' m ' at the end is Hinged at point 'O' as shown in the figure and occupies a strictly Vertical Position, touching a body of mass M . A Light Gentle jerk sets the system in motion. For what mass ratio M/m will the rod form an angle α with the horizontal at the moment of the separation from the body ? Friction should be neglected everywhere. if it can be expressed as m M = sin c α a − b sin α
Then Find a + b + c
Assumptions
∙ Here assume That α ∈ ( o , 2 π )
Source : Asked in my test
Try more Deepanshu's Mechanics Blast's
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is Interesting Question Deepanshu Bro ! ⌣ ¨ . I enjoyed in solving this.
Its from krotov seen it previously
Log in to reply
May Be Possible , Actually It was asked in our Recent Review Test ,in our Coaching Institute, I liked it , So I shared it .
And Btw what is ' Krotov ' is it a Book ?
Log in to reply
Ya SS Krotov by MIR Publishers. Its a fantastic collection of problems. Its one level above irodov
Log in to reply
@Rohit Shah – Ohh :O , I really doesn't Know about it . But, Is there any online pdf for this Book ? or any ebook Link That You Know ? Thanks!
Log in to reply
@Deepanshu Gupta – search it online, its so popular you will find a thousand correct links for it, its like iridov except harder as per me
Log in to reply
@Mvs Saketh – Thanks ! But when I Searched Then I didn't Getting appropriate Link for it . Can you please Provide Valid Link of it for me ? Thanks Saketh
@Rohit Shah – Hey!please don't underestimate Krotov.It's 10 levels above Irodov
Why are we neglecting Tension in the rod ?
Log in to reply
Where are we neglecting it?Or rather why should it be included?
It neither does any work , nor do it provides any torque.
Log in to reply
You are neglecting tension when you consider centripetal acceleration.Yes it doesnt do any work, but it cannot be neglected when you write your force equations
Log in to reply
@Sumanth R Hegde – But we are not considering centripetal acceleration, coz finding tension is difficult in this scenario, thus we are not writing that equation.
Log in to reply
@Harsh Shrivastava – . m g s i n ( α ) + T+ N c o s ( α ) = m w 2 l ......This should have been the equation ....Get my point??
Log in to reply
@Sumanth R Hegde – You are right I guess, I didn't read his solution carefully.
What I did was to use the tangential motion equation for the stone :
m g l c o s x − N l s i n x = I s a t
I think u missed out the tension term in your second equation
The actual equations should be written as
For a general angle x :
Ncos(x) + mgsin(x) - T = mv²/l . . . ( 1 )
N = Ma . . . ( 2 )
T cosx - N = ma . . . ( 3 )
Simultaneously solving 1, 2 and 3 we get:
Ncosx - Nsecx(M+m)/(m)+ mgsinx = mv²/l
At the moment of break off these equations still hold as N(normal force) still exists, it is just that it has become infinitesimally small and hence N can be neglected from the final equation
Let V be the velocity of the Cube and v be the velocity of the upper end of the rod at the moment they get separated.
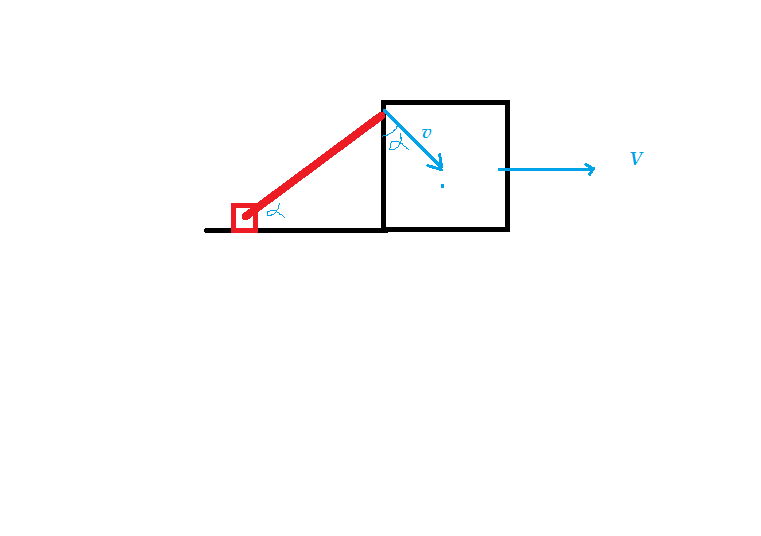
So by conservation of energy
m g l ( 1 − s i n α ) = 2 1 ( M V 2 + m v 2 )
As they just loose contact so till then the velocities of points in contact , perpendicular to the contact surface must be equal
so v s i n α = V
Substituting this in our 1st equation we get
V 2 = ( m + M s i n 2 α ) 2 m g l s i n 2 α ( 1 − s i n α )
After the moment m loose contact with the M no force acts on it so
d t d v = 0 or d α d v d t d α = 0
Now as d α d V = 0
So d α d V 2 = 0
So d α d { ( m + M s i n 2 α ) 2 m g l s i n 2 α ( 1 − s i n α ) } = 0
On solving this we get
m M = s i n 3 ( α ) 2 − 3 s i n ( α )
Nicely Done !
Log in to reply
@satvik pandey - Nice method , but it would have been much simple if you differentiated that vsina = V equation itself to find a relation between w and alpha and then use the fact that torque is only provided by gravity at the instant seperation and hence find alpha (angular acceleration), from there find w, and then use energy conservation
Log in to reply
The differentiation was quite long. Could please upload your whole solution. :)
Log in to reply
@Satvik Pandey – w l s i n ( θ ) = v u s i n g d θ / d t = − w d w / d t = α w e g e t α t a n ( θ ) = w 2 s i n c e o n l y g r a v i t y p r o v i d e s t o r q u e α = l g c o s ( θ ) w 2 = l g s i n ( θ ) s o m g l = m g l s i n ( θ ) + 2 m l 2 w 2 + 2 M v 2 sorry for inputting all in latex, i had to save time
Note that i used dv/dt = 0 to derive the first relation
then 1 = 2 3 s i n ( θ ) + m M 2 ( s i n ( θ ) ) 3
Log in to reply
@Mvs Saketh – Thank you Saketh for explaining. Your method is ingenious. :)
@Mvs Saketh – then u know what to do
Thanks bro! :)
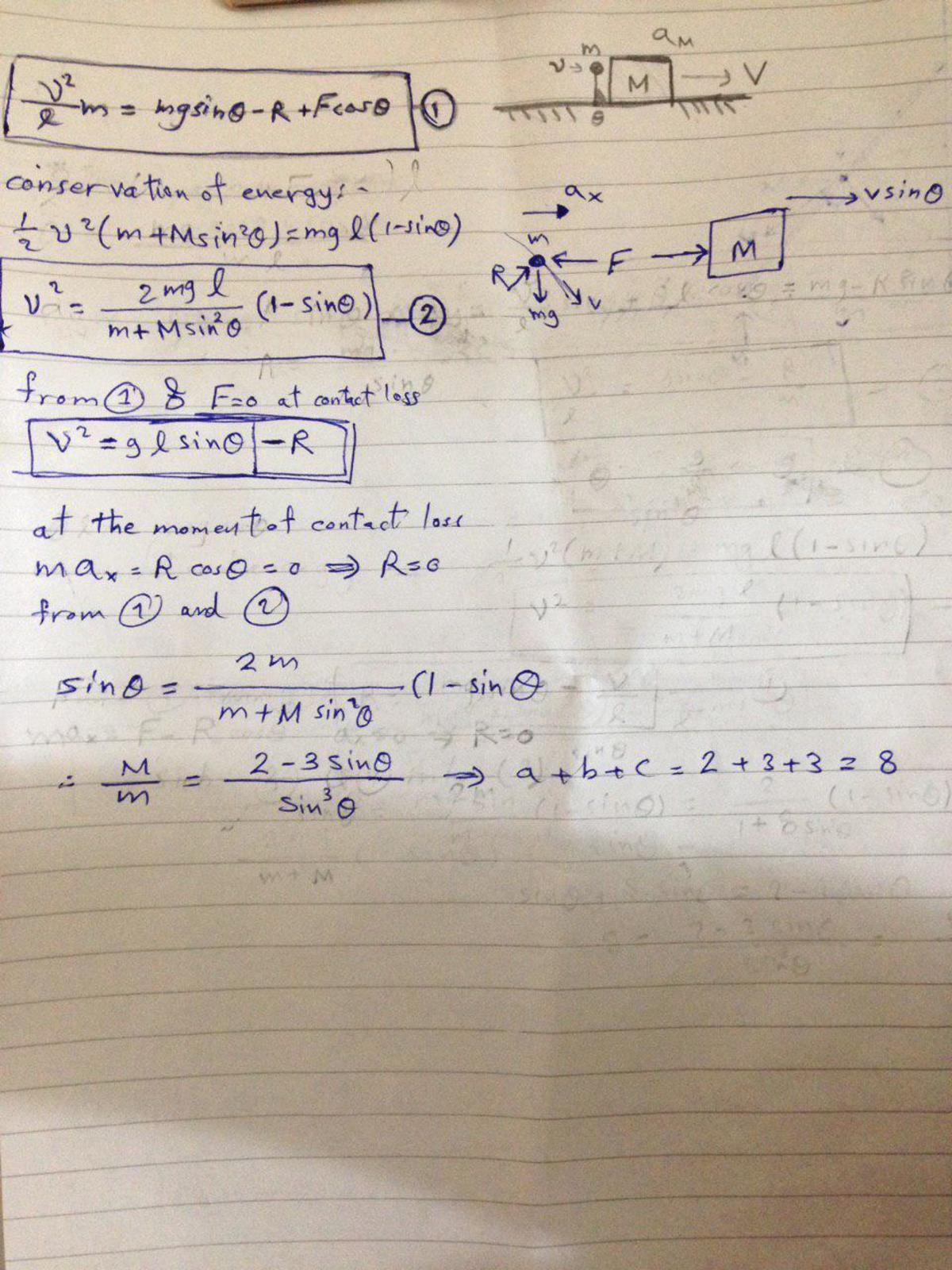
At the instant of separation, Let Cube has Velocity 'V' and rod has angular velocity ω about the point 'O' . Then Using Energy Conservation (System Rod + Cube+Earth)
m g L ( 1 − sin α ) = 2 1 ( m L 2 ) ω 2 + 2 1 m v 2 . . . ( 1 ) .
using angular equation of motion of Rod ; N cos α + m g sin α = m ω 2 L . . . ( 2 ) .
Condition of Sepration (Normal reaction must be zero) N = 0 . . . ( 3 ) .
Using Constrained Equation : (Relative Velocities of Point of Contact b/w rigid Bodies along Common Normal Must be zero , Because they are Rigid So their Inter Particle Distance Must not be Changed )
v = ω L sin α . . . ( 4 ) .
You Have 4 equations and 4 variable , Eliminate Them . and we should get ;
m M = sin 3 α 2 − 3 sin α .