Be careful with your licence plates!

In Kansas, vehicle licence plates each have exactly three letters followed by three digits. We are told that to produce such a licence plate, it costs $ n for each digit n > 0 and $ 1 0 for each digit 0 . For letters, the cost is proportional to the position of the letter in the alphabet, namely, $ 1 for A , $ 2 for B and so on, up to $ 2 6 for Z .
Determine how many different licence plates would cost exactly $ 1 0 0 .
The answer is 1287.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Could you explain why it is the same?
Log in to reply
The indistinguishable "balls" in this case are decrementations of each character by 1. (8 decrementations means that the license plate is guaranteed to be $100) There is allowed to be any number of them in a character (putting all of them in a digit is only 2, all in a letter is R), there are six characters, and the order matters. So, 8 identical balls in 6 different boxes.
It is truely brilliant ####
L
e
t
t
e
r
s
p
a
r
t
M
a
x
i
m
u
m
c
o
s
t
i
s
3
∗
Z
=
3
∗
2
6
=
7
8
,
⟹
d
i
g
i
t
p
a
r
t
M
i
n
i
m
u
m
c
o
s
t
i
s
2
2
.
D
i
g
i
t
p
a
r
t
M
a
x
i
m
u
m
c
o
s
t
i
s
3
∗
0
=
3
∗
1
0
=
3
0
,
⟹
l
e
t
t
e
r
p
a
r
t
M
i
n
i
m
u
m
c
o
s
t
i
s
7
0
.
S
o
w
e
s
h
a
l
l
h
a
v
e
9
g
r
o
u
p
s
o
f
p
l
a
t
e
s
.
P
l
a
t
e
s
(
D
i
g
i
t
p
a
r
t
c
o
s
t
+
L
e
t
t
e
r
p
a
r
t
c
o
s
t
=
1
0
0
)
=
(
2
2
+
7
8
)
/
(
2
3
+
7
7
)
/
(
2
4
+
7
6
)
(
2
5
+
7
5
)
/
(
2
6
+
7
4
)
/
(
2
7
+
7
3
)
(
2
8
+
7
2
)
/
(
2
9
+
7
1
)
/
(
3
0
+
7
0
)
S
a
m
e
n
u
m
b
e
r
o
f
p
l
a
t
e
s
c
a
n
b
e
p
u
r
c
h
a
s
e
d
w
h
e
r
e
d
i
g
i
t
a
l
p
a
r
t
c
o
s
t
D
,
o
r
p
l
a
t
e
s
w
h
e
r
e
l
e
t
t
e
r
p
a
r
t
c
o
s
t
7
0
+
(
D
−
2
2
)
=
D
+
4
8
.
H
e
n
c
e
w
e
s
h
a
l
l
f
i
n
d
o
n
l
y
p
l
a
t
e
s
r
e
q
u
i
r
e
d
,
w
i
t
h
r
e
f
e
r
e
n
c
e
c
o
s
t
o
f
d
i
g
i
t
a
l
p
a
r
t
.
T
h
e
g
i
v
e
n
t
a
b
l
e
g
i
v
e
s
u
s
n
u
m
b
e
r
o
f
u
n
i
q
u
e
p
l
a
t
e
s
w
e
r
e
d
i
g
i
t
a
l
p
a
r
t
s
c
a
n
p
u
r
c
h
a
s
e
d
f
o
r
2
2
t
o
3
0
c
o
s
t
.
A
l
l
T
H
R
E
E
d
i
g
i
t
s
s
a
m
e
.
I
f
a
l
l
t
h
r
e
e
d
i
g
i
t
s
a
r
e
s
a
m
e
,
t
h
e
r
e
i
s
o
n
l
y
3
!
3
!
=
1
p
l
a
t
e
f
o
r
g
i
v
e
n
c
o
s
t
.
8
+
8
+
8
c
o
s
t
2
4
:
−
1
p
l
a
t
e
.
9
+
9
+
9
c
o
s
t
2
7
:
−
1
p
l
a
t
e
.
1
0
+
1
0
+
1
0
c
o
s
t
3
0
:
−
1
p
l
a
t
e
.
T
W
O
d
i
g
i
t
s
s
a
m
e
.
I
f
t
w
o
d
i
g
i
t
s
a
r
e
s
a
m
e
w
e
c
a
n
h
a
v
e
2
!
3
!
=
3
p
l
a
t
e
s
w
i
t
h
d
i
f
f
e
r
e
n
t
a
r
r
a
n
g
e
m
e
n
t
f
o
r
g
i
v
e
n
c
o
s
t
.
F
o
r
d
i
f
f
e
r
e
n
t
c
o
s
t
,
t
h
e
t
a
b
l
e
b
e
l
o
w
g
i
v
e
s
n
u
m
b
e
r
o
f
p
l
a
t
e
s
w
h
e
r
e
t
w
o
d
i
g
i
t
s
a
r
e
t
h
e
s
a
m
e
.
C
o
s
t
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
1
0
+
1
0
+
?
1
0
+
1
0
+
2
1
0
+
1
0
+
3
1
0
+
1
0
+
4
1
0
+
1
0
+
5
1
0
+
1
0
+
6
1
0
+
1
0
+
7
1
0
+
1
0
+
8
1
0
+
1
0
+
9
P
l
a
t
e
s
3
3
3
3
3
3
3
3
9
+
9
+
?
9
+
9
+
4
9
+
9
+
5
9
+
9
+
6
9
+
9
+
7
9
+
9
+
8
9
+
9
+
1
0
P
l
a
t
e
s
.
3
3
3
3
3
3
8
+
8
+
?
8
+
8
+
6
8
+
8
+
7
8
+
8
+
9
8
+
8
+
7
1
0
P
l
a
t
e
s
3
3
3
3
7
+
7
+
?
7
+
7
+
8
7
+
7
+
9
7
+
7
+
1
0
P
l
a
t
e
s
3
3
3
6
+
6
+
?
6
+
6
+
1
0
P
l
a
t
e
s
3
T
o
t
a
l
P
l
a
t
e
s
1
5
1
2
9
9
9
3
6
3
A
l
l
T
H
R
E
E
d
i
s
t
n
i
c
t
d
i
g
i
t
s
.
I
f
a
l
l
t
h
r
e
e
d
i
g
i
t
s
a
r
e
d
i
s
t
i
n
c
t
w
e
c
a
n
h
a
v
e
3
!
=
6
p
l
a
t
e
s
w
i
t
h
d
i
f
f
e
r
e
n
t
a
r
r
a
n
g
e
m
e
n
t
f
o
r
g
i
v
e
n
c
o
s
t
.
S
i
n
c
e
c
o
s
t
o
f
2
8
,
2
9
,
3
0
d
o
n
o
t
h
a
v
e
a
n
y
p
l
a
t
e
w
i
t
h
t
h
r
e
e
d
i
s
t
i
n
c
t
d
i
g
i
t
s
,
t
h
e
y
a
r
e
n
o
t
i
n
t
h
e
t
a
b
l
e
b
e
l
l
o
w
.
W
h
e
n
a
l
l
d
i
g
i
t
s
a
r
e
d
i
f
f
e
r
e
n
t
,
t
o
g
e
t
t
h
e
p
l
a
t
e
c
o
s
t
o
f
1
0
0
,
t
h
e
d
i
g
i
t
a
l
p
a
r
t
m
u
s
t
h
a
v
e
o
n
e
d
i
g
i
t
c
o
s
t
i
n
g
9
o
r
1
0
o
n
l
y
.
S
o
t
h
e
t
a
b
l
e
b
e
l
o
w
.
C
o
s
t
2
2
2
3
2
4
2
5
2
6
2
7
1
0
i
s
o
n
e
o
f
t
h
e
d
i
g
i
t
s
.
1
0
+
9
+
3
1
0
+
8
+
4
1
0
+
7
+
5
1
0
+
9
+
4
1
0
+
8
+
5
1
0
+
7
+
6
1
0
+
9
+
5
1
0
+
8
+
6
1
0
+
9
+
6
1
0
+
8
+
7
1
0
+
9
+
7
1
0
+
9
+
8
P
l
a
t
e
s
6
6
6
6
6
6
6
6
6
6
6
6
9
i
s
o
n
e
o
f
t
h
e
d
i
g
i
t
s
.
9
+
8
+
5
9
+
7
+
6
9
+
8
+
6
9
+
8
+
7
P
l
a
t
e
s
6
6
6
6
T
o
t
a
l
P
l
a
t
e
s
3
0
p
l
a
t
e
s
c
o
s
t
2
2
e
a
c
h
.
2
4
p
l
a
t
e
s
c
o
s
t
2
3
e
a
c
h
.
1
8
p
l
a
t
e
s
c
o
s
t
2
4
e
a
c
h
.
1
2
p
l
a
t
e
s
c
o
s
t
2
5
e
a
c
h
.
6
p
l
a
t
e
s
c
o
s
t
2
6
e
a
c
h
.
6
p
l
a
t
e
s
c
o
s
t
2
7
e
a
c
h
.
F
r
o
m
t
h
e
a
b
o
v
e
,
w
e
g
e
t
t
h
e
c
o
n
s
o
l
i
d
a
t
e
d
t
a
b
l
e
b
e
l
o
w
.
c
o
s
t
o
f
d
i
g
i
t
a
l
p
a
r
t
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
3
0
A
l
l
s
a
m
e
d
i
g
i
t
s
0
0
1
0
0
1
0
0
1
T
w
o
d
i
g
i
t
s
s
a
m
e
+
1
5
+
1
2
+
9
+
9
+
9
+
3
+
6
+
3
+
0
A
l
l
d
i
s
t
i
n
c
t
d
i
g
i
t
+
3
0
+
2
4
+
1
8
+
1
2
+
6
+
6
+
0
+
0
+
0
T
o
t
a
l
p
l
a
t
e
s
=
4
5
=
3
6
=
2
8
=
2
1
=
1
5
=
1
0
=
6
=
3
=
1
c
o
s
t
o
f
l
e
t
t
e
r
p
a
r
t
.
7
0
7
1
7
2
7
3
7
4
7
5
7
6
7
7
7
8
P
l
a
t
e
s
f
o
r
e
a
c
h
g
r
o
u
p
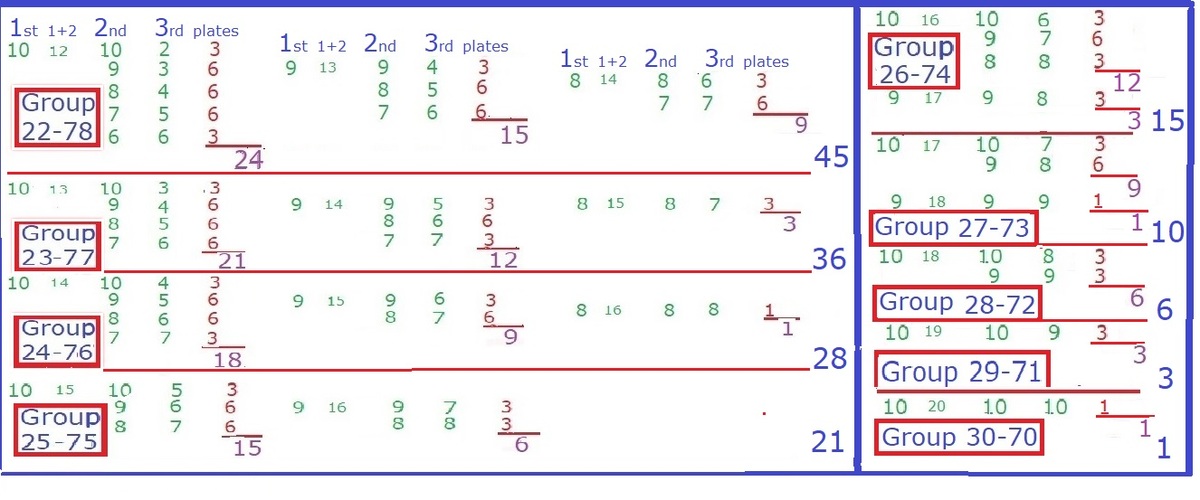
G
r
o
u
p
2
2
−
7
0
2
3
−
7
1
2
4
−
7
2
2
5
−
7
3
2
6
−
7
4
2
7
−
7
5
2
8
−
7
6
2
9
−
7
7
3
0
−
7
8
D
i
g
i
t
a
l
p
a
r
t
p
l
a
t
e
s
∗
L
e
t
t
e
r
p
a
r
t
p
l
a
t
e
s
4
5
∗
1
3
6
∗
3
2
8
∗
6
2
1
∗
1
0
1
5
∗
1
5
1
0
∗
2
1
6
∗
2
8
3
∗
3
6
1
∗
4
5
=
T
o
t
a
l
p
l
a
t
e
s
o
f
t
h
e
g
r
o
u
p
.
=
4
5
=
1
0
8
=
1
6
8
=
2
1
0
=
2
2
5
=
2
1
0
=
1
6
8
=
1
0
8
=
4
5
T
o
t
a
l
u
n
i
q
u
e
p
l
a
t
e
s
e
a
c
h
c
o
s
t
i
n
g
1
0
0
$
1
2
8
7
.
We can also use the tables below to find plates for Digit parts and then as above.
The answer is the coefficient of x 1 0 0 in the following polynomial: ( x + x 2 + . . . + x 1 0 ) 3 ( x + x 2 + . . . + x 2 6 ) 3 Which is by factorization the coefficient of x 9 4 in the following polynomial: ( 1 + x + . . . + x 9 ) 3 ( 1 + x + . . . + x 2 5 ) 3 Which is the coefficient of x 8 in the same polynomial since this polynomial is Palindromic : ( 1 + x + . . . + x 9 ) 3 ( 1 + x + . . . + x 2 5 ) 3 Which is by removing power more than 8 the coefficient of x 8 in the following polynomial: ( 1 + x + . . . + x 8 ) 6 ( 1 + x + . . . + x 8 ) 6 = ( 1 − x ) 6 ( 1 − x 9 ) 6 let's take a detour through analysis: ( 1 − x 9 ) 6 = 1 + O ( x 9 ) and by Taylor series: ( 1 − x ) 6 1 = 1 + 6 x + 2 1 x 2 + 5 6 x 3 + 1 2 6 x 4 + 2 5 2 x 5 + 4 6 2 x 6 + 7 9 2 x 7 + 1 2 8 7 x 8 + O ( x 9 ) so that : ( 1 + x + . . . + x 8 ) 6 = 1 + 6 x + 2 1 x 2 + 5 6 x 3 + 1 2 6 x 4 + 2 5 2 x 5 + 4 6 2 x 6 + 7 9 2 x 7 + 1 2 8 7 x 8 + O ( x 9 )
and the answer is 1 2 8 7
I got it till here. How did you calculate the coefficient of x 1 0 0 ?
Log in to reply
I've added some details.
Log in to reply
What I mean by symmetry is that the polynomial is Palindromic
P ( x ) = ∑ i = 0 n a i x i is a polynomial of degree n, then P is palindromic if a i = a n − i for i = 0 , 1 , . . . , n
We use the facts that:
-
the product of two Palindromic polynomials is Palindromic polynomial,
-
and power of a Palindromic polynomial is Palindromic polynomial.
1 + x + . . . + x 9 is Palindromic ⟹ ( 1 + x + . . . + x 9 ) 3 is Palindromic
1 + x + . . . + x 2 5 is Palindromic ⟹ ( 1 + x + . . . + x 2 5 ) 3 is Palindromic
And finally ( 1 + x + . . . + x 9 ) 3 ( 1 + x + . . . + x 2 5 ) 3 is Palindromic
Log in to reply
@Abdelhamid Saadi – That's alright. I got that. Thanks! Didn't think about symmetry then.
i still don't get it how can it be symmetry?
1 2 3 4 5 6 7 8 9 10 11 |
|
1 |
|
Well what's the answer then?
Log in to reply
its hard if you using GF or inclusion exclusion (i have tried). so, i just coding it with c++. the answer is 1287. still waiting for great solution '-'
@Muhammad Ihsan Nice work!
In the future, you can actually display your code directly by copying and pasting it into something like this:

For example:
1 2 3 4 5 6 7 |
|
This will allow others to read and copy your code more easily. :)

The highest possible value is $108, for ZZZ 000. Finding the number of license plates that cost $100 dollars is equivalent to finding how many ways 8 indistinguishable balls can be placed in 6 distinguishable boxes, without exclusion. This leads to a value of 1287.