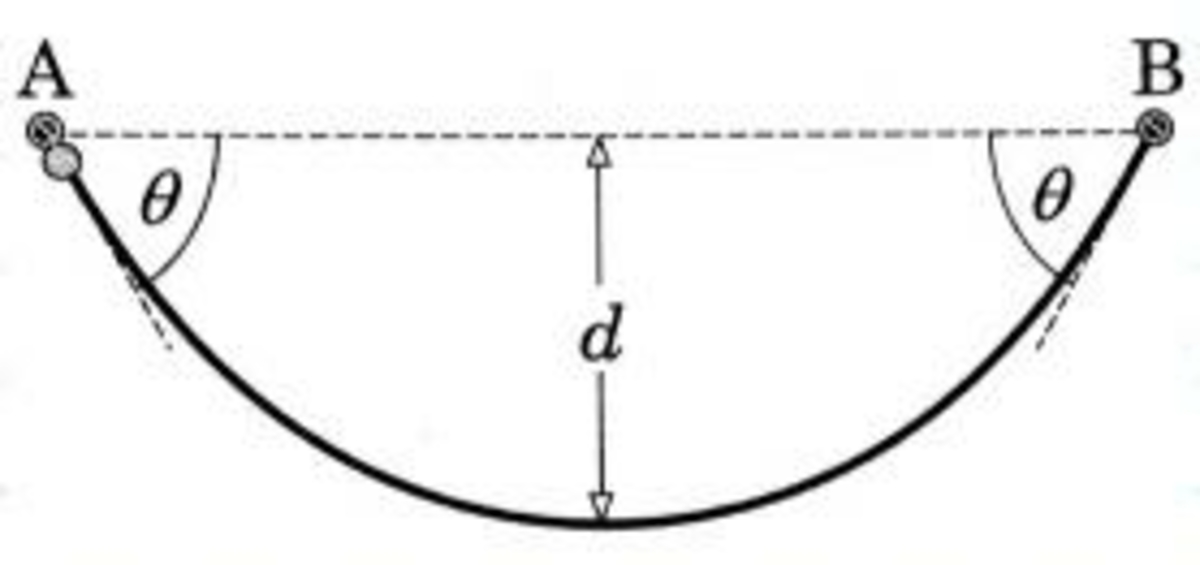
Bead and a Rope

This problem is a very good one.

Solving this requires some background knowledge. When a rope hangs between two points at the same level, the shape of the rope is a catenary. The equation of a catenary is:

$y = a \cosh{\frac{x}{a}}$

Where $a$ is constant. Let the lowermost point of the rope be the origin. The Y-axis points upwards while the X-axis points to the right. Let the coordinates of the points $A$ and $B$ be:

$A = (-x_o,d)$ $B = (x_o,d)$

Now, the length of the rope is $L$ which can be found using the following relation:

$L = \int_{-x_o}^{x_o} \sqrt{1 + \left(\frac{dy}{dx}\right)^2} \ dx$

Plugging in the derivative and solving the integral gives the result:

$L = 2a \sinh{\frac{x_o}{a}} \dots (1)$

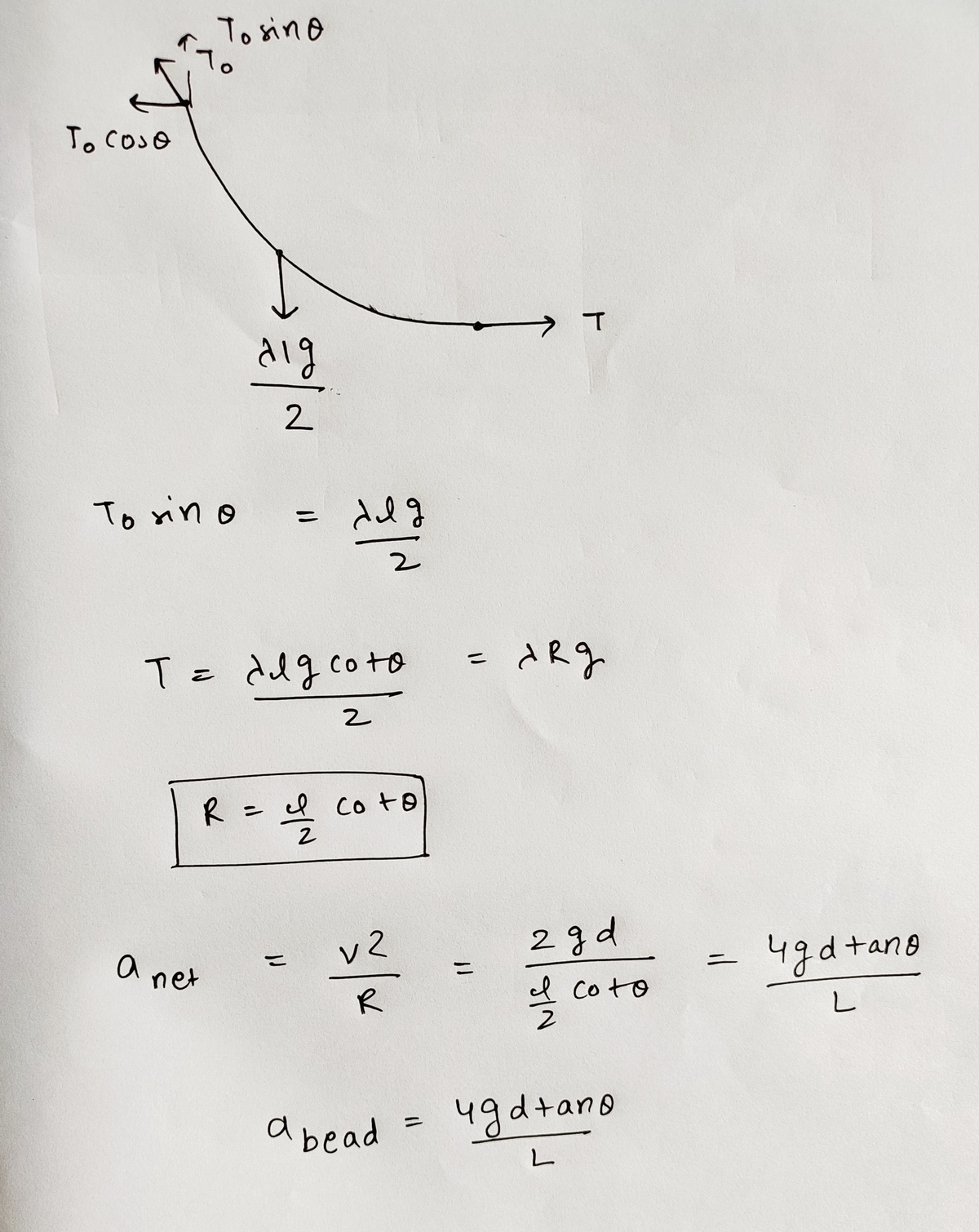
Now, the derivative at point $B$ is $\tan{\theta}$ . This gives the second equation as follows:

$\tan{\theta} = \sinh{\frac{x_o}{a}} \dots (2)$

From (1) and (2), we get:

$L = 2a \tan{\theta} \dots (3)$

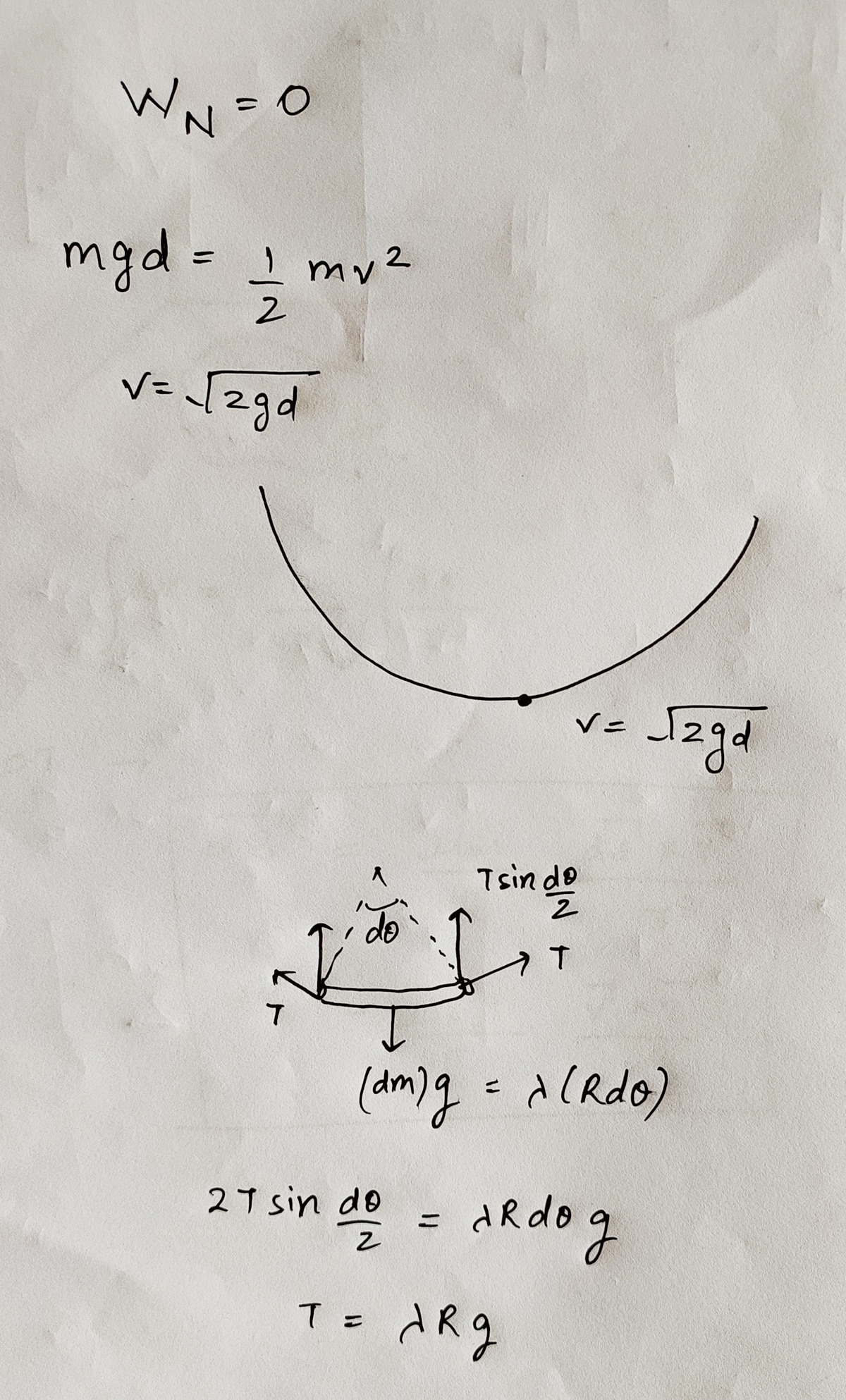
Now, consider the motion of the bead. By applying the energy conservation principle, the velocity acquired by the bead at the lowermost point is:

$v^2 = 2gd \dots(4)$

At the lowermost point, the bead moves horizontally. the net acceleration of the bead is it's centripetal acceleration which can be found as such:

$a_{bead} = \frac{v^2}{R}$ $a_{bead} = \frac{2gd}{R}$

Now, to find $R$ , the following formula can be applied at $x=0$ :

$R = \frac{\left(1 + \left(\frac{dy}{dx}\right)^2\right)^{3/2}}{\frac{d^2y}{dx^2}}$

Simplifying gives:

$R = a$

$\implies a_{bead} = \frac{2gd}{a}$

Using (3) and eliminating $a$ gives

$\implies a_{bead} = \frac{4gd\tan{\theta}}{L}$