Bead Sliding on Disk
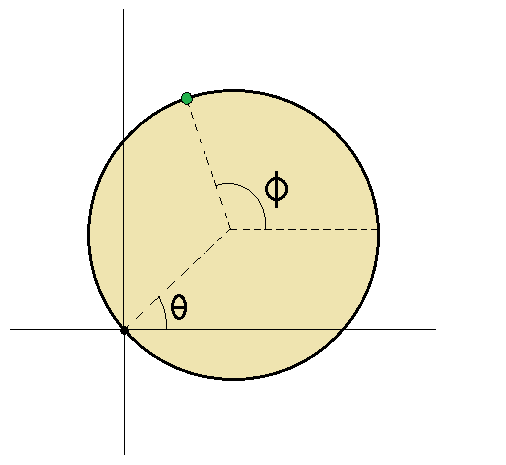
A uniform circular disk of mass M is confined to the x y plane. It rotates with no frictional losses about the z axis through a point on its edge. Gravity is into the page, and is thus irrelevant to this situation.
A bead of mass m slides along a friction-less track on the circumference of the disk. The angle θ is the angle between the positive x axis and a line from the origin to the center of the disk. The angle ϕ is the angle between the positive x axis and a line from the the center of the disk to the bead.
Let the " 0 " subscript denote the initial conditions.
θ 0 = 0 θ ˙ 0 = 0 ϕ 0 = 0 ϕ ˙ 0 = 0 M = 5 m
When ϕ − θ = 3 6 0 ∘ (indicating that the bead has gone once around the track), what is the value of θ (in degrees)?
Note:
This problem was inspired by a question from
Azimuddin Sheikh
Note:
The pivot point on the disk's edge does not interfere with the bead's motion
The answer is 63.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Indeed. It seems we would need two conservation laws instead of just one (maybe energy and momentum). I did it the Lagrange way as well
is angular momentum conserved
Log in to reply
Perhaps so. It may be possible to solve using conservation of kinetic energy and angular momentum.
Log in to reply
Since the Lagrangian L of the system, when expressed in terms of coordinates θ , ψ = ϕ − θ , is independent of θ , a first integral of Lagrange's equations is that ∂ θ ˙ ∂ L is constant. This statement is conservation of angular momentum. This statement, together with the fact that L is constant (conservation of energy) could be used to obtain solutions, but doing so would require making choices about signs of square roots, etc. It is probably easier to solve Lagrange's equations directly.
Log in to reply
@Mark Hennings – Well, OK, the moment of inertia of the disc about the point of rotation is 2 1 5 m R 2 = α m R 2 where α = 2 1 5 > 4 . The fact that α > 4 is enough to ensure that ψ ˙ is never zero, and hence we can always take the positive square root. If the intial value of ϕ ˙ is ω , then we obtain ψ ˙ θ ˙ = ω α + sin 2 ψ α − 2 + 2 cos ψ = α + 2 + 2 cos ψ ω [ 2 − ( 1 + cos ψ ) α + sin 2 ψ α − 2 + 2 cos ψ ] so that d ψ d θ = α + 2 + 2 cos ψ 1 ⎣ ⎡ 2 α − 2 + 2 cos ψ α + sin 2 ψ − 1 − cos ψ ⎦ ⎤ and hence the desired angle is ∫ 0 2 π α + 2 + 2 cos ψ 1 ⎣ ⎡ 2 α − 2 + 2 cos ψ α + sin 2 ψ − 1 − cos ψ ⎦ ⎤ d ψ which (reassuringly) evaluates to 6 3 . 2 ∘ .
Log in to reply
@Mark Hennings – That is a nice choice of generalised coordinates you've made. I instinctively chose the two angles only.
Thank you for the insights and for the helpful solution!
@Mark Hennings – I love Lagrange, because I don't have to worry about anything. I just write out the geometry and then mindlessly crunch out some derivatives.
Log in to reply
@Steven Chase – The power and simplicity of the Lagrangian approach is something I love as well. However, the physical interpretation involved in formulating equations of motion gets easily lost in such an approach. Working with constraints and reaction forces is a task completely eliminated (which is pretty neat as well)
Alternate approaches involving energy principles or anything else, are quite insightful.
about piovot
I posted the solution to a problem recently which again involved Lagrange's formulation. An alternate approach of solving the problem using the law of conservation of energy was suggested, which I really appreciated. I look forward to seeing a better approach to this problem. I tried to examine the expression of the energy of the system but it so happens that the generalised coordinates are coupled in a manner which makes manipulation of the energy equation harder, according to me.