Beam Balance Optimization

First you weigh gold and silver, lets say gold is heavier, then you take the bronze and weigh it against the gold. If bronze is heavier than gold then you have solved the order, and you only had to use the balance twice. But it is possible that the gold is heavier than both other coins and in that case you'll have to weigh the two other coins against each other to find which is lighter/heavier to solve for the order. It is possible to find the order in only 2 tries, however we are looking for the worst case scenario which will take 3 tries.

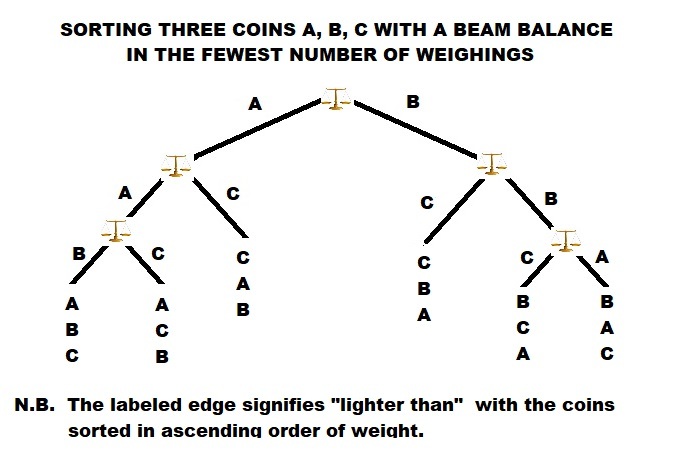
We'll call the three coins A, B, and C throughout this solution.

To make the measurement in three comparisons, we can measure A vs. B, B vs. C, and A vs. C. This means we know every coin's weight relative to the other two, so the three can easily be ordered.

Now we'd like to justify that the measurement can't be done in two weighings.

EASY METHOD:

Each weighing conveys a binary piece of information (either the scale goes to the left or to the right).

So each pair of weighings convey to us $2 \times 2 = 4$ pieces of information.

However, there are $3 \times 2 \times 1 = 6$ ways to order the three coins.

Since $4 < 6 ,$ in a worst case scenario there is not enough information to order the three coins.

LONGER METHOD:

This matches more closely the solution method some other people are attempting, and should indicate where any gaps might be.

We'll do this by looking at every measuring possibility and showing there is at least one possible outcome for each that makes the ordering impossible. Note we do have to account for the fact that an intelligent measurer can choose their second measurement based on the result of their first.

1st method: A single comparison followed by a single comparison

Suppose (without loss of generality) our first comparison is A vs B. We can assume A is heavier (both without loss of generality and also because we can create a worst-case scenario any way we desire).

So A > B. Now we can compare either A vs C or B vs C.

With A vs C, A > C indicates that while A is the heaviest coin, we don't know how to compare B and C.

With B vs C, B < C indicates that while B is the lightest coin, we don't know how to compare A and C.

2nd method: A single comparison followed by a dual comparison

Suppose (without loss of generality) our first comparison is A vs B. Again we can assume A is heavier.

So A > B. We can now compare A vs B+C, B vs A+C, or C vs A+B.

With A vs B+C, A > B+C conveys that A is the heaviest but nothing about B vs. C.

With B vs A+C, B < A+C conveys that B is the lightest but nothing about A vs. C.

With C vs A+B, C < A+B conveys nothing about A vs C or B vs C.

3rd method: Starting with a dual comparison

For a worst case scenario here, let's suppose the weights follow the triangle inequality:

Then any comparison of one coin vs. two will indicate the two coins are heavier! Therefore no information can be learned about their relative weights in this scenario.

This means that one follow-up measurement, whether single or dual, will not be able to determine a complete ordering.

For each coin, there are two others. So in the worst case scenario, there would be 3 x 2 possibilities, or 6, but you have to remember that you are counting each pairing twice, so it's 6/2, which is 3.

Considering the worst scenario you have this:

1 v 2

if we call the winner x, then we next have this:

x v 3

if x is less than three, we have a solution in two rounds. However, we have the worst, so x is less than 3, which then requires a third round of this:

3 vs the loser of the first round.

Two times. we can put one coin in the balance and record its weight, then the second one and record its weight. For the third one we can conclude based on its size where its weight lies before, after or between any of the previous records.

first wt. all the three of them .. then if we wt. any two of them we can get the wt. of the third ( by subtracting it from the previous observation) similarly we can get wt. of one more coin . and finally add the two and subtract it from the 1st observation to get the wt. of the last coin ... so total observations = 1+2=3

Since you have got three coins:bronze, silver and gold you will first start by weighing two at a time . For example you will first weigh that of bronze and gold, followed by silver and bronze then at last weigh gold and silver. When you get the masses of each pair ,you shall subtract to get the mass of each coin and at last you will weigh all the coins three times. SO THE ANSWER IS THREE TIMES.

Quick solution: There are $3!=6$ possible orderings of the coins, and we have to encode them by a string of 0/1s (say 0 for left scale being heavier and 1 for the right one), regardless of what we weigh against what. But one can encode only 4 outcomes by 2 weighings (00, 01, 10 and 11). And it's kind of easy to see that you can do it with 3.

I was alittle surprised that there was not a straight math solution, so here goes. Three unknowns require three equations to solve for each of the unknowns. In this case we cannot know the absolute values of the weights, but just the relative weights. weigh a vs b+c weigh b vs a+c weigh c vs a+b This will yield 3 equations such as a > b+c, b <c+c, c > a+b. The scale will tell you which way the inequality will go. > or <. Solve the three equations via substitution, addition and subtraction which will yield three inequalities such as b > a > c, for example

john neglia

Clearly there are three ways as you first have Weigh two and let one is heavier. Then replace lighter one with another,you find this on lighter to that of heavier one. Now put the heaviest one aside and compare lighter ones and you get the order of weight.

3!/(2!*1!)

For comparison sorting lower bound is floor n*log(n), where n denotes number of elements.

At first start with any two coin say gold and silver.

Weighting them on the balance we can found which one is more heavy.

Now taking heavier one with the bronze coin in the balance.

If we found bronze coin is heavier then we are done. But we have to consider the worst case so assume bronze coin is lighter than the heavy coin.

Then taking the bronze coin and the coin we found lighter at the first time.

Here we found the heavier one

So we are done.

Therefore minimum necessary steps is 3.

First, you weigh any two coins. Remember how low the heavier side got. Then, you take the lighter coin and weigh it against the last one.

If the coin that was originally lighter was heavier, then the order(from least to greatest) is Last One - Originally lighter - Originally Heavier.

If the coin that was originally lighter again was lighter, then compare how much the heavier side dropped in both cases. You should then get the answer.