Bend a bow strongly
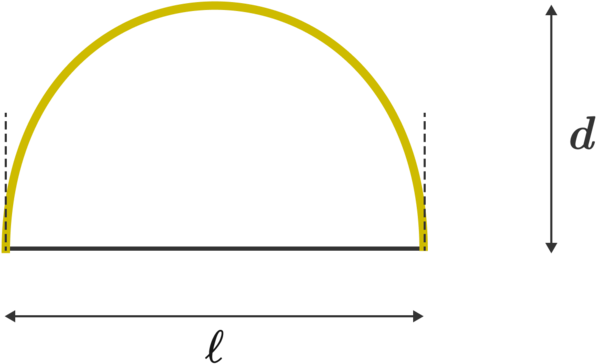
We tighten the black string of the bow until the bow's two ends are parallel, as indicated by the two dotted lines.
The distance between the string and the middle point of the bow is and the distance between the two ends is
What is the ratio
Assume that the bow is made of a material of uniform circular cross-section of radius with Before tightening the string, the bow was straight.
The answer is 0.8346.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
ρ 1 = ( 1 + y ′ 2 ) 3 / 2 y ′ ′ Eq.1
ρ 1 = d x d s d 2 y Eq. 2
The first equation is the standard formula from differential geometry. The second equation has an unusual "mixed" derivative, where d s is a line segment along the bow. We can derive it from Eq. 1 by using d s 2 = d x 2 + d y 2 .
If we use the first expression we get a second order nonlinear differential equation for the shape of the bow in the form of
( 1 + y ′ 2 ) 3 / 2 y ′ ′ = 2 c x ,
where 2 c is a constant that depends on the force, the elastic parameters and the cross section of the bow. The solution of this differential equation is by no means simple. The result is the so called "elastica" curve, first derived in a special case by James Bernoulli and in the most general case by Euler. Actually, the special case Bernoulli derived corresponds to the boundary conditions imposed in the problem here. Our solution is based on his ideas. (For a great historic perspective see this link ).
Instead of Eq. 1, we use Eq. 2 for the radius of curvature:
d x d s d 2 y = 2 c x .
We integrate with respect to x to get
d s d y = c x 2 Eq. 3
that satisfies the boundary condition of d y / d s = 0 at x = 0 . We can use the identity d s 2 = d x 2 + d y 2 again to express d x d y with d s d y :
d x d y = 1 − ( d y / d s ) 2 d y / d s
and use Eq. 3 to get
d x d y = 1 − c 2 x 4 c x 2 , or
d x ′ d y ′ = 1 − x ′ 4 x ′ 2 ,
if we introduce the scaled variables x ′ = c x and y ′ = c y . The solution is
y ′ = ∫ 0 x ′ 1 − η 4 η 2 d η
The result can be expressed in terms of elliptic integrals. The point x ′ = 1 corresponds to the middle point of the bow, d = 1 . The corresponding y ′ value is ℓ / 2
2 ℓ = ∫ 0 1 1 − η 4 η 2 d η = E ( − 1 ) − K ( − 1 ) ≈ 0 . 5 9 9 0 7
where K and E are elliptic integrals of the first and second kind, respectively. Therefore ℓ = 1 . 1 9 8 1 4 and the ratio of the two measurements is d / ℓ = 0 . 8 3 4 6