Bending A Triangle
Triangle A B C has coodinates A = ( − 4 , 0 ) , B = ( 4 , 0 ) , and C = ( 0 , 3 ) .
Let P be the point in the first quadrant such that △ A B P has half the area of △ A B C but both triangles have the same perimeter.
What is the length of C P ? If your solution is in a form of d , submit d as the answer.
The answer is 21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is an unusual approach. Thanks for sharing =D
Wait... Why must the point P lie on the ellipse as well? Why can't it be inside (or outside) the ellipse?
Log in to reply
For any point P on the ellipse graph and two foci points F 1 & F 2 , the sum of P F 1 + P F 2 is always constant. If point P is not on the ellipse graph, the perimeter of △ A B P will no longer equal to that of △ A B C .
Log in to reply
You didn't answer my question. I asked why must P lie on the ellipse as well. Your explanation was that "because it's in the ellipse, then this condition must hold".
Log in to reply
@Pi Han Goh – I think I already answered the question quite directly. If it's not on the ellipse, the perimeter will change. (Can you find any other point P not on the ellipse that satisfies the condition then?)
Log in to reply
@Worranat Pakornrat – Great. I think it's better to add that to your solution (1st paragraph) to make it more explicit. Thanks.
I did this. @Pi Han Goh it's because any point on an ellipse, when its distances from the foci are added, will always be constant. In order for the perimeter to be the same, it has to have the point on the ellipse.
I had it the same approach because I remembered the ellipse definition but Saad approach below is simpler.
You are fine Mr.ahmad saad Good solution
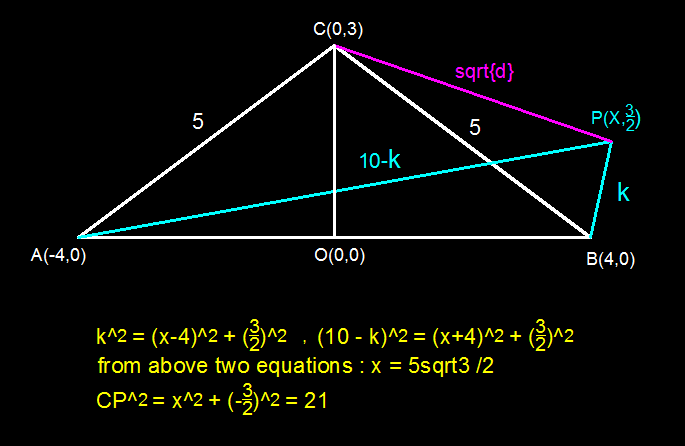
How to get x value
Log in to reply
Distance between two points P(x1; y1) and Q(x2; y2) is given by:
d(P;Q) = sqrt{(x2 −x1)2 + (y2 −y1)2} ............. (Distance formula)
my understanding is that the triangle having the same perimeter meant all points (corners) of the triangle fit in the circle. Hence had a solution of 12.5 the origin of this circle is at (0 , -7/6)
Since △ A B C and △ A B P share the same base A B and have the same perimeter, we can fix the points A & B as the foci and attach imaginary threads to draw an elliptical curve as shown below:
For any point P on the ellipse graph and two foci points F 1 & F 2 , the sum of P F 1 + P F 2 is always constant. If point P is not on the ellipse graph, the perimeter of △ A B P will no longer equal to that of △ A B C .
In this case, the total distance of A C + C B (blue) = distance of A P + P B (red), and we can formulate the graph as: a 2 x 2 + b 2 y 2 = 1
Then the focal length is half of A B = 4 , and b is the height of △ A B C = 3 . Then a 2 − b 2 = 4 2 ; a 2 = 3 2 + 4 2 ; a = 5 .
Therefore, the formula for this ellipse is 5 2 x 2 + 3 2 y 2 = 1 .
Since the area of △ A B P is half of the △ A B C , the height (also the distance from the x -axis) is half of the original one; the height is 2 3 , which is the y value.
Plugging in this y value, we will get y 2 = ( 2 3 ) 2 = 4 9 :
5 2 x 2 + 3 2 4 9 = 1 ; x 2 = 4 7 5
As a result, the distance of C P = 4 7 5 + ( 3 − 2 3 ) 2 = 4 7 5 + 9 = 2 1 .