Between parabolas
A figure is constructed from two parabolas with vertical axes of symmetry and distinct vertices. The parabolas intersect through each other's vertices. The figure is contained by horizontal segments that go through the parabolas' vertices.
What fraction of the figure's area is the area bounded by the two parabolas?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Moderator note:
It should be noted the 3 2 ratio also holds for parallelograms, not just rectangles.
Could you care to elaborate how the parabola fill 2/3 of rectangular. I seemed to forget everything I have learned in school. I solved this question only assume that parabola is made from f(x)=4*x^2. I need a universal solution.
Log in to reply
Let the equation of parabola be x^2=4y. Consider the rectangle bounded by x=0to2 and y=0to1. Area of this rectangle = 2. Area under parabola within the rectangle = ∫ 0 2 y d x = ∫ 0 2 ( x 2 / 4 ) d x = 2/3. Required area = 2-2/3 = 4/3. So you can see that 4/3 is 2/3rd of 2.
Archimedes figured out the 2/3 ratio and almost used calculus. I decided to use this fact in my solution but put the category as calculus. Other solvers prove this via integration.
I did not understand the question.
Parabolas with vertical axis of symmetry are of the form y = (x-a)^2 for some real number a.
How is it possible for them to have an area of intersection?
Let the parabolas be x 2 and 2 x − x 2 , so that the vertices are ( 0 , 0 ) and ( 1 , 1 ) . Since only the relative areas matter, the exact choice is irrelevant and this is the easiest.
The area of overlap is then ∫ 0 1 ( ( 2 x − x 2 ) − x 2 ) d x = 3 1
While the entire area is ∫ − 1 0 ( 1 − x 2 ) d x + 1 + ∫ 1 2 ( 2 x − x 2 ) d x = 3 7
The ratio is therefore 7 1
It's a cleaver solution :). But i would argue that this does not prove the case in general. I used $f(x) = ax^2$ and $g(x) = -ax^2 + bx$ and then perform the same calculations. I then get $|A| = \frac{d^3}{24a^2}$ and $|B| = \frac{7d^3}{24a^2}$, where $|A|$ the area of the figure and $|B|$ is the area of the overlap. It is then seen that the constants cancel when computing the fraction $|B|/|A|$ and you get $\frac{1}{7}$ out .
Log in to reply
How to write in math mode by the way :D??...
Log in to reply
To write it in LaTex, simply replace your first $ by backslash followed by open parentheses and the second $ by backslash followed by close parentheses. If you want more on the system, pretend to start writing a new problem and the instructions will be provided to you. Below is how you post would look then:
I used f ( x ) = a x 2 and g ( x ) = − a x 2 + b x and then perform the same calculations. I then get ∣ A ∣ = 2 4 a 2 d 3 and ∣ B ∣ = 2 4 a 2 7 d 3 , where ∣ A ∣ the area of the figure and ∣ B ∣ is the area of the overlap. It is then seen that the constants cancel when computing the fraction ∣ B ∣ / ∣ A ∣ and you get 7 1 out .
Log in to reply
@Marta Reece – Nice, thanks a lot for the help ∀ ε > 0 ∃ N ∈ N ∀ n ∈ N : n ≥ N ⇒ ∣ r − a n ∣ < ε
It does prove it in general, since we are only interested in the ratio of areas, which is conserved when doing any linear transformation. And the general case can be arrived at from my specific one by such transformation.
Let the intersection points be ( 0 , 0 ) and ( 1 , 1 ) . Note that the equation of the downward-pointing parabola can be written as y = x 2 and the equation of the upward-pointing parabola can be written as y = 2 x − x 2 . The area of intersection is:
∫ 0 1 ( 2 x − x 2 − x 2 ) d x = ∫ 0 1 ( 2 x − 2 x 2 ) d x = [ x 2 − 3 2 x 3 ] 0 1 = 1 − 3 2 = 3 1
Note that the area bounded by the y-axis, the line y = 1 and the graph y = x 2 is equal to ∫ 0 1 y d y . Considering that this area is equal to that bounded by the x-axis, the line x = 1 and the graph y = 2 x − x 2 , the total area is:
1 + 2 ∫ 0 1 y d y = 1 + 2 [ 3 2 y 3 ] 0 1 = 1 + 2 ( 3 2 ) = 1 + 3 2 × 2 = 1 + 3 4 = 3 3 + 4 = 3 7
Finally the desired fraction is 7 1 .
Is it not possible that y=ax^2 with a > 0 is considered as a parabola with (0,0) as lowest point? I know the end result is the same, but I'm curious about what can be considered as parabola in Cartesian diagram.
One of the parabolas is not necessarily
y
=
x
2
. I'm going to use more general equations. Let the intersection points be (0,0) and (h,k).
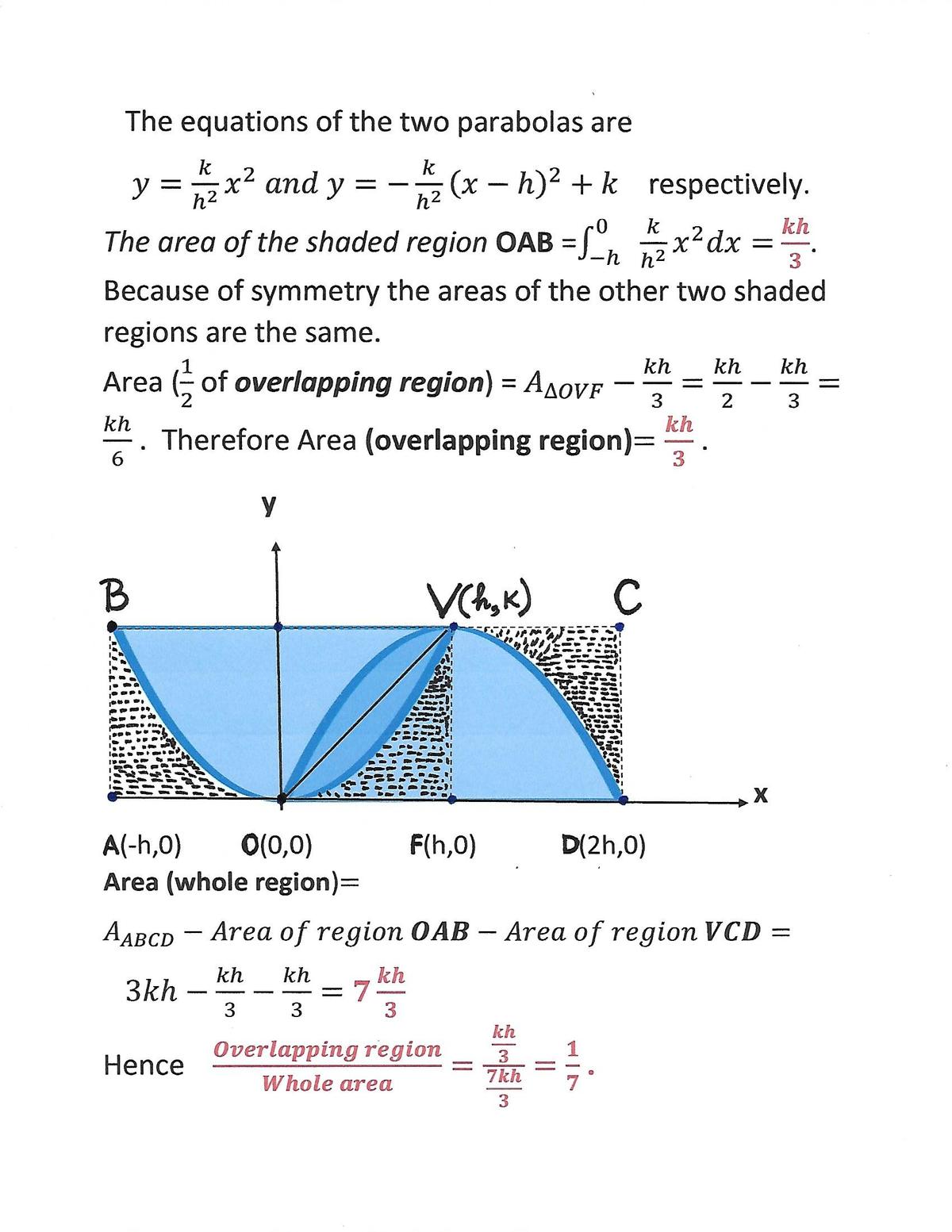
This answer needs more upvote
0 ∫ 1 x 2 d x = 3 1
Drawing it out:
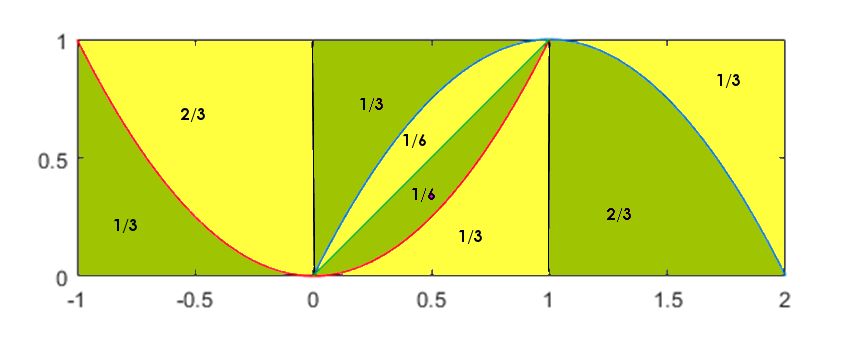
So adding up the areas:
(1/6+1/6)/(2/3+1/3+1/6+1/6+1/3+2/3) = 1/7
Very nice!!!
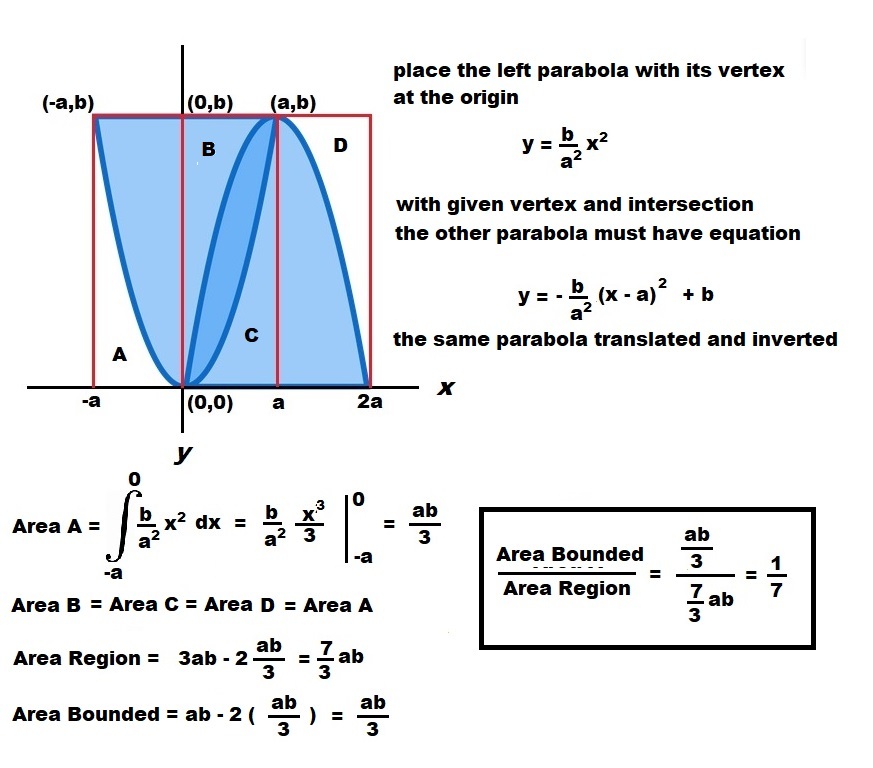
Let the left parabola be y = k x 2 which k > 0 , and it intersects another parabola at points ( 0 , 0 ) and ( a , k a 2 ) , the another parabola can be expressed as y = − k x 2 + 2 a k x . Let the area at the middle be B , and the area enclosed by a parabola and horizontal line be A , so the full figure is 2 A − B . B = ∫ 0 a ( − k x 2 + 2 a k x ) − ( k x 2 ) d x = 3 1 a 3 k
A = ∫ 0 2 a − k x 2 + 2 a k x d x = 3 4 a 3 k From the result we see that A = 4 B , so the ratio is 2 A − B B = 8 B − B B = 7 1
I solved this by mentally visualizing different types of parabolas, stretched and narrow and finding out via intuitive cluster-data analysis what the approximate fraction would be.
1) Divide the area. It's seen that the whole area is 2 triangles plus the area in the middle.

2) The middle area
A
m
i
d
d
l
e
=
A
p
a
r
a
b
o
l
a
−
A
t
r
i
a
n
g
l
e
Figure out the area between the red curve and y-axis.
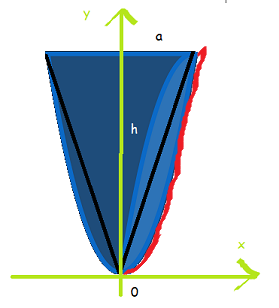 An inverse function is needed:
y
=
c
x
2
becomes
x
=
y
/
c
(when
x
is positive)
An inverse function is needed:
y
=
c
x
2
becomes
x
=
y
/
c
(when
x
is positive)
Integrate and multiply by 2 to get both sides. A p a r a b o l a = 2 ∗ ∫ 0 h ( y / c ) d y = 3 c 4 ∗ h 2 3
Area of the triangle A t r i a n g l e = a h . But also a = h / c , so A t r i a n g l e = c h ∗ h = c h 2 3
The middle area is A m i d d l e = A p a r a b o l a − A t r i a n g l e = 3 c 4 ∗ h 2 3 − c h 2 3 = 3 1 ∗ c h 2 3
2 ∗ A t r i a n g l e + A m i d d l e A m i d d l e = 3 7 3 1 = 7 1
It can be solved with simple calculus. Calculate the C area between the curves a(x) = x^2 and a inverted down replica of it intersecting its vertice. It might be something like b(x) = -(x-2)^2 + 4. The B area (above this function "b") added to the area between y=4 and the initial "a" parabola minus the area between both the curves is going to be the total area. Dividing that C area by the Total area will give you the ratio between them.
I cheated a bit by measuring the width and height of the parabolas. It turns out they have a width of 3 and a height of 9. The left parabola is the graph of the function: f(x)=x^2 . The right one has the corresponding function: g(x)=-x^2+6 x . For the intervall {0;3} : g(x)≥f(x) . Therefore our d(x) is equal to: g(x)-f(x) . d(x)=-2 x^2+6 x By taking the integral of d(x) in the intervall {0;3} we find out the overlapping area is equal to 9. In order to find out the area of the entire figure I first changed f(x) into f2(x)=x^2-9 This makes it easier to get the area within one parabola. The area of one is 36. Hence both parabolas are congruent to each other, the are of the entire figure is: A(whole)=A(parabola) 2-9 . We have to subtract 9 in order to make sure we only take the overlapping area once. In the end you divide the overlapping area by the entire are and 9/63 equals 1/7 . I apologize for bad use of english technical terms and technical spelling. I am not a native speaker. Thank you!
Good idea. When a problem implies the solution is unique but does not give the value of a certain parameter, it is a sneaky idea to set it to some value. In this case, since all parabolas are similar, you are more than justified.
Use parabola y=4x^2 and parabola y=1-4(x-1/2)^2 to find the overlap area of two parabolas as 7/6. The intersection area of two parabolas is equal to 1/6, which gives the desired ratio as equal to 1/7.
It is well known that a parabola fills 3 2 of the rectangle that contains it. WLOG let each of the three rectangles have area 3 . The entire shaded area is then 2 + 3 + 2 = 7
Intersection area is 1 .
The proportion is 7 1