BFraction
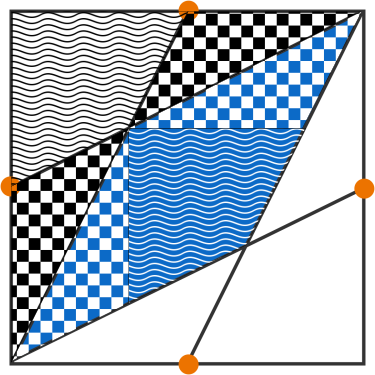
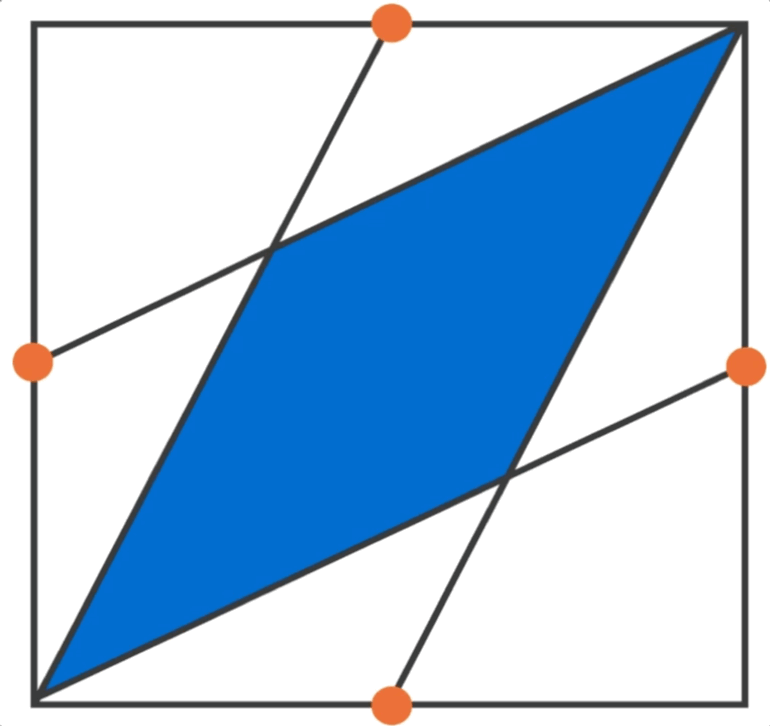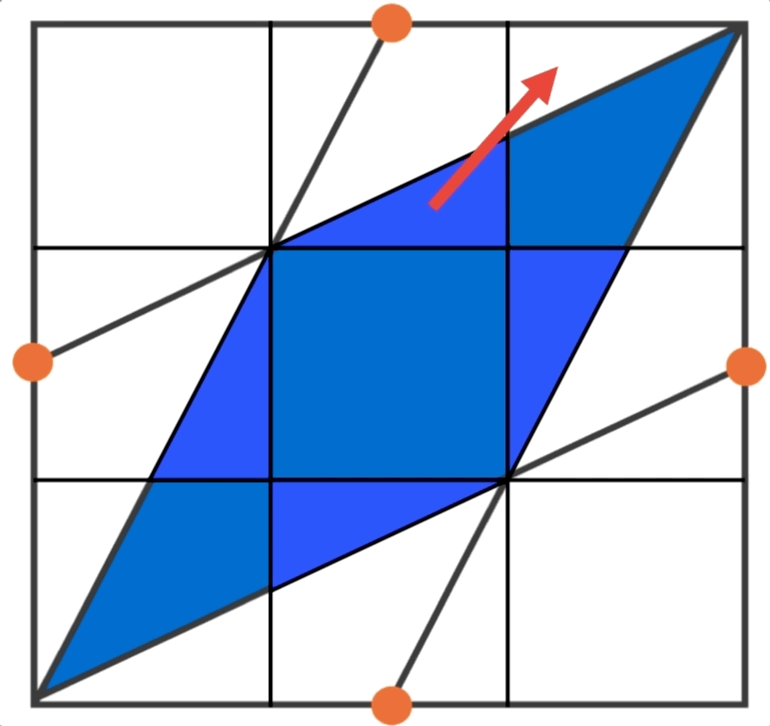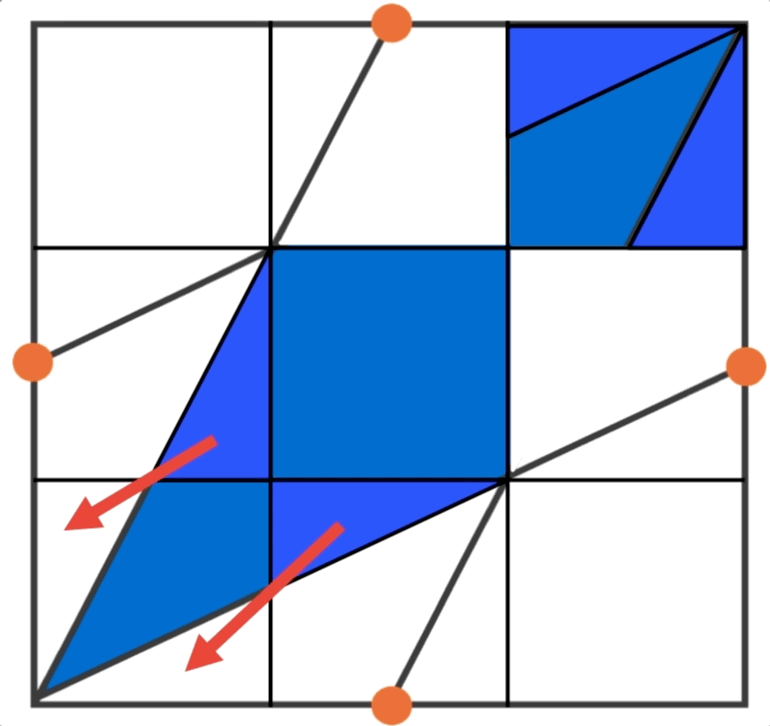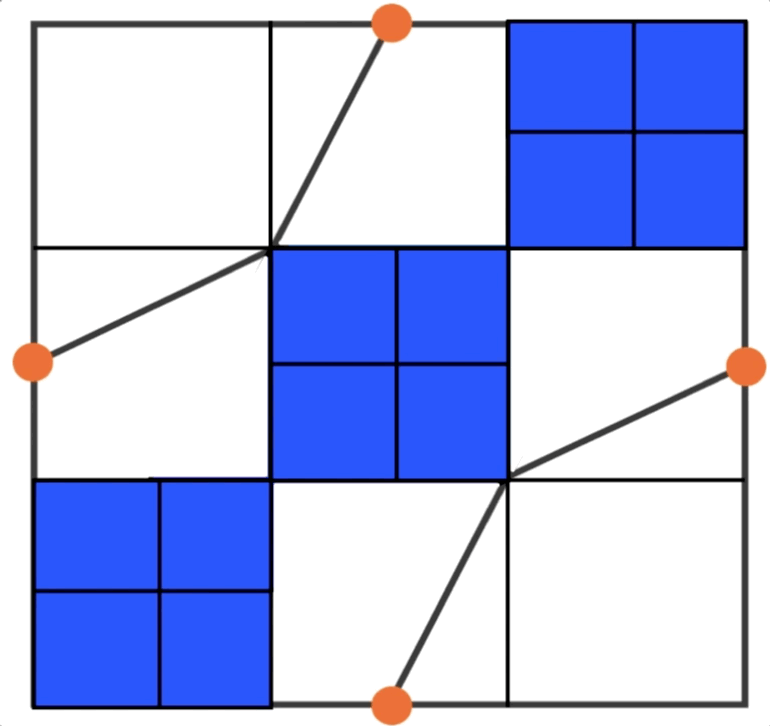
The orange points are the midpoints of the sides of a 6 × 6 square.
What is the area of the portion shaded blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
23 solutions
So tricky a question!the answer was fabulous
Very elegant approach, thanks for the insight!
Yeah... I still have a long way to go in math. Ty for the answer.
no way,, median
MN = AM/3 would not be the case if Triangle BAC wasn't a right angle isosceles with Angle BAC as the right angle...
Log in to reply
It's given that ABDC is a square.
Log in to reply
i get that, but the explanation gives the impression that this applies to all triangles
Log in to reply
@Mark Ch'n – M N = 3 1 A M is true for all triangles if A M is a median, A is a vertex, and N is a centroid. "The centroid divides each median into two parts, which are always in the ratio 2 : 1 " ( https://brilliant.org/wiki/triangles-centroid/ )
The shortest diagonal of the blue parallelogram is 1/3 of AD. If you cut the parallelogram in half through AD, you end up with 2 triangles with base AD/3 and height AD/2. So area is AD/3 * AD/2. AD = sqrt(6^2 + 6^2) = sqrt(72) Area = sqrt(72)/3 * sqrt(72)/2 Area = 12
Relevant wiki: Basic Composite Figures
Let's place the 6 by 6 square on a coordinate grid with C at ( 0 , 0 ) .
Notice that the slopes of the line segments connecting midpoints are 3 6 , 6 3 , − − 3 6 , and − 6 3 so they reduce to 1 2 , 2 1 , − 1 2 , and − 2 1 respectively. This means we know they pass through the marked red points on the grid.
We can now use the formula 2 1 b h for the area of a triangle to find the area of four of the triangles:
Since the area of the square is 6 × 6 = 3 6 , subtracting the triangle areas gets us the central shape area of 3 6 − 9 − 9 − 3 − 3 = 1 2 square units.
Moderator note:
As pointed out in the comments, a possible alternate continuation would be Pick's Theorem, which uses the points of the graph paper to figure out the area.
Wiki page about Pick's Theorem here
We also have a three part series in our Out of the Box Geometry course which leads through Pick's Theorem.
After investing time in drawing on the grid you could just use Pick's theorem.
Log in to reply
Indeed (although for a Basic 3 problem I won't assume our audience knows it, even though I did write a part of a course which covers it specifically).
If I had invested time drawing on the grid I couldn't have used Pick's theorem because I've never heard of it (or possibly forgotten it). You may know your maths, but your logic sucks.
Incidentally, this is the method I used.
Log in to reply
My comment was addressed to Jason Dyer who knows the theorem. There is no reason to be offended.
Log in to reply
@Alex Simkin – I'm sorry, I didn't know you knew Jason Dyer.
I also used the same method of the coordinate grid but then found the diagonals of the parallelogram and used A = 2 d 1 × d 2 , I thought that was a bit easier.
Relevant wiki: Basic Composite Figures
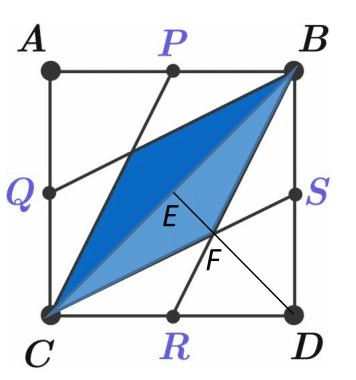 Blue region consists of two identical triangles.
△
B
C
F
has a base
B
C
=
6
2
.
Blue region consists of two identical triangles.
△
B
C
F
has a base
B
C
=
6
2
.
From symmetry, line E D is perpendicular to it, so the height of the triangle is E F .
Since E D , B R , and C S are medians, their intersection F splits each of them in 2 : 1 ratio and E F = 3 1 ⋅ E D = 6 1 ⋅ A D = 6 1 ⋅ 6 2 = 2
The blue area is 2 times the area of triangle B C F , that is 2 ⋅ 2 1 ⋅ 6 2 ⋅ 2 = 1 2 .
That is the most simplistic approach I've seen towards solving this problem.
I tried to measure the blue area but I didn't really understand it. I don't really get how the problem works that well. I would rate this problem a 10 because I didn't get it.
I did it whit three integrals
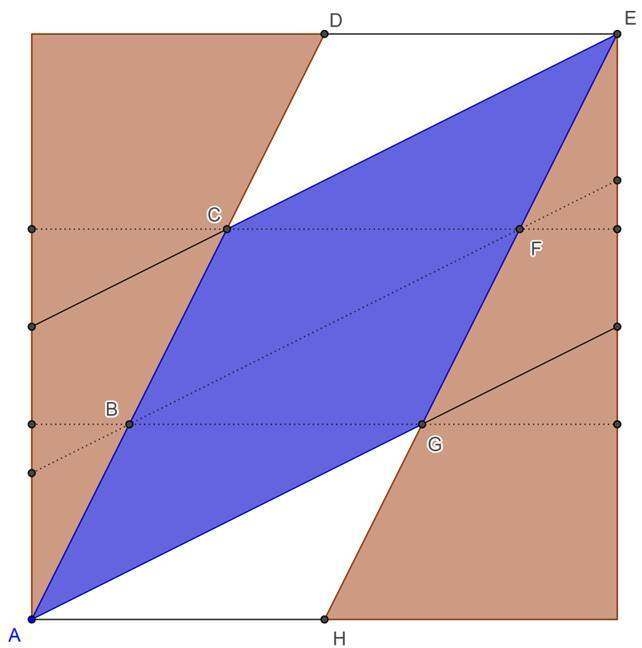
By observation, we can see that the 2 brown triangles make up half the area. Meaning that the parrellogram ADEH is half the area of the original square.
Parallel to DE, construct a line through point C. The intersection of this parallel line and EH is point F. Parallel to DE, construct a line through point G. The intersection of this parallel line and AD is point B. Parallel to CE, construct a line through point B. We see that this parallel line through B intersects EH at point F.
This implies that A B = B C = C D and H G = G F = F E
The parallelogram ADEH is now divided into 6 congruent triangles, 4 of which make up the required area.
Hence, area shaded blue 2 1 * 6 2 * 6 4 = 12
This was nice and easy to understand, thank you
By far the best solution!
Clever! Is the reason that the line parallel to CE, through B, intersects EH at exactly the same place that the line parallel to DE, through C, does due to BC being parallel to EF?
Log in to reply
Hi Don, thank you for the encouragement! Thank you for your question as it made me think more deeply on this.
I reconstructed the original question for the cases where the main shape (which is a square in the original question) is a generic parallelogram, trapezium or a generic convex quadrilateral. I found that my solution only holds true for cases where the main shape (and hence the blue shaded region as well) is a parallelogram.
Hence, the fact that the blue shaded shape is a parallelogram (and thus, the assumption in your question) is a necessary condition.
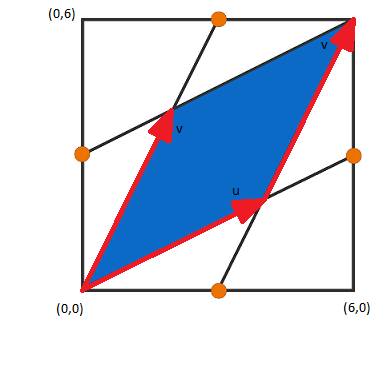
Let's draw the vectors u and v . It is clear that these vectors are respectively proportionnal to (2,1) and (1,2), hence u = c ⋅ ( 2 , 1 ) and v = c ⋅ ( 1 , 2 ) .
We can also see that u + v = ( 6 , 6 ) , hence c = 2 .
We eventually get that the area ( A ) is the norm of the cross product of these two vectors in a 3D space, we thus get:
A = ∣ ∣ ( 4 , 2 , 0 ) × ( 2 , 4 , 0 ) ∣ ∣ = 1 2
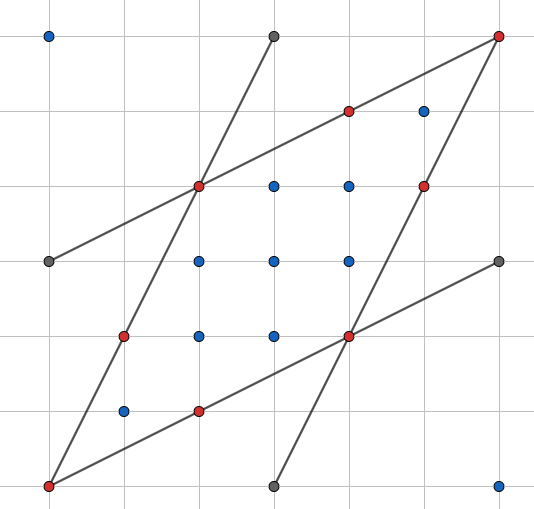 Pick's theorem: 9+
2
8
-1 = 12
Pick's theorem: 9+
2
8
-1 = 12
Very creative way to explain
We can easily see, that the blue area is exactly one third of the square.
By shifting the kite shape from the upper left corner to the center and by rotating the two congruent triangles by π , we find, that they exactly fill up the blue area. Because of the symmetry, the upper left white, the blue and the lower right white areas thus are the same.
 The kite shape and the two triangles exactly fill up the blue area.
The kite shape and the two triangles exactly fill up the blue area.
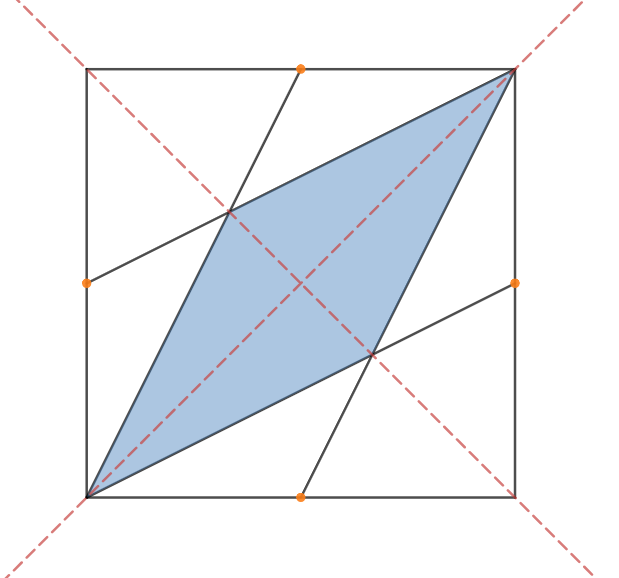
When plotted on a graph, the problem shown has axes of symmetry along
y
=
x
and
y
=
−
x
+
6
. When cut, it looks like this:
 We can use one of these cut blue sections to find a partial answer using the formula for the area of a triangle
A
=
2
1
b
h
, then multiplying by 4 to get our final answer. We'll be using the bottom-most section for this solution.
The lines that intersect the width of the blue shape can be expressed as
y
=
2
1
x
and
y
=
2
x
−
6
. We can find the point of intersection using simple algebra:
2
1
x
=
2
x
−
6
x
=
4
x
−
1
2
3
x
=
1
2
x
=
4
then substituting for
x
:
y
=
2
1
(
4
)
y
=
2
By intuition, the point of intersection of the axes of symmetry can be found to be at the center of the square, at
(
3
,
3
)
.
Now that we know what the first point of intersection is, we can use the
y
values of these points to find the area of the cut blue section:
A
=
2
1
(
6
)
(
3
)
−
2
1
(
6
)
(
2
)
=
2
1
(
6
)
(
3
−
2
)
=
2
1
(
6
)
=
3
Final answer:
3
∗
4
=
1
2
We can use one of these cut blue sections to find a partial answer using the formula for the area of a triangle
A
=
2
1
b
h
, then multiplying by 4 to get our final answer. We'll be using the bottom-most section for this solution.
The lines that intersect the width of the blue shape can be expressed as
y
=
2
1
x
and
y
=
2
x
−
6
. We can find the point of intersection using simple algebra:
2
1
x
=
2
x
−
6
x
=
4
x
−
1
2
3
x
=
1
2
x
=
4
then substituting for
x
:
y
=
2
1
(
4
)
y
=
2
By intuition, the point of intersection of the axes of symmetry can be found to be at the center of the square, at
(
3
,
3
)
.
Now that we know what the first point of intersection is, we can use the
y
values of these points to find the area of the cut blue section:
A
=
2
1
(
6
)
(
3
)
−
2
1
(
6
)
(
2
)
=
2
1
(
6
)
(
3
−
2
)
=
2
1
(
6
)
=
3
Final answer:
3
∗
4
=
1
2
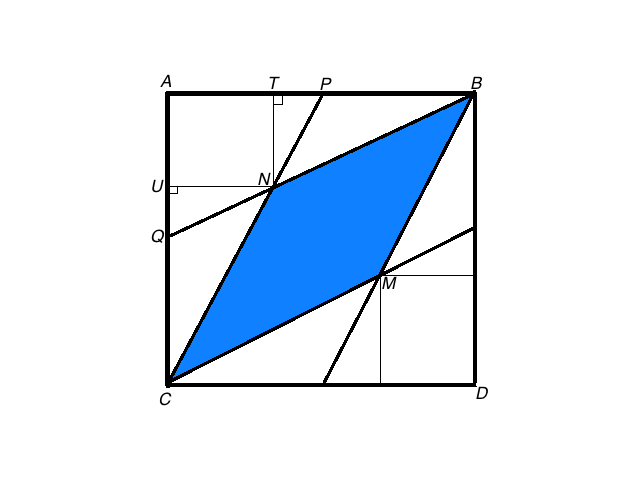
ABDC is a rectangle. PC bisects AB and QB bisects AC.
Draw perpendiculars from N to AB and from N to AC. Label their intersections with AB as T and with AC as U.
Triangles ABQ and TBN are similar (right) triangles, because they share a common angle at B.
Therefore, length(TB) / length(TN) = length(AB) / length(AQ) = 2.
Triangles APC and TPN are also similar (right) triangles, because they share a common angle at P.
Therefore, length(TN) / length(TP) = 2.
Multiplying these ratios, length(TB) / length(TP) = 4.
Therefore, length(TP) + length(PB) = 4 length(TP), so length(PB) = 3 length(TP).
Because length(AB) = 2 length(PB), length(AB) = 6 length(TP).
Because length(AB) = 2 length(AP), length(AB) = 3 length(AT).
By the same reasoning, length(AC) = 3 length(AU).
Therefore, using formulas for areas of squares and right triangles, area(ABDC) = 9 area(ATNU) = 9 area(TBN) = 9 area(UCN).
Adding the areas of non-overlapping figures, area(ABDC) = 3 area(ABNC).
By the same reasoning, area(ABDC) = 3 area(CDBM).
Thus, because the blue region in the problem does not overlap the two white regions, area(ABDC) = 3 area(CNBM).
In this case, area(CBNM) = 1/3 of (6 x 6), or 12.
This solution is based only on proving triangles with equal angles are similar and on the equality of ratios of lengths of sides of similar triangles. It does not depend on rectangle(ABDC) being a square. In fact, this solution generalizes to any parallelogram, and possibly to every convex quadrilateral, by constructing the line segments NT and NU parallel to the sides of the parallelogram or quadrilateral and adding the formula for the area of a parallelogram.
The area of
△
A
C
I
is equal to
△
A
C
D
−
(
△
C
E
I
+
△
A
D
E
)
.
Since the area of △ A C D = 1 8 and area of △ A D E = 9 , we need to find the area of △ C E I
The ∠ D C G = arctan ( 3 / 6 ) = α .
As △ C D G is rectangle, we know that ∠ D G C = π / 2 − arctan ( 3 / 6 ) = π / 2 − α . Then ∠ C E I = π − ∠ D G C = π / 2 + α
From sinus law in triangle we can deduce: S = 2 sin ( π / 2 + 2 α ) ∣ E C ∣ 2 sin ( α ) sin ( π / 2 + α ) = 1 . 2 3 . 6 = 3
Then we conclude than the area of the blue portion is: 2 ( 1 8 − 9 − 3 ) = 1 2
If a is the area of a triangle then we can write this square as 12 triangle .then 12a=36 implies a=3.Now the blue region can be wrriten as 4 triangle then the area of region is 4*a=12
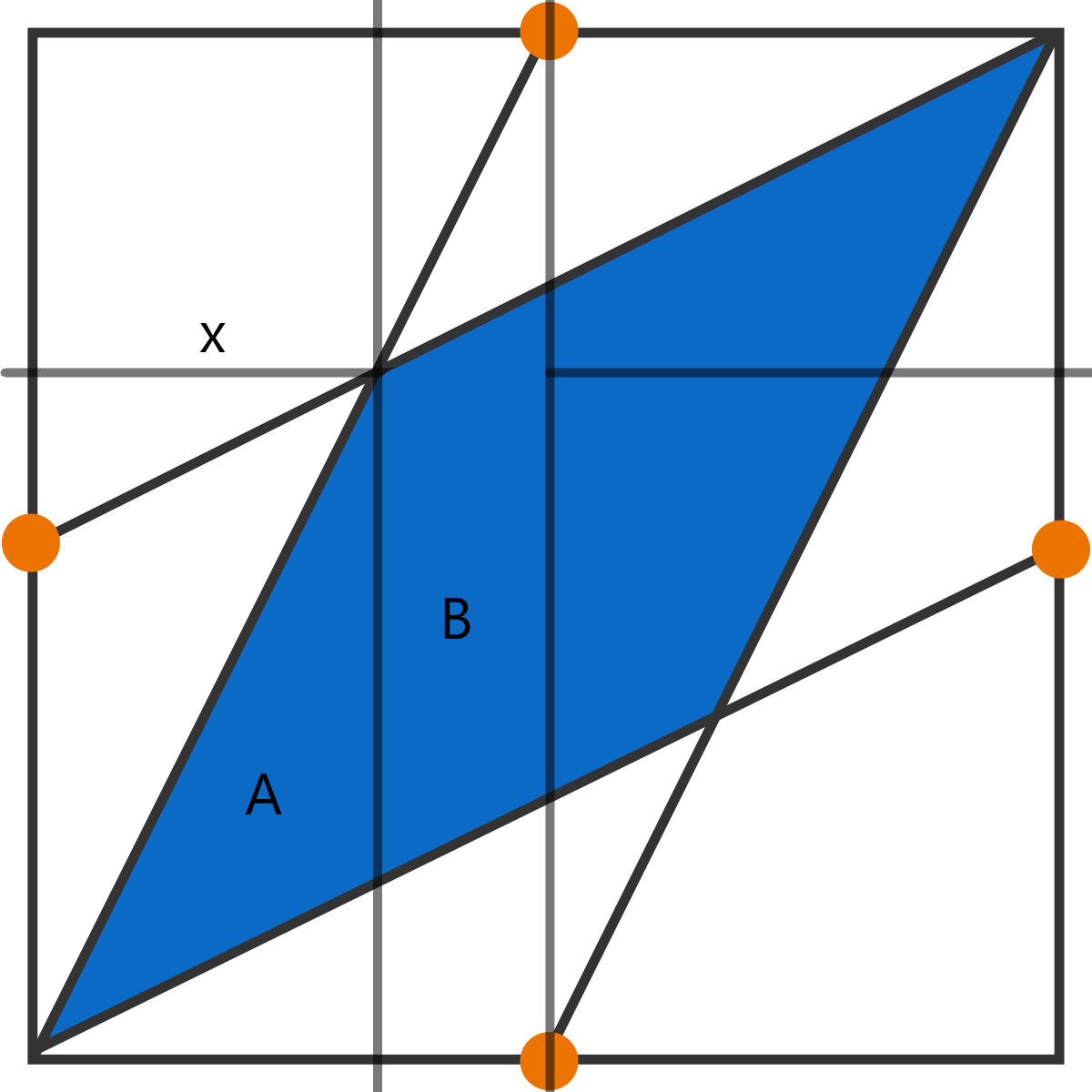
x L − x = 2 ⇔ x = 3 L
Where L is the length side. The blue area is then:
2 ( A + B ) = 2 ( 2 L × ( 2 x + ( 2 L − x ) ) ) = L × 2 L − x
Substituting x :
Area = L × 2 L − L / 3 = 3 L 2
For a length side L = 6 :
Area = 3 6 2 = 1 2
None except one of the answer is a multiple of 36. The blue are looks about a third of the square, so I guessed 12.
I imagined moving N to A and M to D, thus the blue area would be 100% of the square.
12 is the only divisor of 36 in the possível solutions list.
Area of ΔADF is 9. ΔAGJ and ΔGDJ have the same area because their bases AG and GD are congruent and they have the same height (segment JK). ΔGDJ ≅ ΔFDJ so ΔAGJ, ΔGDJ, and ΔFDJ all have the same area and their total area is 9 (ΔADF). Therefore each small triangle has an area of 3, and there are 8 small triangles (ΔAGJ, ΔGDJ, ΔFDJ, ΔCFJ, ΔCEI, ΔEBI, ΔHBI, and ΔAHI) for a total area of 24. The complete square has an area of 36.
36 - 24 = 12
In general, the area of shaded portion i.e. rhombus
= 3 1 ( area of square) = 3 1 ( 6 2 ) = 1 2
with the help of autocad drawing i could easily solve this problem. the ans is 12
Let A, B , C and D be the four corners of the square,
W, X, Y and Z be the centre of two corners (W = centre of AB, X = centre of BC, and so on),
And P and Q be the two corners of the blue region that is not touching the square. (P nearer to W and Z and Q nearer to X and Y)
The area of the blue region is four times as big as a triangle formed by - a corner of the square (e.g. A) - a point in the centre of two corners (e.g. W) - and the nearest corner of the blue region to them (e.g. P)
Parallelogram BYCZ is six times th triangle mentioned up there, and its area is equal to 3 × 6 which is 18.
Thus, the area of the blue region = 18 ÷ 6 × 4 = 12
6×6=36. A square has 4 sides the middle of the square would have to be an even number divisible by 6
No symbols solution: You can fit the top triangle, left triangle and bottom right quadrilateral in the central piece just with translation. That means that one white region has the same area as the blue region. Hence the blue region is a third of the whole area. 36/3=12
Let's start by drawing the diagonal A J
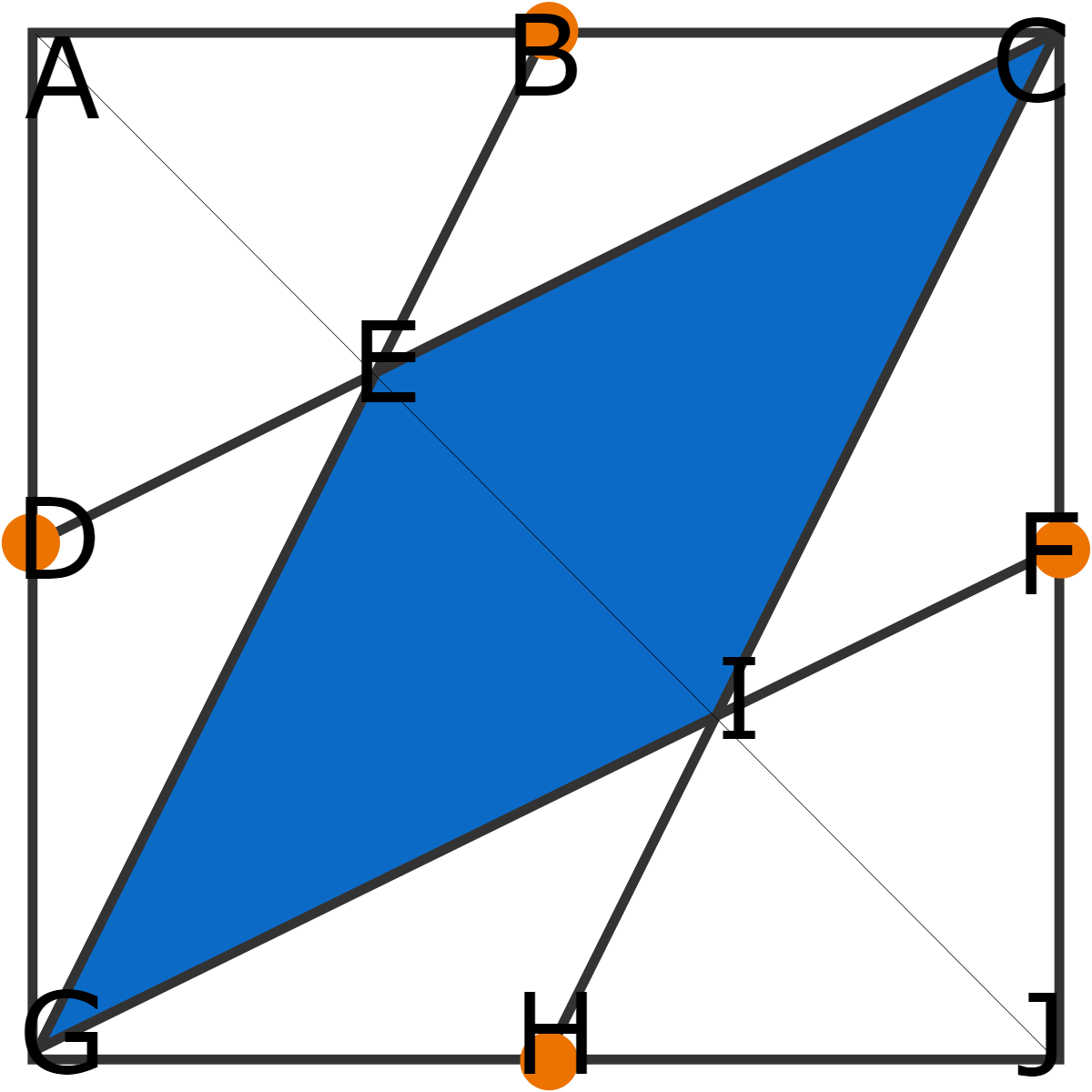
Since the equation of D C is y = 2 x + 2 1 and the equation of G B is y = 2 x
Set them equal to each other to find that they intersect at the value of 3 1
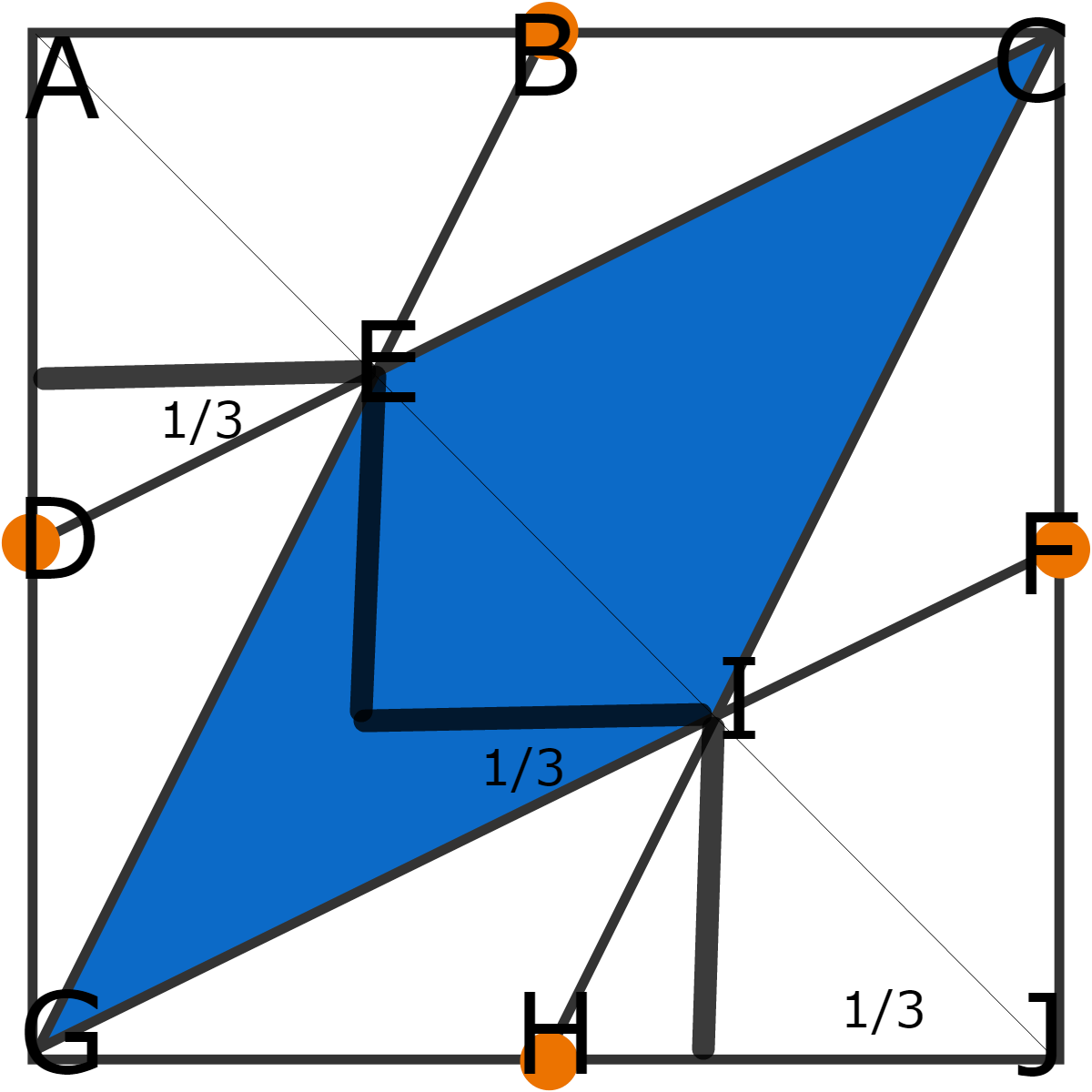
From this we can see that A E = E I = I J
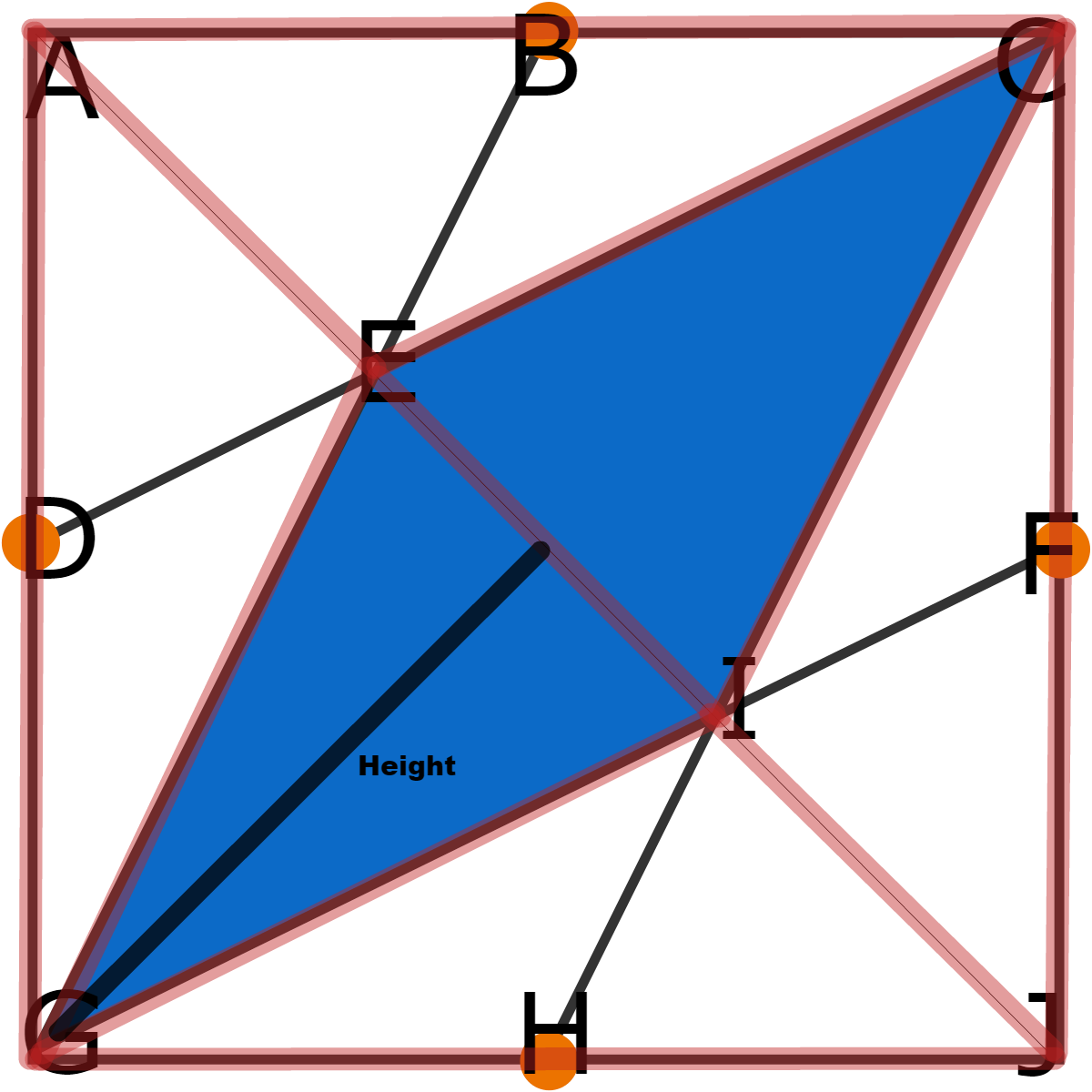
Break the figure into 6 triangles △ A E G △ E G I △ G I J △ A C E △ C E I △ C I J , since they all have the same base length and height their areas must be equal. Since this figure is made up of 6 of these triangles one of these triangles is 6 1 the area of the total square, since we have two triangles we have 6 2 of the area of the total square.
In this case the area is 3 6 so we multiply that by 6 2 and get the answer 1 2
Relevant wiki: Length and Area Problem Solving
Draw diagonals A D and B C , and let M be its intersection point, and let N be the intersection point of C P , B Q , and A D , as shown below.
Since C P , B Q , and A M are medians of △ A B C , N is the centroid, and therefore M N = 3 1 A M .
This means that △ M N B is 3 1 the area of △ M A B , and since A D and B C split the square and the blue portion into 4 congruent parts, by symmetry the blue portion is 3 1 the area of square A B C D .
Therefore, the area of the blue portion is 3 1 ( 6 ⋅ 6 ) = 1 2 .