Bigger, but how big? [Circles III]
How big is the red portion's area compared to the blue portion's area (only the closed broken-donut shape)? All angles that look perpendicular can be assumed as perpendicular, all lines that look like an unbroken line is a proper line, and all arcs that look like part of a circle, are part of a circle.
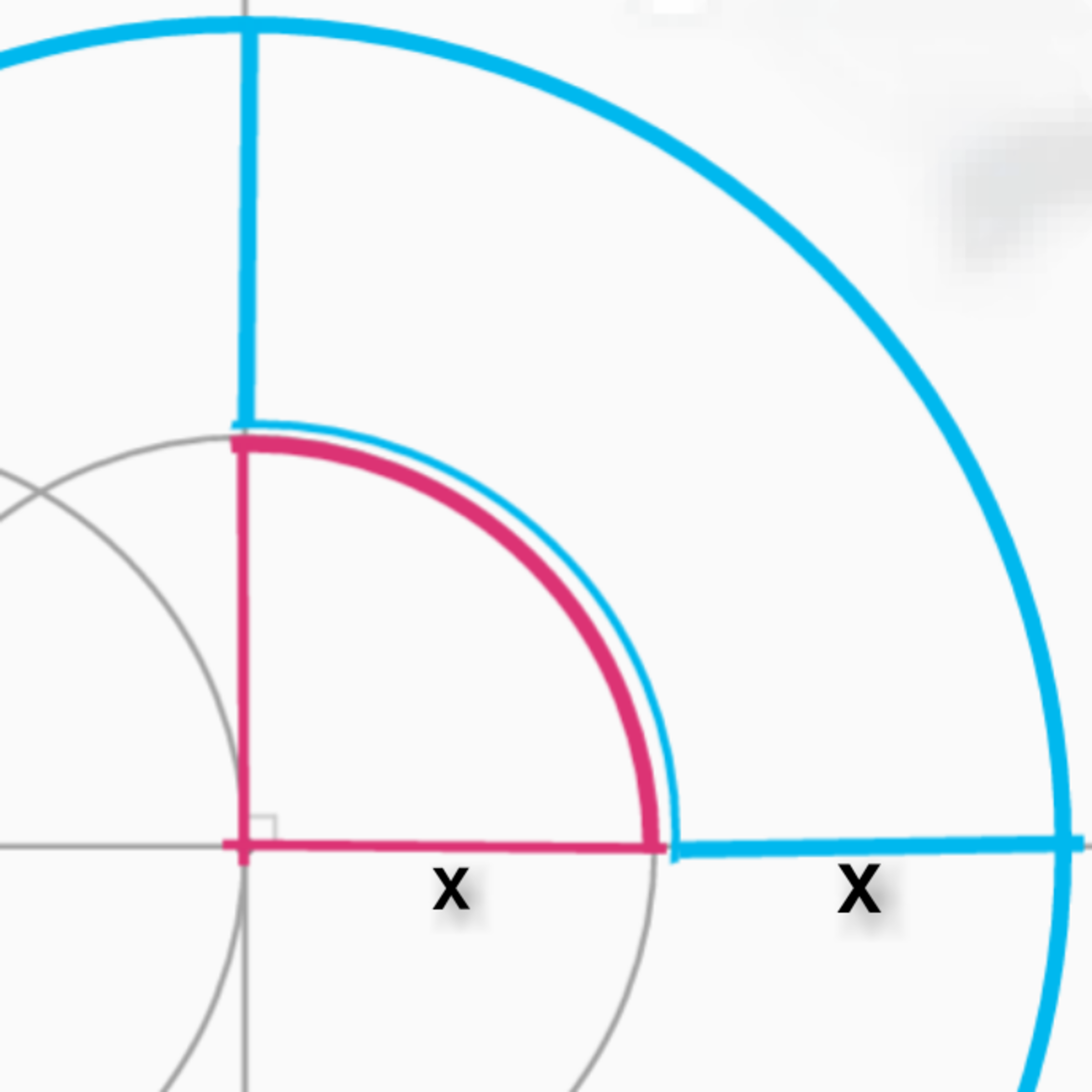
Type the comparison as a decimal, if it is 5 2 , type it as 0 . 4 0
Type recurring decimals with two decimal places. 7 1 can be typed as 0.14
It is the ratio of comparison, not the difference
Report area : The report room
The answer is 0.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Sometimes(rarely for me), even difficult ones are fun!
Log in to reply
I just posted this as a explanation as I have nothing to explain!
Log in to reply
Explanation Paradox?
\[ \begin{align} {\color{Red}{A_{\text{Quarter circle}}}} &= \dfrac{\pi x^2}{4} \\ \\ {\color{Blue}{A_{\text{Quarter donut}}}} &= \dfrac{\pi (2x)^2}{4} - \dfrac{\pi x^2}{4} \implies \dfrac{3 \pi x^2}{4} \\ \\ \dfrac{{\color{Red}{A_{\text{Quarter circle}}}}}{{\color{Blue}{A_{\text{Quarter donut}}}}} &= \dfrac{\frac{\pi x^2}{4}}{ \frac{3 \pi x^2}{4}} = \dfrac{1}{3} \approx \boxed{0.33}
\end{align}\]
A simple solution for a simple question. Thanks @Mahdi Raza !
Colorful solution! :)
Area of red = 4 π x 2
Area of blue = 4 π ( 2 x ) 2 − 4 π x 2 = 4 π ( 4 x 2 ) − 4 π x 2 = 4 π ( 3 x 2 )
Ratio of red to blue = 4 π ( x 2 ) ÷ 4 π ( 3 x 2 ) = 3 1 ≈ 0 . 3 3 (to 2 decimal places).
Thanks for trying out my question @Vinayak Srivastava !
Log in to reply
You're welcome! BTW, please add the word "ratio" as people might get confused!
Log in to reply
Added as you said. Thanks for the helpful suggestion!
Fun questions are not in the difficulty, but in the simplicity