Bigger they are, harder they fall.

If the 4th-best player makes it to the finals, then he will face the best player, as the best player never loses. That means somewhere in the first two rounds the 2nd-best player and the 3rd-best player had to be eliminated. Also, if the 4th-best player made it to the finals, he didn't face anyone higher than him in the first two rounds (or he would have been eliminated).

The 2nd-best player and the 3rd-best player cannot both be eliminated in the same round. If the 2nd-best player is eliminated, then he was playing the best player, and the 3rd-best player had to be playing someone worse than him and therefore advanced. If the 3rd-best player is eliminated, then he was either playing the best player, in which case the 2nd-best player was playing someone worse than him and advanced, or he was playing the 2nd-best player, in which case the 2nd-best player still advanced. That means the 2nd-best player and 3rd-best player had to eliminated in separate rounds, which means either: (A) the 2nd-best player was eliminated in the first round and the 3rd-best player was eliminated in the second round, or (B) the 3rd-best player was eliminated in the first round and the 2nd-best player was eliminated in the second round.

For (A) to happen, in the first round the 2nd-best player had to face the best player (out of 7 players to choose from), which is a $\frac{1}{7}$ chance, the 4th-best player had to not face the 3rd-best player (out of the 5 players left to choose from), which is a $\frac{4}{5}$ chance, and in the second round the 3rd-best player had to play the best player (out of 3 players to choose from), which is a $\frac{1}{3}$ chance, so $P(A) = \frac{1}{7} \cdot \frac{4}{5} \cdot \frac{1}{3} = \frac{4}{105}$ .

For (B) to happen, in the first round the 3rd-best player had to face the best player or the 2nd-best player (out of 7 players to choose from), which is a $\frac{2}{7}$ chance, the 4th-best player had to not face the 2nd-best player (out of the 5 players left to choose from), which is a $\frac{4}{5}$ chance, and in the second round the 2nd-best player had to play the best player (out of 3 players to choose from), which is a $\frac{1}{3}$ chance, so $P(B) = \frac{2}{7} \cdot \frac{4}{5} \cdot \frac{1}{3} = \frac{8}{105}$ .

The probability of either (A) or (B) happening is $P(A) + P(B) = \frac{4}{105} + \frac{8}{105} = \frac{4}{35}$ , so $a = 4$ and $b = 35$ and $a + b = \boxed{39}$ .

We will allocate each player to a position in the draw in a certain order which will make it easier to calculate (we don't need to worry about matching randomly after each round since this is equivalent to a draw position).

Firstly, note that the 4th best player will only make it through to the final if the 3 better players are in the other half of the draw. Also note that this entire tournament is trivial since the best player will always win!

Without loss of generality , allocate the 4th best player to a position in the draw. This doesn't affect the total number of possibilities so there are now $\color{#3D99F6}{7!}$ possibilities for the draw to result in, and we will see how many satisfy our condition.

• Allocate the 1st best player. There are $\color{#3D99F6}{4}$ satisfying positions (in the other half of the draw to the 4th best)
• Allocate the 2nd best player. There are $\color{#3D99F6}{3}$ remaining satisfying positions (again, in the other half of the draw)
• Allocate the 3rd best player. There are $\color{#3D99F6}{2}$ remaining satisfying positions (again, in the other half of the draw)

Now there are 4 players left (5th, 6th, 7th, 8th). It doesn't matter where they go, player 4 will still get to the final. These last four can be positioned in $\color{#3D99F6}{4!}$ ways.

Therefore the final probability is $\dfrac{4 \times 3 \times 2 \times 4!}{7!} = \dfrac{4}{35}$ so $a+b=\boxed{39}$

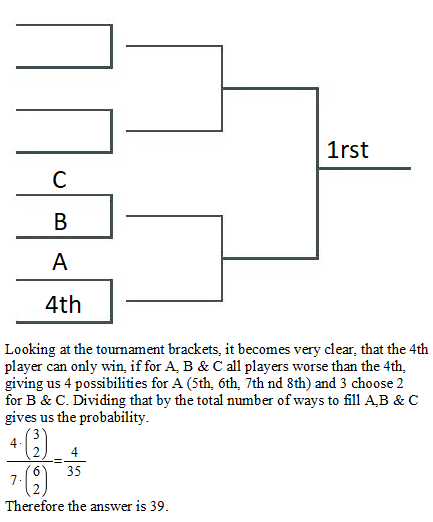
There are two brackets of 4 players. We are interested in number of distributions where none of #1, #2, and #3 are in the same bracket as in 4.

So the total number of distributions, we are picking 3 out of 7 players to be part of #4’s bracket. This would be 7!/(3!*4!) = 35.

Of those we have 4 cases which satisfy our condition, as 1,2,3 are already in the other bracket and we can put any of 5,6,7,8 in the last spot. (Once the bracket is all filled, there is only one option for the other bracket: everyone who is left)

So therefore, the probability comes out to be 4/35

The desired outcome:

Of the $7$ positions not taken by the #4 player, there are $4$ possible positions which we need the #1 player to land on. The probability of this is $\frac{4}{7}$ .

If this happens, of the $6$ positions not taken by the #4 & #1 players, there are $3$ possible positions which we need the #2 player to land on. The probability of this is $\frac{3}{6}$ .

Of the $5$ positions not taken by the #4, #1 & #2 players, there are $3$ possible positions which we need the #3 player to land on. The probability of this is $\frac{2}{5}$ .

The probability of all three conditions being met is $\frac{4}{7}\times\frac{3}{6}\times\frac{2}{5}=\frac{4}{35}$ , giving us $a+b=\boxed{39}$ .

One way to arrange this type of tournament is to randomly allocate each player one of the letters A to H. The matches then proceed according to a pre-determined protocol. Players A,B,C and D form one half of the draw and they play each other to produce one finalist. Players E,F,G and H are the other half of the draw and play together to produce the other finalist. Just a little thought will show that from this perspective player #4 will reach the final if and only if players #1,#2 and #3 are all in one half of the draw, and he is in the other half.

Once player #4 has been allocated a letter, there are 7 possible letters for #1, four of which are in the other half of the draw. So player #1 will land in the other half with probability $\frac{4}{7}$ . Now player #2 lands in the other half with probability $\frac{3}{6}$ , and finally #3 lands in the other half with probability $\frac{2}{5}$

Multiplying these together gives us our answer $\frac{4}{7} \times \frac{3}{6} \times \frac{2}{5}=\boxed{\frac{4}{35}}$

The probabilities are not changed if we draw up a blank programme of games (such as you get at the start of Wimbledon) and allocate all the first round games randomly. For the 4th best player to reach the final the top three players must be in the other half of the draw. The probablity of this is 4/7 x 3/6 x 2/5 = 4/35.

I don't know if I can express well how I reached the solution but I will try. So to make the forth player in the final he needs to avoid the 3 first players before the finale, hence they must be in the 4 spots of the other half. So the first player has a probabilty of 4/7 (the forth player has already his spot so only 7 are left and the first has to be in one of the 4 spots= 4/7), two spots being already taken the second player has a probability of 3/6=1/2 of avoiding the forth before the final. With the same logic the third player has a probabilty of 2/5 of avoiding the forth. So the probability for the forth to avoid the three first players before the final is 4/7 * 1/2 * 2/5=4/35. So a+b=4+35=39 I hope you understood!

There are three other players in the #4 player's half of the bracket, and for #4 to advance, each of those three players must be ranked either #5, #6, #7, or #8. The probability of this is 4/7 * 3/6 * 2/5 = 4/35. a+b=39.

Because the better player always win, if we divide the 8 players into 2 groups(4 players in each group), the odd of 4-th best player makes it to final is the same as 1st,2nd,3rd best player and 4-best player are in different group.

Let the best player belongs to group 1.

The probability of 2nd-best player also belongs to group 1 is $\frac{3}{7}$ . ( 3 slots are available in group 1 and 4 slots in group 2)

The probability of 3rd-best player also belongs to group 1 is $\frac{2}{6}$ . (2 slots are available in group 1 and 4 slots in group 2)

Now the probability of 4th-best player belongs to group 2 is $\frac{4}{5}$ .

Thus, it gives $\frac{3}{7}\times\frac{2}{6}\times\frac{4}{5}=\frac{4}{35}$ .

Since this is a single elimination 8-player tournament, for 4th-seed to be in the finals, this means that 4th-seed's half of 4 players can only have lower seeded players.

The starting position of each player in the half is irrelevant (as 4th-seed will always top the half). Thus for the 3 remaining spots in the half, only players below 4th-seed can be considered (i.e. 5th - 8th seed => 4 choices).

First spot : 4th seed (probability = 1)

Second Spot : probabaility = $\frac{4}{7}$

Third Spot : probabaility = $\frac{3}{6}$

Fourth Spot : probabaility = $\frac{2}{5}$

The order in the other half is irrelevant.

Hence, $\frac{4}{7}$ x $\frac{3}{6}$ x $\frac{2}{5}$ = $\frac{4}{35}$

$a + b = \boxed{39}$

In order for the 4th-best player to make it to the finals, three things have to happen: (1) one of the top 3 players must be eliminated in the first round -- otherwise, in the second round the 4th-best player would have to play against one of those 3 -- this has a probability of 3/7 because the probability of the 1st ranked player going against the 2nd ranked player is 1/7, and this is true for each of the three possible pairings 1 vs 2, 1 vs 3, or 2 vs 3, all of which are mutually exclusive. (2) the 4th-best player has to play against a lower ranked person in the first round -- conditioning against the first event above, this now has a probability of 4/5 because there are 4 players ranked lower than the 4th-best player among the 5 remaining players (excluding the two higher ranked players that were matched in the last event and the 4th-best player themself), and then (3) two of the top 3 ranked players will definitely be going into the second round and the 4th-best player has to play the one player other than them -- this has a probability of 1/3 since there is one good option out of the three possible players they could play against.

So using the multiplication principle, after conditioning the probabilities on each of the events mentioned above respectively, we have: $\frac{3}{7} \cdot \frac{4}{5} \cdot \frac{1}{3} = \frac{4}{35}$

Imagine that we just draw 2 groups of 4 players.

Getting into finals <=> Being the best out of the 4 players. (Trivial)

Now just need to iterate all the scenarios of a drawing group for our player. 3 out of {1,2,3,5,6,7,8}.

p1=7x6x5

Now we need to iterate all the scenarios where our player is the best player of this group. It's equal to the combination of 3 players out of all the players who are worse than our player. 3 out of {5,6,7,8}.

p2=4x3x2

Then we just divide p2 by p1 to get p

p= $\frac{7x6x5}{4x3x2}$ = $\frac{7x5x3x2}{4x3x2}$ = $\frac{7x5}{4}$ p= $\frac{35}{4}$

Our solution is then 39.

The format presented here is a simple tree structure, with the no. of players being a power of two. ( $8 = 2^{3}$ ) Dividing the the players into groups of four, the 4th best player must have defeated the second best of the group. Since only the better player can win, all other players in the group of four must be of a lower rank i.e 5th, 6th , 7th or 8th, a total of 4 possible players.

This gives a total of $4 \times 3 \times 2 = 24$ possibilities for the 4th best player's group for him to be able to advance to the finals.

But there are a total of $7 \times 6 \times 5 = 210$ possibilities for the 4th best player's group regardless of whether he is able to advance to the finals.

Hence, the probability that the 4th player advances to the finals is $\frac{24}{210} = \frac{4}{35}$ .

Hence, $a = 4 , b = 35$ . Hence, $a + b = 39$ .

The probability of the 4th best player going through the first round is (4/7) as he can only defeat players 5 to 8. We then have to estimate the how the other players get through to the second round. After player 4 takes on a player (i.e. any of players 5 to 8) we’re left with 6 players. The total number of ways each of these 6 can play each other once is 15. (Let me know in the comments if this is unclear to you) That being said, player 4 will only get to the final if he meets the remaining players from players 5 to 8 ( they should be 3 now since one of them has already been eliminated by player 4). Thus, 2 of the remaining 3 have to meet. The total number of ways any of these 3 can meet is 3. Hence there’s a 3/15 chance that player 4 will face one of them in the second round. Player 4’s probability of reaching the final is 4/7 * 3/15 = 4/35. And 4 + 35 = 39.

In the first round the number of ways the tournament can happen is by choosing 4 pairs from the 8 players which is $\frac{\binom{8}{2} \binom{6}{2} \binom{4}{2} \binom{2}{2}}{4!} = 105$ ways. The number of ways that 4th best player cannot be eliminated:

Case 1: If the best player is paired with 2nd best player - then 3rd best player must be paired with either of 5th, 6th, 7th or 8th best players (4 ways), 4th best player must be paired with the remaining 3 of the 5th, 6th, 7th, 8th, and the remaining 2 will be paired with each other making $4 \times 3 \times 1 = 12$ ways.

Case 2: If the best player is paired with 3rd best player - then 2nd best player must be paired with either of 5th, 6th, 7th or 8th best players (4 ways), 4th best player must be paired with the remaining 3 of the 5th, 6th, 7th, 8th, and the remaining 2 will be paired with each other making $4 \times 3 \times 1 = 12$ ways.

Case 3: If 2nd best player is paired with 3rd best player - then the best player must be paired with either of 5th, 6th, 7th or 8th best players (4 ways), 4th best player must be paired with the remaining 3 of the 5th, 6th, 7th, 8th, and the remaining 2 will be paired with each other making $4 \times 3 \times 1 = 12$ ways.

which makes a total of 36 ways.

So the probability that 4th best player will not be eliminated in 1st round is $\frac{36}{105} = \frac{12}{35}$ .

Now for the second round similarly there are $\frac{\binom{4}{2} \binom{2}{2}}{2!} = 3$ ways the tournament can happen in the second round. And only 1 way 4th best player cannot be eliminated is when the best player is paired with remaining of 2nd best and 3rd best from the first round (notice that exactly one of 2nd best and 3rd best can reach the second round if 4th best player has to reach the second round) and 4th best player getting paired with the remaining of 5th, 6th, 7th, 8th (notice again that exactly one of these will reach the second round if 4th best player has to reach the second round).

Thus Pr(4th best player wins the second round | 4th best player reaches second round) = $\frac{1}{3}$ .

So Pr(4th best player reaching finals) = $\frac{12}{35} \times \frac{1}{3} = \frac{4}{35}$ . So $a = 4$ , $b =35$ and $a + b = 39$

Although not a solution, I want to say that this is common problem trying to measure the second best. A good question would be what is the least number of matches required to determine the second best player. Another good question would be the third best and so on.

The 4th player plays 3 people before the final. He must beat them, so they all must be worse, and there are 4 worse players. So the combinations of players he could play and win all matches is 4C3=4, and the total number of combinations with any other player is 7C3=35. So probability = 4/35, 4+35=39.

Think of the draw being pre-set but created at random. Then Player #4 has to be in a different half of the draw than players 1,2,&3 to reach the final. Without loss of generality, let us place player 4 in any half. Now the remaining 3 places have to be filled by 4 lower ranked players. Who are 5,6,7,&8. The probability of one of these lower ranked players taking the second slot in the same half as #4 is 4/7. Given that this happens, the probability that yet another lower ranked player takes the third slot in that half is 3/6. And give this, the probability that the last slot is also filled by the lower ranked player is 2/5. Hence probability that all slots in the same half as #4 are players ranked below him is 4/7x3/6x2/5= 4/35