Binomial

Let S be the Sum of Coefficients

S=(coef. of A + coef. B)^n

S=(1+1)^6

S= 2^6

S=64

nCr nC0 + nC1+ nC2 +......+ nCn = 2^n

@Ashtik Mahapatra Why did you write (a+b^6)? It looks like $a+b^6$ . I was absolutely sure that it is $(a+b)^6$ & I didn't go wrong. Edit the question immediately .

Well, we solve it using Pascal's Triangle . Make the triangle until its first six levels & add the sixth row which is

$1+6+15+20+15+6+1 =$ $\boxed{64}$ .

Use the pascal's triangle: { Sixth row }

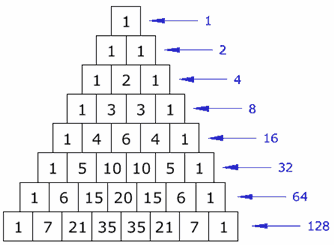
Solve it using pascals triangle 1 1 1 -> (a+b)¹ 1 2 1 -> (a+b)² 1 3 3 1..so on........ For (a+b)^6 ... The nos are
1 6 15 20 15 6 1... Sum of which is 64

there is a short-cut method for finding the sum of co-efficients in binomial... we can find it by putting all variables=1... so(a+b)^6 = (2)^6 = 64

by the law of pascel 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 so (1+6+15+20+15+6+1)=64

Use of the Pascal's Triangle helps to cap off.

Draw a pascal's Triangle and add all the numbers of line 6...Simplest way to do it..

Note that in expanding $(a + b)^6$ , we have:

$(a + b)^6 = a^6 + _6C_1 a^5\cdot b + _6C_2 a^4\cdot b^2 + _6C_3 a^3\cdot b^3 + _6C_4 a^2\cdot b^4 + _6C_5 a\cdot b^5 + b^6$ .

And if we let $a = b = 1$ we are left with the coefficient on the right side of the equation. That is we have:

$1^6 + _6C_1 1^5\cdot 1 + _6C_2 1^4\cdot 1^2 + _6C_3 1^3\cdot 1^3 + _6C_4 1^2\cdot 1^4 + _6C_5 1\cdot 1^5 + 1^6$

$=1 + _6C_1 + _6C_2 + _6C_3 + _6C_4 + _6C_5 + 1$

$= 1 + 6 +15 + 20 + 15 + 6 + 1 = 64$

Since we let $a = b = 1$ , the left side of the expansion $(a + b)^6$ becomes $(1 + 1)^6 = 2^6 = 64$

We can actually extend this.

For example, we wish to determine the sum of the coefficient of the binomial expansion $(a + b)^n$ , where $n \in N$ , then the coefficient can be computed by letting $a = b = 1$ . That is, the sum of the numerical coefficient will be $2^n$

We can still extend this. What if we have numerical coefficient in the binomial.

For example, what is the sum of the numerical coefficient of $(2a + 3b)^2?$

Since $(2a + 3b)^2 = (2a)^2 + 2(2a)(3b) + (3b)^2 = 4a^2 + 12ab + 9b^2$ . We can easily see that the sum of the coefficient is $4 + 12 + 9 = 25$ .

However, if we let $a = b = 1$ we get $(2 + 3)^2 = 5^2 = 25$ which is our answer.

Now let us try finding the sum of the coefficient of $(2a -3b)^4$ . You can check that the answer is 1 .