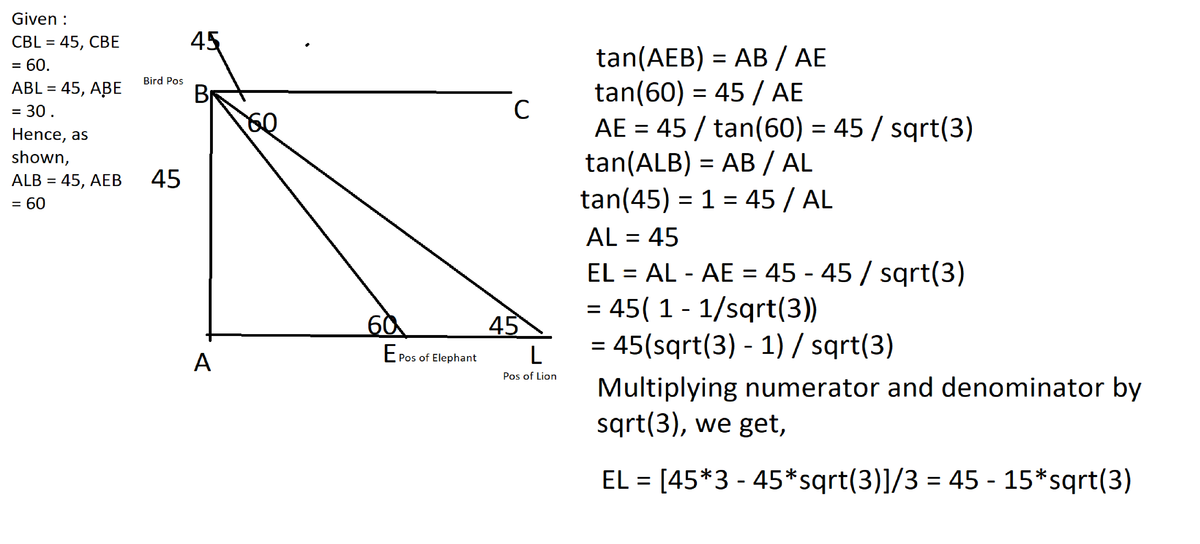
Bird's Eye View (Mathathon Problem 7)
A bird sitting on a tree noticed a lion following an elephant coming towards the tree.
The bird was 4 5 m above the ground. From her point of view, the angles of depression of the lion and the elephant were 4 5 ∘ and 6 0 ∘ respectively.
How far was the lion from the elephant in metres?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
First of all, let's give some names to the known values!
Let x e be the position of the elephant on the ground and let ϵ = 3 π be the elephant's angle of depression from the bird's eye view.
Let x l be the position of the lion on the ground and let λ = 4 π be the lion's angle of depression from the bird's eye view.
What we want to find is the distance d = x l − x e
Now we can make a drawing of the whole situation (not to scale).
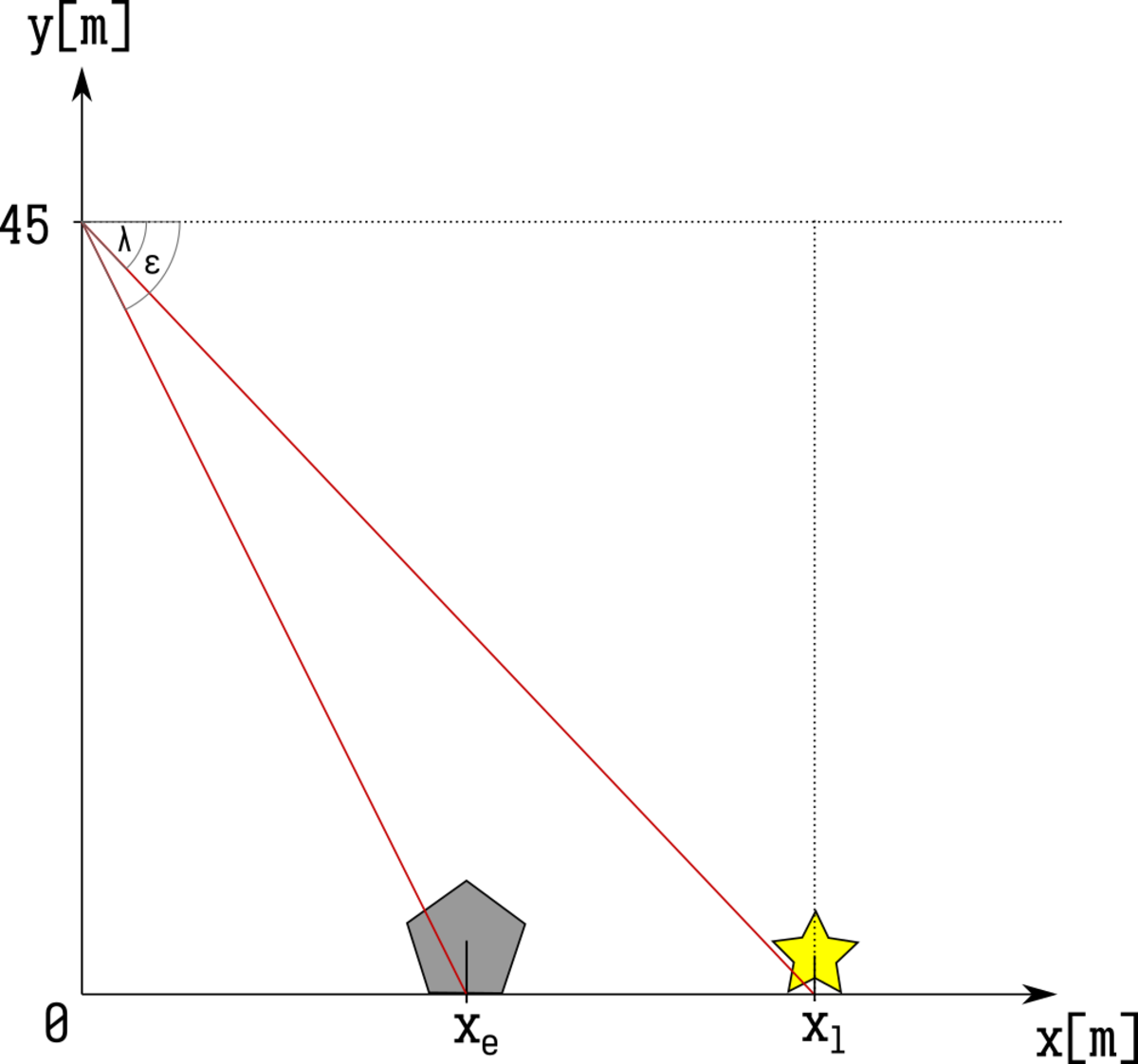
One nice thing immediately springs to attention. The diagonal of a square has angle 4 π with respect to the horizontal, just like our lion! Since the sides of a square have equal length and the bird's location is perpendicular to the ground, we can immediately conclude that x l must also equal 4 5 m .
Now we still need x e . It isn't too hard to see that the angle of depression of the elephant plus some angle must equal 2 π , let's call that angle ϵ , so that we get ϵ + ϵ = 2 π ⟺ ϵ = 2 π − ϵ . What's left is to note that we know the angle ϵ , the height of the bird and want to know the length of the other leg of the right triangle which the three are part of - this just begs for some trigonometry! So let's take the tangent of ϵ : tan ϵ = 4 5 x e ⟺ x e = 4 5 ⋅ tan ϵ That was already the hardest part, but further simplification can make the problem even easier. It can be proven that tan ϵ = tan [ 2 π − ϵ ] = cot ( ϵ ) = cot [ 3 π ] = 3 3 . All that's left to do is plugging in these values! d = x l − x e d d = 4 5 − x e = 4 5 − 3 4 5 ⋅ 3 = 4 5 − 1 5 3
a s i n ( A ) = b s i n ( B ) So, we start off with 4 5 s i n ( 6 0 ) = x s i n ( 9 0 ) We then cross multiply to get 4 5 ( s i n ( 9 0 ) ) = x ( s i n ( 6 0 ) ) 4 5 = x ( 0 . 8 6 6 0 2 5 4 0 3 7 8 ) So x = 5 1 . 9 6 1 . We then repeat the process to obtain 5 1 . 9 6 1 s i n ( 4 5 ) = y s i n ( 1 5 ) . We again cross-multiply to obtain 5 1 . 9 6 1 ( ( 6 − 2 )/ 4 ) = y\(\frac{1}{\sqrt{2} We finally obtain by rearranging , \frac{y}{\sqrt{2} to get y = 1 9 . 0 1 9 = 4 5 − 1 5 ( 3 )
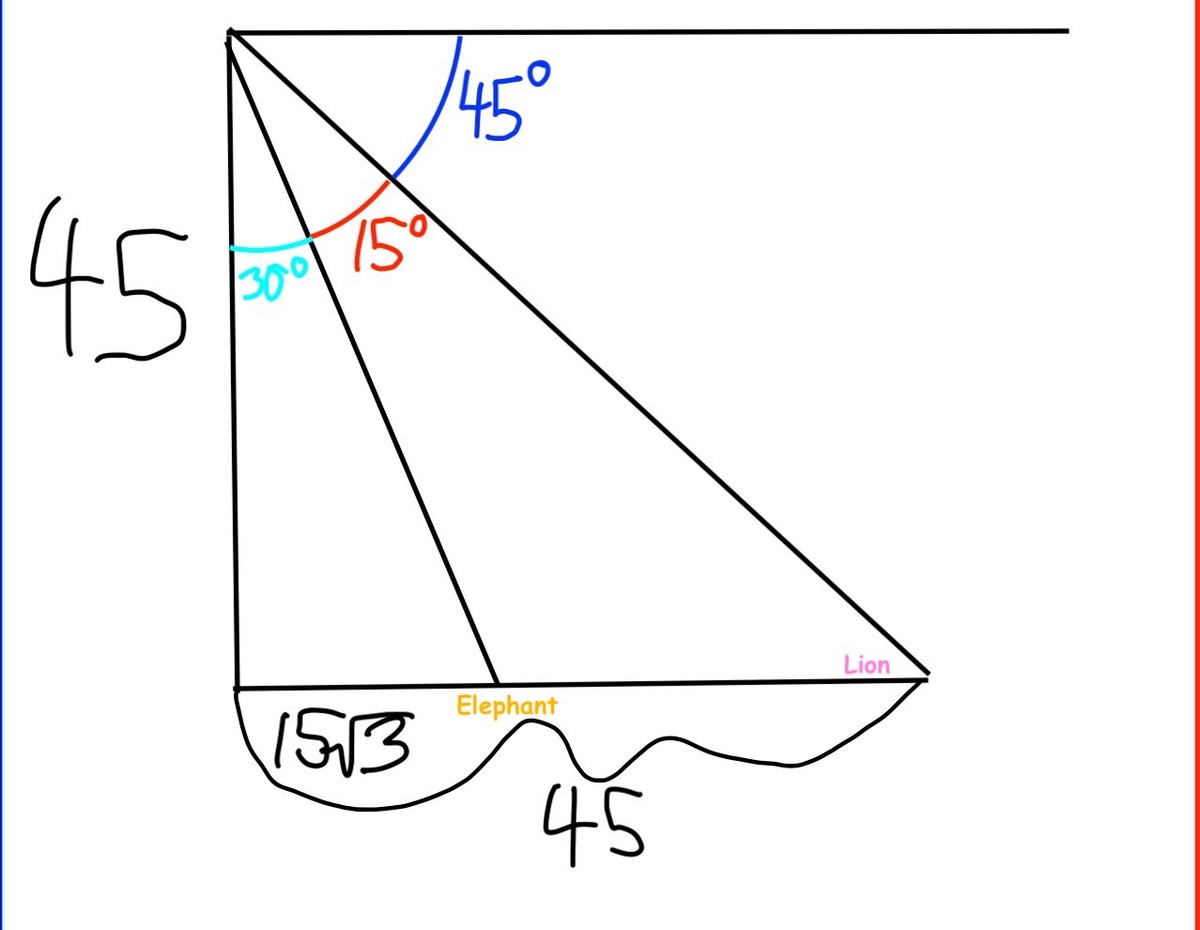
In the graph above, we can see that the triangle that the elephant is a vertex of is a 30-60-90 triangle. Since the 45 meter side is the long leg, the shorter leg of a 30-60-90 triangle is always the longer leg of the triangle × 3 ( 3 ) , so the shorter side of the 30-60-90 triangle, which is the distance from the bird to the elephant, is, in this case, 1 5 ( 3 ) . The bigger triangle is a 45-45-90 triangle, and because the leg lengths are always the same in a 45-45-90 triangle, the distance from the tree to the lion is 45 meters. Taking the difference between out two distances, we get 4 5 − 1 5 ( 3 ) , which is our final answer.
there's your red and blue lines I guess
and my handwriting reveal sry for "unrecognizable handwriting"-mom
 Bird witnessed a crime
Bird witnessed a crime
Let B 1 be the distance from tree to 🦁
And B 2 be the distance from tree to 🐘
t a n 4 5 ° = B 1 4 5
t a n 6 0 ° = B 2 4 5
t a n 4 5 ° =1
t a n 6 0 ° = 2 √ 3
Hence B 1 = 4 5 ∗ 1 and B 2 = √ 3 4 5
Note:we can rationalise √ 3 4 5 * √ 3 √ 3 to get 1 5 ∗ √ 3
To find the distance between the 🦁 and the 🐘: Subtract B 1 and B 2
Subtracting the two we get,
4 5 − 1 5 √ 3
Hence option B is correct!
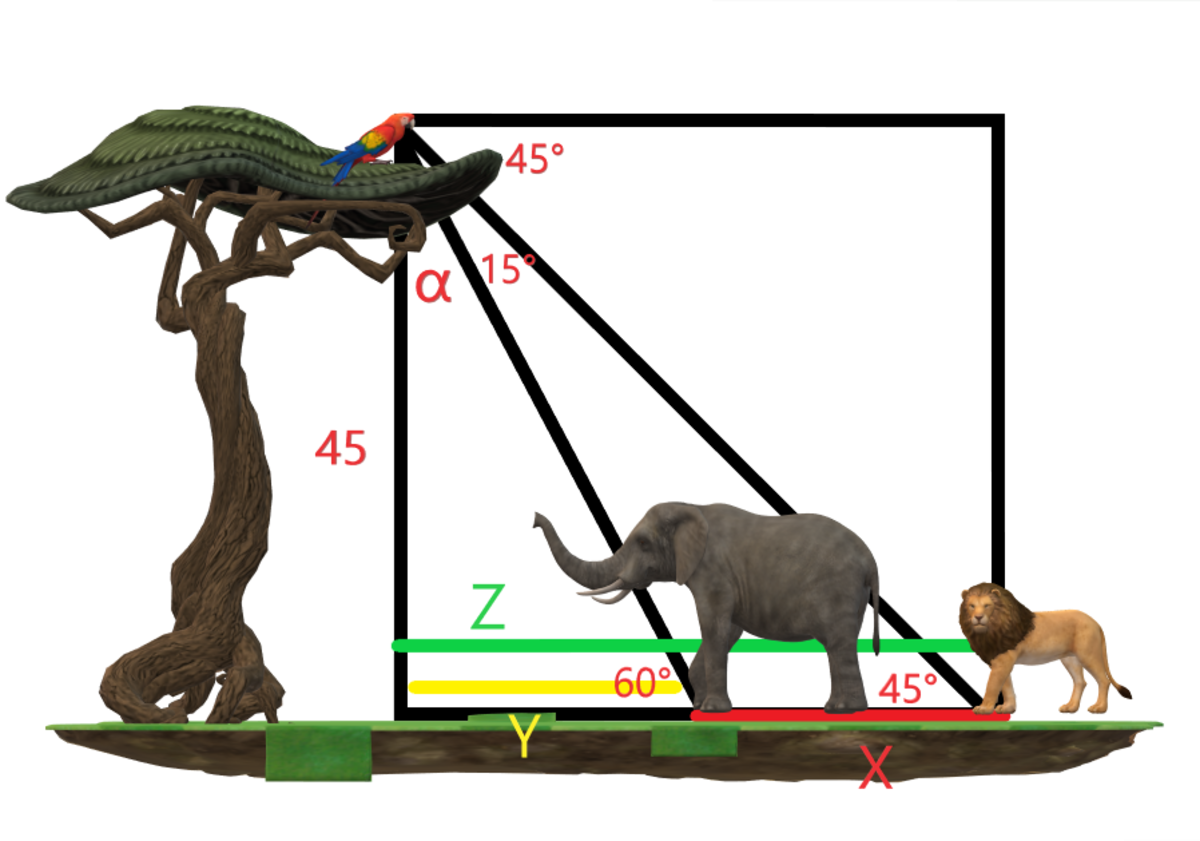
α = 3 0 ° ( 9 0 ° − 4 5 ° − 1 5 ° )
tan θ = Adjacent Opposite
Y = 4 5 tan α = 4 5 tan 30° = 4 5 ⋅ 3 1 = 3 1 5 ⋅ 3 = 1 5 3
Z = 4 5 tan ( α + 1 5 ° ) = 4 5 tan ( 3 0 ° + 1 5 ° ) = 4 5 tan 45° = 4 5 ⋅ 1 = 4 5
X = Z − Y = 4 5 − 1 5 3
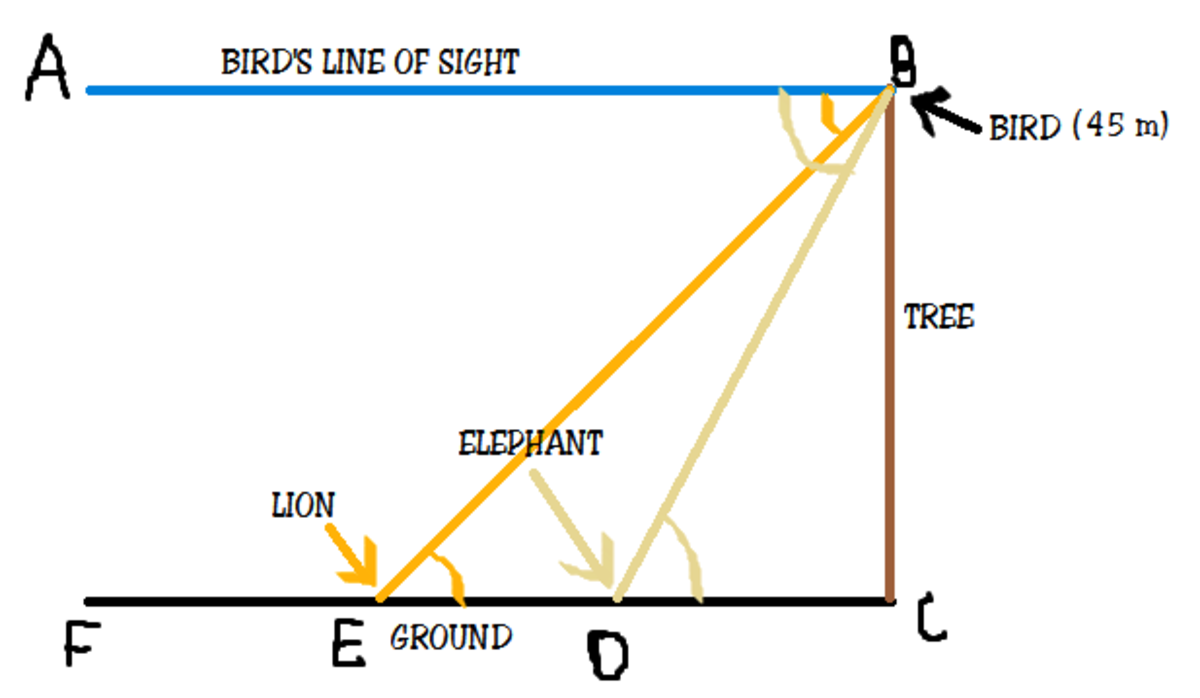 birds eye view
birds eye view
Look at the picture. It is given that ∠ A B E = 4 5 ° (the yellow angle) and ∠ A B D = 6 0 ° (the cinnamon angle)
From this we get ∠ B E C = 4 5 ° and ∠ B D C = 6 0 ° ∵ A B ∥ C F and they are alternate interior angles
We need to find E C − D C
BEC and BDC are two triangles right-angled at C and we know BC = 45m and also the measures of angles BEC and BDC.
We can use trigonometry for this. We will use t a n θ = h y p o t e n u s e o p p o s i t e to get EC and DC.
For △ B E C :
t a n 4 5 ° = E C B C
E C = t a n 4 5 ° B C
E C = 1 4 5 = 4 5 m
For △ B D C :
t a n 6 0 ° = D C B C
D C = t a n 6 0 ° B C
D C = 3 4 5 = 3 4 5 3 = 1 5 3 m
Now E C − D C = 4 5 m − 1 5 3 m
Therefore, the distance between the lion and the elephant = 4 5 m − 1 5 3 m
This is how I solved it. For the 45 degree angle, it creates an isosceles triangle. The leg along the ground is the same length as the vertical leg, so the lion is 45 meters away.
For the elephant, it is half of an equilateral right triangle, so the leg along the ground is exactly half of the straight line distance between the bird and the elephant. Let x be the distance to the elephant. Using the pythagorian theorem:
- 4 5 2 + x 2 = ( 2 x ) 2
- 4 5 2 + x 2 = 4 x 2
- 4 5 2 = 3 x 2
- x = 3 4 5
- The answer is 4 5 ( l i o n ) − 3 4 5
- 4 5 − 1 5 3
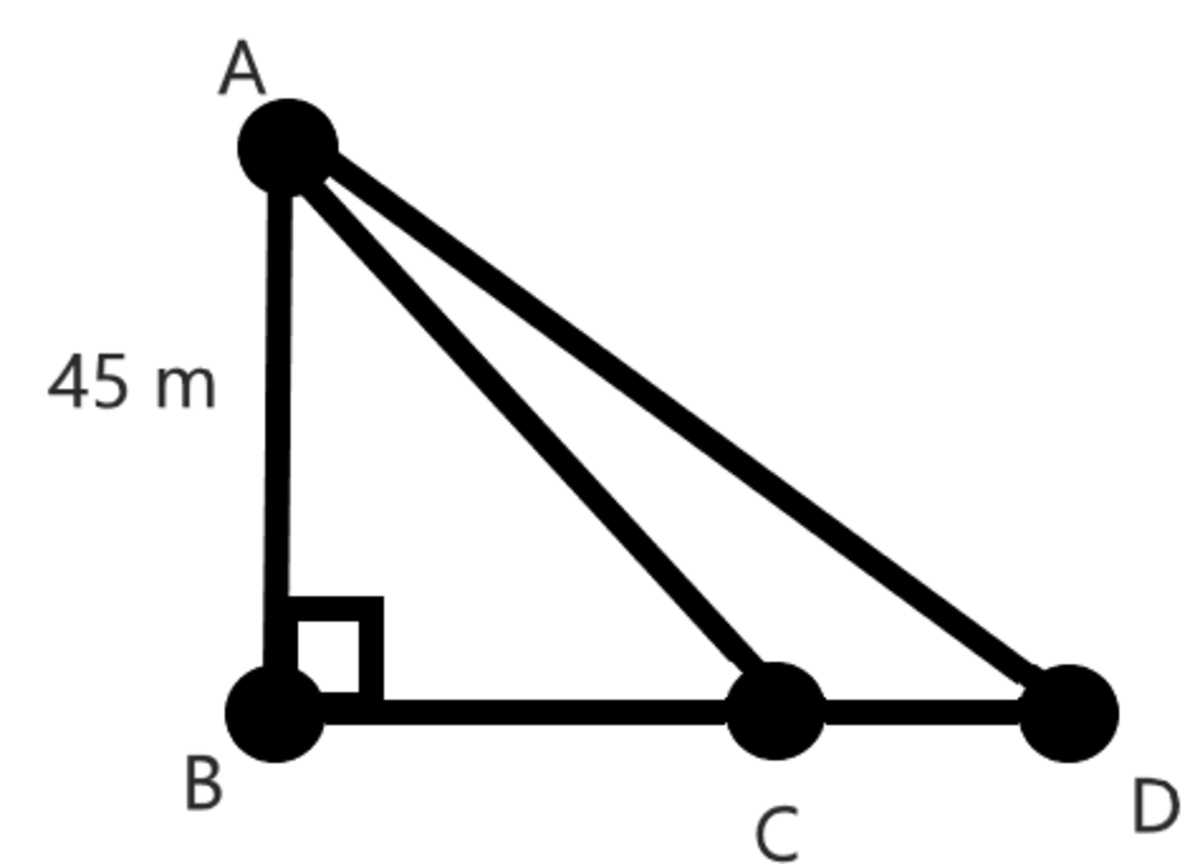 Picture
Since
a
n
g
l
e
B
A
C
=
a
n
g
l
e
A
C
B
=
4
5
∘
,
A
B
=
B
C
=
4
5
m
. We notice that
△
A
B
D
is a special
3
0
−
6
0
−
9
0
triangle, and the ratios of the sides of the triangle is
1
:
3
:
2
. Let
B
D
=
x
. According to the ratios of the sides of the triangle,
A
B
=
4
5
m
=
x
3
→
B
D
=
x
=
1
5
3
. Now that we already have the measurements, we can calculate the distance between the lion and the elephant, which is
4
5
−
1
5
3
Picture
Since
a
n
g
l
e
B
A
C
=
a
n
g
l
e
A
C
B
=
4
5
∘
,
A
B
=
B
C
=
4
5
m
. We notice that
△
A
B
D
is a special
3
0
−
6
0
−
9
0
triangle, and the ratios of the sides of the triangle is
1
:
3
:
2
. Let
B
D
=
x
. According to the ratios of the sides of the triangle,
A
B
=
4
5
m
=
x
3
→
B
D
=
x
=
1
5
3
. Now that we already have the measurements, we can calculate the distance between the lion and the elephant, which is
4
5
−
1
5
3
Log in to reply
@Brilliant Mathematics can you convert my comment to a solution? I accidentally pressed the wrong option.
Now we need to find DB - DC = BC
in Δ ABD, by using sin(45) = A B A D , we get
2 1 A B = A B A D = A D × 2 = 4 5 2 m
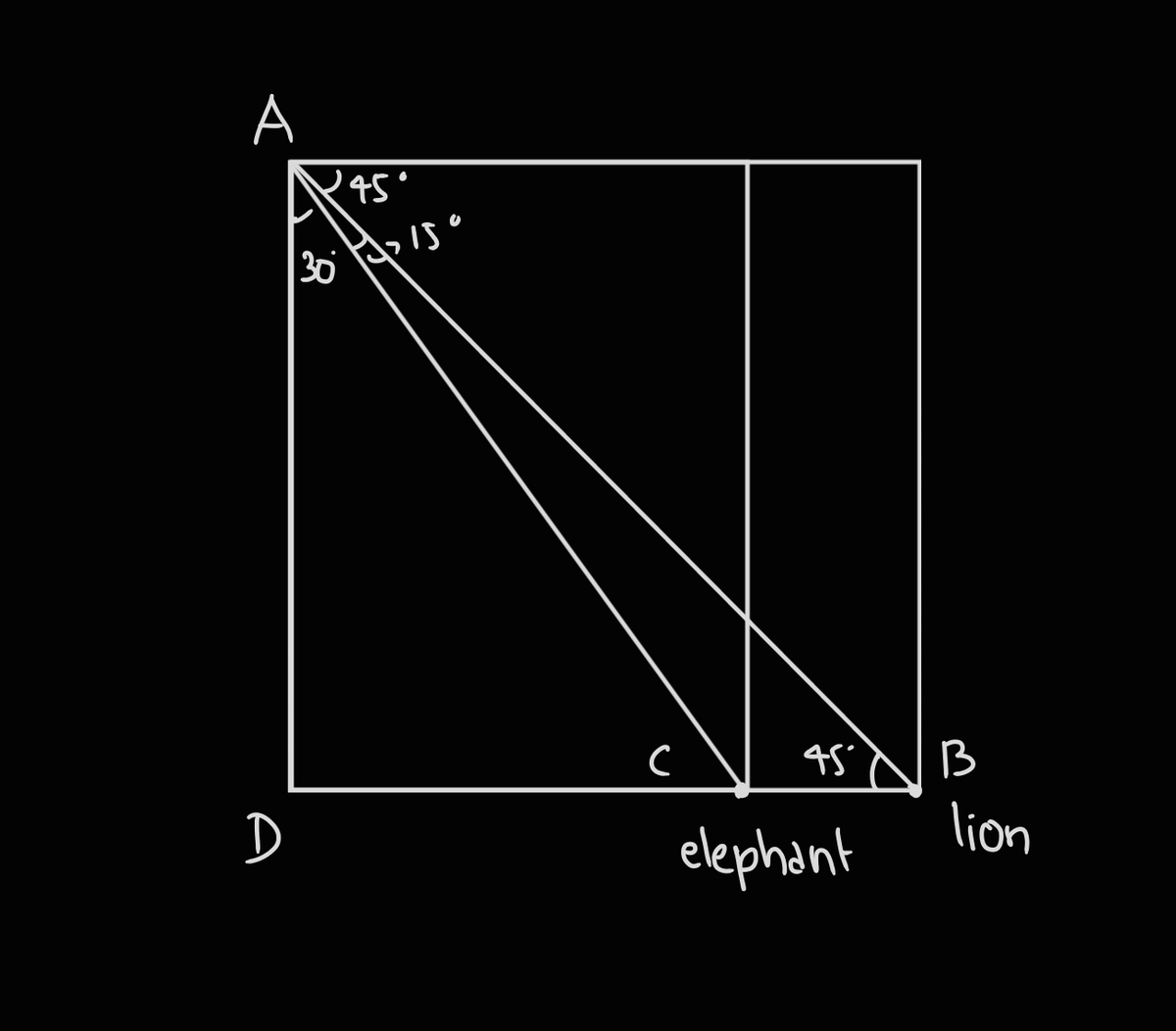 The above image indicates the positions of lion and elephant
The above image indicates the positions of lion and elephant
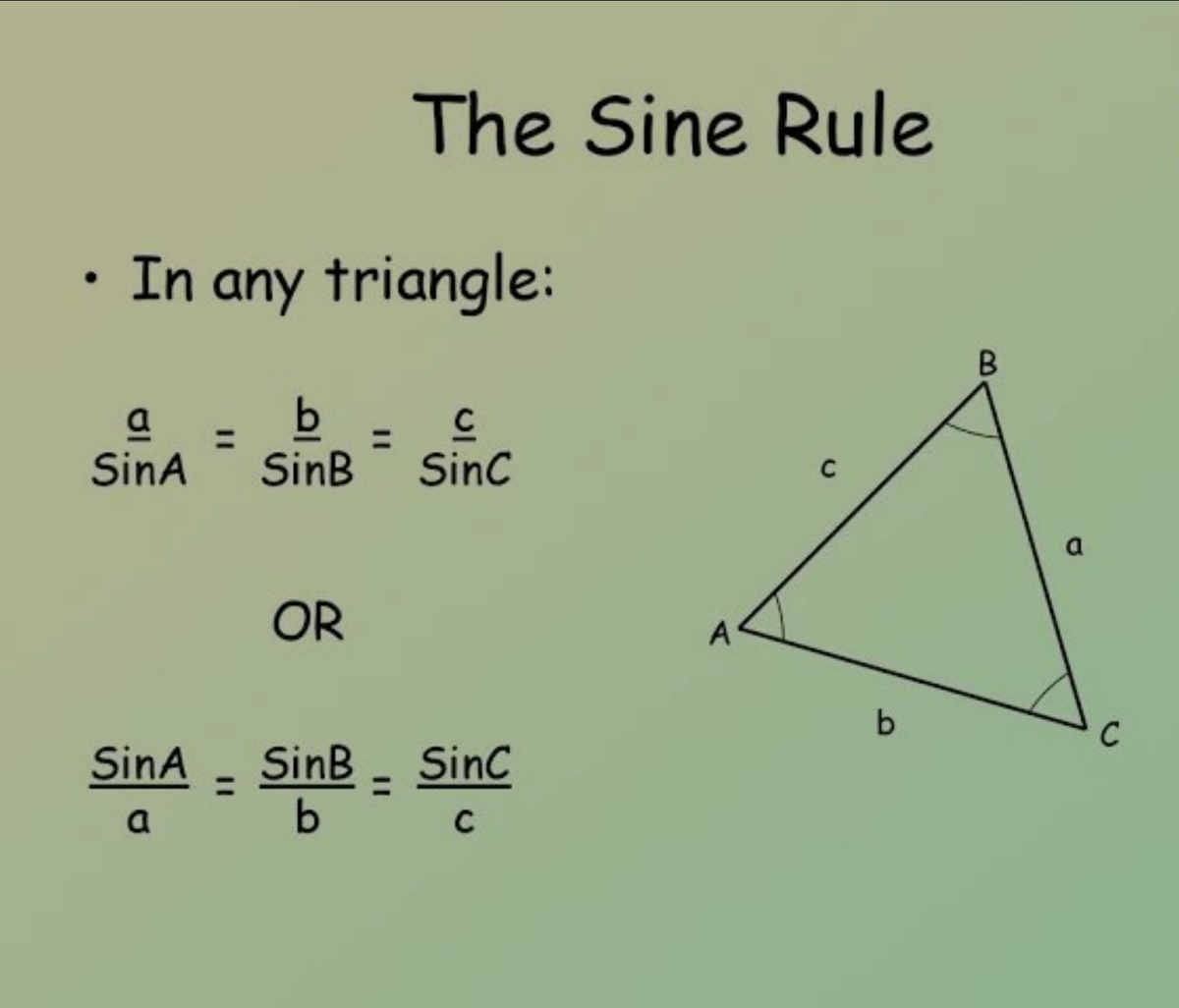
Now by applying sine rule in Δ ABC, we get
S i n ( 1 5 ) B C B C B C = S i n ( 1 2 0 ) A B = A B × S i n ( 1 2 0 ) S i n ( 1 5 ) = A B × S i n ( 6 0 ) S i n ( 1 5 ) ⇒ u s i n g S i n ( 1 8 0 − θ ) = S i n ( θ )
Now by substituting the values we get
B
C
=
4
5
2
×
2
3
2
2
3
−
1
=
4
5
3
3
−
1
=
4
5
−
1
5
3
Note:
- Sin(45) = 2 1
- Sin(15) = 2 2 3 − 1
- Sin(60) = 2 3
 The Sine Rule
The Sine Rule
What do you use for your images? I really like the style.
Log in to reply
I use Samsung notes
Log in to reply
Ok, cool :)
Log in to reply
@A Former Brilliant Member – Will you be posting more questions now or later, I am running out of questions
Log in to reply
@Omek K – 2 more questions today. After that I will score all solutions and then give results by april :)
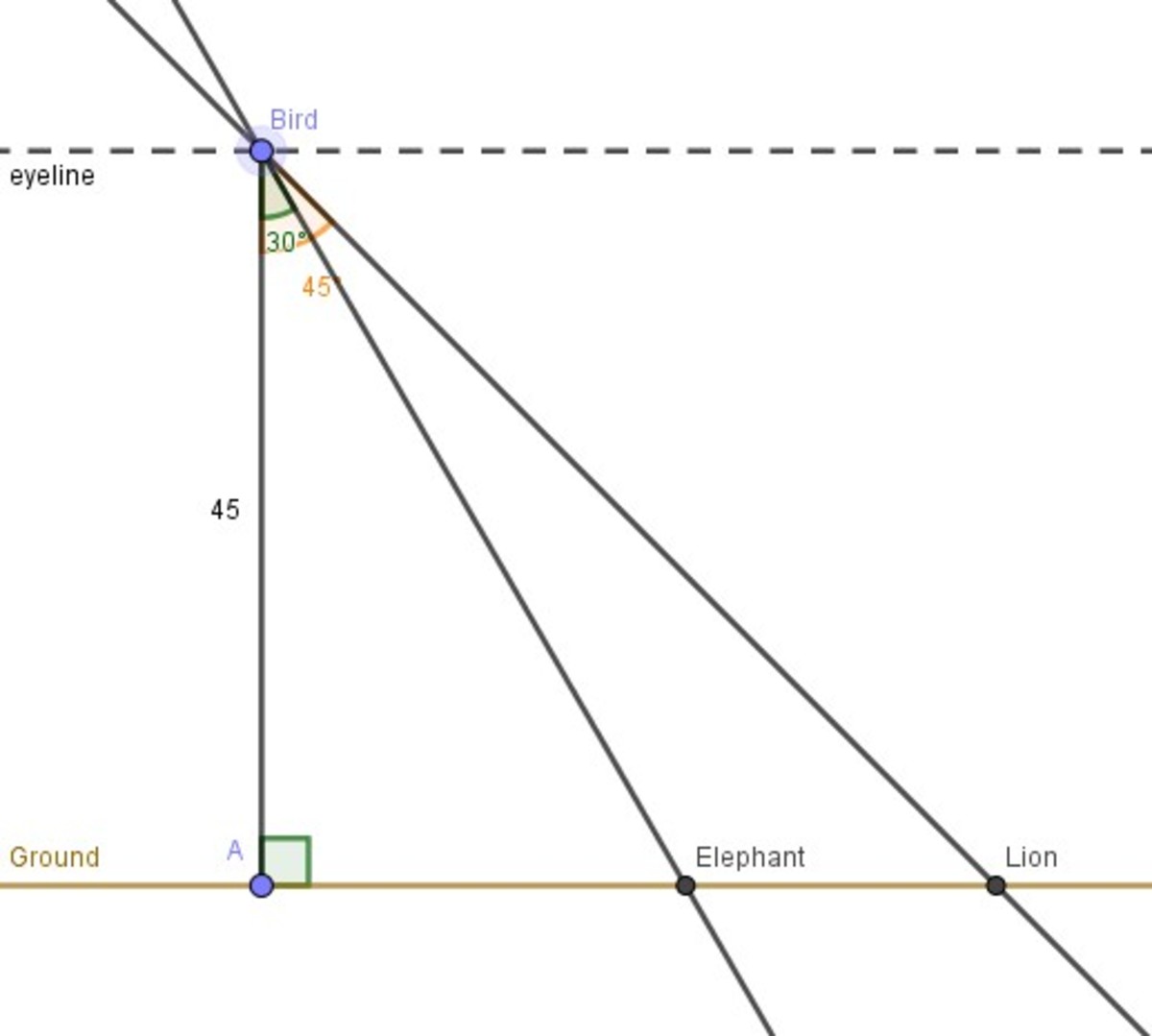
Let the Point where the bird is sitting be B, where the lion is be L, where the elephant is be E.
Simple calculations tell us that ∠ A B E = 3 0 ∘ & ∠ A B L = 4 5 ∘
In △ A B L , ∠ A B L = 4 5 ∘ & ∠ A = 9 0 ∘ . So ∠ A L B = 4 5 ∘ . Hence △ A B L is an isosceles triangle.
Hence , AL = AB = 45m
We have to find EL = AL - AE = 45 - AE. So EL is less than 45.
Now we can find the answer by eliminating the options (consider 3 = 1 . 7 )
Option 1 : 6 0 − 4 5 3 = 6 0 − 4 5 ⋅ 1 . 7 = − 1 6 . 5 As Distance can't be negative o p t i o n 1 i s e l i m i n a t e d .
Option 2 : 4 5 − 1 5 3 = 4 5 − 1 5 ⋅ 1 . 7 = 1 9 . 5 . Cannot be eliminated
Option 3 : 4 5 + 1 5 3 As d(EL) has to be less than d(AL) = 45 o p t i o n 3 i s e l i m i n a t e d .
Option 4 : 4 5 3 − 1 5 = 4 5 ∗ 1 . 7 − 1 5 = 6 1 . 5 o p t i o n 4 i s e l i m i n a t e d . (same reason as for option 3)
Only remaining Option 2 = 4 5 − 3 is the correct answer.
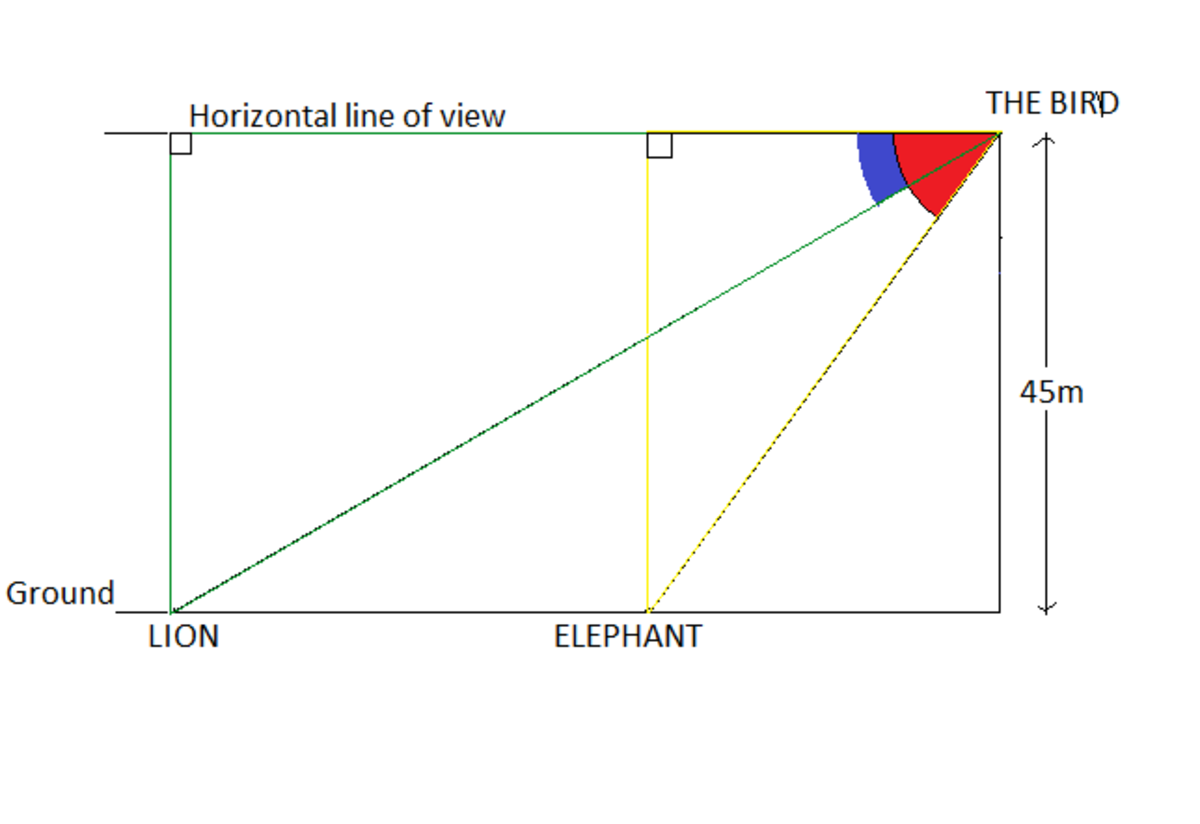
L e t t h e h o r i z o n t a l d i s t a n c e b e t w e e n t h e b i r d a n d t h e l i o n b e l a n d b e t w e e n t h e b i r d a n d t h e e l e p h a n t b e e i n y e l l o w △ tan 6 0 ° = e 4 5 m = 3 ⇒ e = 3 × 3 4 5 m × 3 = 3 4 5 3 m = 1 5 3 m i n g r e e n △ tan 4 5 ° = l 4 5 m = 1 ⇒ l = 4 5 m D i s t a n c e b e t w e e n t h e b i r d a n d t h e e l e p h a n t = l − e = ( 4 5 − 1 5 3 ) m
Using basics of trigonometry, 4 5 tan ( 4 5 ∘ ) − 4 5 tan ( 3 0 ∘ ) = 4 5 − 3 4 5 = 4 5 − 1 5 3
I don't want to draw lol
I misread the problem and tried to report, I deleted the report when I understood the question and now it shows I viewed the explanation for some reason?
Log in to reply
I think if you delete the report it shows like that, it has happened to me also once.
Log in to reply
it kinda makes sense because sometimes the unattended reports from others can contain the solution.... i don't know, just guessing
I think it is because if you report a problem, its answer is shown to you so that you can crosscheck your report. Did you click the wrong answer and then report, or report before giving an answer?
Log in to reply
@Percy Jackson I had a typo so I changed it, is it ok?
Log in to reply
@Vinayak Srivastava – Its fine Vinayak.
I reported it after reading the question, neither did I click an answer nor see an explanation beforehand, it showed I viewed the explanation after I deleted the report