Make a Perfect Square
2 1 2 4 + 2 1 2 6 + 2 n
Find the integer value of n such that the above expression is a perfect square.
The answer is 126.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Discussions for this problem are now closed
Happy birthday Vaibhav.
Your latex is not typed properly @Kalash Verma
Type the math terms b/w \( ...\)
Thanks Harsh.I just toggled the latex of the question and tried to do the same. My fault I did'nt learn it before trying.@Harsh
@A Former Brilliant Member – No worries!!
Now your sol n looks awesome, +1 for your solution!!
Thanks bhai
Happy birthday Vaibhav. Aaj mera bhi birthday hai!
@Kartik Bhardwaj – OH MY GOD !!!!!!!! Happy birthday to you too !!!!! :)
@Kartik Bhardwaj – Aur mera bhi. Belated happy birthday Vaibhav!!!:):):)
@Godwin Tom George – belated happy b'day to you too man !
@Vaibhav Prasad – @Vaibhav Prasad
@A Former Brilliant Member – Hey dude about your problem let's go back in time is it NcR or NpR
Maybe problem me mai 'closest to 126' ke jagah 'least value' bhi rakh sakta tha right ???
happy belated b'day.man!!...waise mujhe 14th August ko wish karna mat bhoolna..
DONE bhai !!!
@Vaibhav Prasad – chal phir.....yad rakhna bhai..
I think you meant to let x = n − 1 2 4 .
Yep! Thanks for corrections. I have edited the solution
Nice Solution!!
Since the said equation is a perfect square
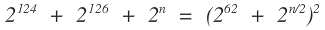
by binomial expansion
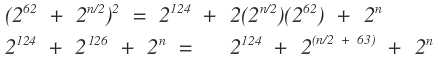
Then we can simply equate that
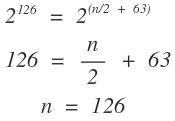
Best solution
Awesome solution!!
( a + b ) 2 = a 2 + b 2 + 2 a b - i
2 1 2 4 = ( 2 6 2 ) 2
2 1 2 6 = ( 2 ) ( 2 6 2 ) ( 2 2 n )
2 n = ( 2 2 n ) 2 - i i
Hence by comparing i i by i , we get n = 1 2 6
2 1 2 4 + 2 1 2 6 + 2 n
= 2 1 2 4 ( 1 + 4 + 2 x ). (Let n-124 be x)
We can see that 2 1 2 4 is a square number. So 1 + 4 + 2 x should also be square number.
So the least value of 2 x = 4
Hence x=2 and x=n-124 Therefore n=126