Bizarre cosines of gp!

$(1+\cos^2{20^\circ})(1+\cos^2{40^\circ})(1+\cos^2{80^\circ}) \\ = \left(1+\left[\dfrac{1+\cos{40^\circ}}{2}\right]\right)\left(1+\left[ \dfrac{ 1 + \cos{ 80^\circ}}{2}\right]\right)\left(1+\left(\dfrac{1+\cos{160^\circ}} {2} \right) \right) \\ = \dfrac{1}{8} (3 + \color{#3D99F6}{\cos{40^\circ}}) (3 + \color{#D61F06} {\cos{ 80 ^\circ}}) (3 + \color{#20A900} {\cos{ 160 ^\circ}}) \\ = \dfrac{1}{8} (3 + \color{#3D99F6}{a}) (3 + \color{#D61F06} {b}) (3 + \color{#20A900}{c}) \quad \quad [\text{Let } \color{#3D99F6}{a = \cos{40^\circ}}, \color{#D61F06} {b = \cos{ 80 ^\circ}}, \color{#20A900} {c = \cos{ 160 ^\circ}}] \\ = \dfrac{1}{8} [27 + 9(\color{#3D99F6}{a+b+c}) + 3(\color{#D61F06} {ab + bc + ca} ) + \color{#20A900} {abc}] \\ = \dfrac{1}{8} \left[27 + 9(\color{#3D99F6}{0}) + 3\left(\color{#D61F06} {-\frac{3}{4}} \right) + \left( \color{#20A900} {-\frac{1}{8}} \right) \right] \quad \quad [\text{See Note}] \\ = \dfrac{197}{64} \quad \quad \Rightarrow a + b = 197 + 64 = \boxed{261}$

$$

$\text{Note: }$ From the following identity:

$\begin{aligned} \cos{40^\circ} + \cos{80^\circ} \color{#3D99F6} {+ \cos{120^\circ}} + \cos{160^\circ} & = - \frac{1}{2} \\ \cos{40^\circ} + \cos{80^\circ} \color{#3D99F6}{- \frac{1}{2}} + \cos{160^\circ} & = - \frac{1}{2} \\ \Rightarrow \cos{40^\circ} + \cos{80^\circ} + \cos{160^\circ} & = 0 \quad \quad \color{#D61F06} {[ \text{Let } x = \cos{40^\circ} ]} \\ x + 2x^2 - 1 + 8x^4 - 8x^2 + 1 & = 0 \\ 8x^3 - 6x + 1 & = 0 \end{aligned}$

The roots to $8x^3 - 6x + 1 = 0$ are $\color{#3D99F6}{a = \cos{40^\circ}}$ , $\color{#D61F06} {b = \cos{ 80 ^\circ}}$ and $\color{#20A900} {c = \cos{ 160 ^\circ}}$

$\Rightarrow \begin{cases} \color{#3D99F6}{a+b+c = 0} \\ \color{#D61F06} {ab + bc + ca = - \frac{3}{4}} \\ \color{#20A900} {abc = - \frac{1}{8}}\end{cases}$

Start with $\cos^2(A) = \frac12 (\cos(2A) + 1)$ , then the trigonometric expression becomes

$\frac18 (3 + \cos(40^\circ))(3 + \cos(80^\circ))(3 + \cos(160^\circ ) )$

Note that $40 \times 3 =120, 80\times3=240, 160\times3=360 +120$ . Consider the triple angle formula $\cos(3x) = 4\cos^3(x) -3\cos(x) = -\frac12$ . Then $x = 40^\circ,80^\circ,160^\circ$ satisfy the previous equation. Let $y = \cos(x)$ , then $8y^3-6y + 1 = 0$ has roots $\cos(40^\circ), \cos(80^\circ),\cos(160^\circ)$ . Equivalently, $8(y-3)^3-6(y-3) + 1 = 0$ has roots $\cos(40^\circ) + 3, \cos(80^\circ) + 3,\cos(160^\circ) + 3$ .

Hence the Vieta's formula, the product in question is $\frac18 \cdot -\frac18 (-8\cdot3^3 +6\cdot3 + 1 ) = \boxed{\frac{197}{64}}$ .

Is there any shorter way, plz post yours

$\large{\cos ^{2}x=\frac{1+\cos 2x}{2}}$

The given expression becomes

Note that all angles are in degrees

$\large{\frac{1}{8}\color{#D61F06}{(3-\cos 20)(3+\cos 40)(3+\cos 80)}}$

As $\cos 160=-\cos 20$

on expanding

$\large{-9\cos 20+9\cos 40+9\cos 80 -\color{#20A900}{3\cos 20 \cos 40-3 \cos 20 \cos 80+3\cos 80 \cos 40}-\color{#3D99F6}{\cos20 \cos 40 \cos 80}}$

Now repeated use of some common properties

$\cos A+\cos B=2\cos(\frac{A+B}{2})\cos(\frac{A-B}{2})$

$\cos A-\cos B=2\sin(\frac{A+B}{2})\sin(\frac{B-A}{2})$

$2\cos A \cos B=\cos(A+B)+\cos(A-B)$

$4\cos(60-A)\cos (A) \cos(60+A)=\cos 3A$

$\sin 30=0.5$ and $\cos 120=-0.5$

$\sin A=\cos (90-A)$

Now we have

$\large{-9\cos 80+9\cos 80-\color{#20A900}{\frac{3}{2}((\cos 60+\cos 20)+(\cos100+\cos 60)-(\cos 120+\cos 40))}-\color{#3D99F6}{\frac{1}{4}\cos 60}+27}$

Collecting $\cos 60$ terms and reaaranging

$\large{(-\frac{9}{2}-\frac{1}{4})\cos 60+27+\frac{3}{2}(\cos 40-\cos 20-\cos 100)}$

$\large{\frac{197}{8}+\frac{3}{2}(\cos 40-2\cos 60 \cos 40)}$

=197/8

The final answer is

$\huge{\boxed{\frac{197}{64}}}$

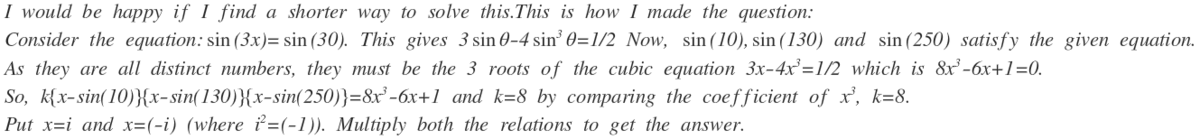I\quad would\quad be\quad happy\quad if\quad I\quad find\quad a\quad shorter\quad way\quad to\quad solve\quad this.This\quad is\quad how\quad I\quad made\quad the\quad question:\ Consider\quad the\quad equation:\sin (3x)=\sin (30).\quad This\quad gives\quad 3\sin \theta -4\sin ^{ 3 } \theta =1/2\quad Now,\quad \sin (10),\sin (130)\quad and\quad \sin (250)\quad satisfy\quad the\quad given\quad equation.\ As\quad they\quad are\quad all\quad distinct\quad numbers,\quad they\quad must\quad be\quad the\quad 3\quad roots\quad of\quad the\quad cubic\quad equation\quad 3x-4x^{ 3 }=1/2\quad which\quad is\quad 8x^{ 3 }-6x+1=0.\ So,\quad k{ x-sin(10)} { x-sin(130)} { x-sin(250)} =8x^{ 3 }-6x+1\quad and\quad k=8\quad by\quad comparing\quad the\quad coefficient\quad of\quad x^{ 3 },\quad k=8.\ Put\quad x=i\quad and\quad x=(-i)\quad (where\quad i^{ 2 }=(-1)).\quad Multiply\quad both\quad the\quad relations\quad to\quad get\quad the\quad answer.