Easy Hyperbolic Summation
S = n = 1 ∑ ∞ ( 2 n − 1 ) 2 n − 1 1 = 1 + 6 1 + 2 0 1 + 5 6 1 + ⋯
If S can be represented as A sinh − 1 ( B ) , where A and B are integers . Find 1 0 0 ( A + B ) .
Bonus : Find the partial sum of the series above.
The answer is 300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
did you remove the picture in the question?
Log in to reply
nope. i didnt. i would not have. i would just have renamed the title which sounds a bit racist.
How do you solve the bonus question?
Log in to reply
we consider the summation n = 1 ∑ k x 2 n − 2 = x 2 − 1 x 2 k − 1 and do the same as i did. I havent tried it out as calculations will get tedious.
Log in to reply
@Aareyan Manzoor – Hmmm... that's what I started with, but I can't get a closed form.
Log in to reply
@Pi Han Goh
–
i cant either. a search on wolfram alpha gives
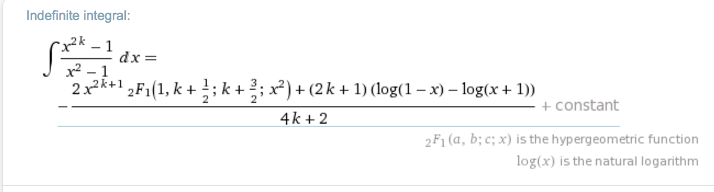
Log in to reply
@Aareyan Manzoor – There's one closed form by Lerch transcendent, but I doubt that's what the author had in mind.
Log in to reply
@Pi Han Goh – only if i knew this topic.. sorry i cant be of help here.
Log in to reply
@Aareyan Manzoor – Don't need to apologize. We're all learning =)
Log in to reply
@Pi Han Goh – Yes it is by lerch, my sister gave away this question.
look at the summation n = 1 ∑ ∞ x 2 n − 2 = 1 − x 2 1 integrating both side we have n = 1 ∑ ∞ 2 n − 1 x 2 n − 1 = 2 ln ( ∣ ∣ ∣ ∣ 1 − x 1 + x ∣ ∣ ∣ ∣ ) divide both sides with x and put x = 2 1 . n = 1 ∑ ∞ ( 2 n − 1 ) 2 n − 1 1 = 2 ln ⎝ ⎜ ⎜ ⎛ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 − 2 1 1 + 2 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ⎠ ⎟ ⎟ ⎞ = 2 2 ln ( 1 + 2 ) = 2 ln ( 1 + 2 ) we know a r c s i n h ( z ) = ln ( z + z 2 + 1 ) . at z =1, a r c s i n h ( 1 ) = ln ( 1 + 2 ) . so,the expression equals n = 1 ∑ ∞ ( 2 n − 1 ) 2 n − 1 1 = 2 a r c s i n h ( 1 ) and 1 0 0 ( 2 + 1 ) = 3 0 0