Blocks on table!
At a smooth horizontal table are two identical cubes of mass m , connected by a spring of rigidity k . The length of spring in the un-stretched state is l 0 . The right cube is linked to the load mass m at the end. At some time the system is released and the system moves without initial velocity. Find the maximum distance (in cm) between blocks during the motion of the system.
[ l 0 = 1 c m , m = 3 k g , k = 1 0 0 0 N / m ]
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good one , but please may you tell me , how Mg/3 came up .
Log in to reply
M = 2 m T = M a = 2 m a m g − T = m a ⇒ a = 3 g ⇒ T = M a = 3 M g = 3 2 m g
I think that's clear.
Is there any way to solve this question using reduced mass?
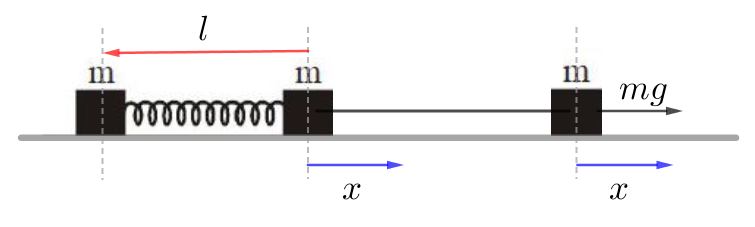 I defined the coordinates in the figure and applied Lagrangian mechanics:
I defined the coordinates in the figure and applied Lagrangian mechanics:
T = 2 1 2 m x ˙ 2 + 2 1 2 m ( x ˙ − l ˙ ) 2 kinetic energy V = 2 1 k ( l − l 0 ) 2 − m g x potencial energy
d t d ∂ l ˙ ∂ T = − ∂ l ∂ V ⟹ − m x ¨ + m l ¨ = − k ( l − l 0 ) m g ( 1 ) d t d ∂ x ˙ ∂ T = − ∂ x ∂ V ⟹ 3 m x ¨ − m l ¨ = m g − k ( l − l 0 ) ( 2 )
Combining ( 1 ) and ( 2 ) : l ¨ = − 2 m 3 k ( l − l 0 ) + 2 g ( 3 )
For the initial conditions l ( 0 ) = 0 and l ˙ ( 0 ) = 0 , the solution for ( 3 ) is: l ( t ) = A sin ( ω t − φ 0 ) + l 0 + 3 k m g , where ω = 2 m 3 k i φ 0 = arcsin ( 3 k A m g )
Given that l ˙ ( 0 ) = 0 , we can determine the value of A :
l ˙ ( t ) = ω A cos ( ω t − φ 0 ) l ˙ ( 0 ) = 0 ⟹ ω t − φ 0 = 2 π ⟹ A = 3 k m g ≈ 1 cm
The maximum value of l is reached when sin ( ω t − φ 0 ) = 1 :
l m a x = A + l 0 + 3 k m g = l 0 + 3 k 2 m g ≈ 3 cm
Appreciating the other solutions , here's my solution( others must also have done by this ) , just two steps .
Analyse the problem -
The elongation can be maximum only when the right block on the table stops .
F.B.D of the given block justifies that T =kx
now since right block stops , the load will also stop ( connected through string )
hence , T= mg
Equating , mg = kx , x = mg/k , x = 3*10 / 1000 m = 3 cm
Must be the easiest !!
Here, x is the elongation. Then how can we say that x is the maximum distance. The maximum length should be x + L .
Log in to reply
dude , Its asked during the motion .. .. did you like the solution ?
Log in to reply
I did! But how can you say that the distance between them will be the extension of the spring? If x is the distance, then k x = F s p r i n g .
Log in to reply
@Kishore S. Shenoy – See , the maximum dist. must be x+L . Now since the initial dist. was L . So x is the max. dist. b/w them "During Motion".
Shouldn't the block stop when its velocity is zero? when T=Mg it still has some K.E which will make it to move?
but, what if the maximum elongation when they all move with same speed ?
The question can be transformed to situation in which these blocks lie on the horizontal table and M g force acts on the right most block.
Let us consider these three blocks and spring as a system.
Net force acting on the system is M g . So the acceleration of the CoM of the system is g / 3 .
Let us choose our reference which is moving with CoM. As it is a non inertial frame so we have to consider pseudo force.
Now work done by all the external force on the system is equal to change in Kinetic and potential energy of the system. In order to have maximum separation change in KE should be zero.
As we have to find work done by external forces so we don't have to worry about tension in the string and force acting because of spring.
3 m g y − 3 m g x + ( m g − 3 m g x ) = 2 1 k ( x + y ) 2
On solving we get ( x + y ) = 2 c m . So Maximum distance between the blocks are 3cm.