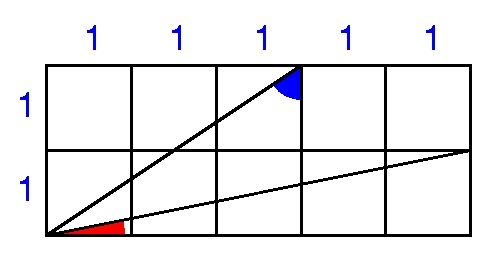
Blue and Red are in Half!
The rectangle above is divided into 10 squares.
What is (blue angle) − (red angle) in degrees?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
While it's a common technique to add lines to a geometric figure to aid in the solution, the grid for the original problem adds an extra barrier to realizing this. It's easy to get "locked in" and not realize the "graph paper" the problem uses can extend in any direction.
Great job. Thinking a little more, this construction shows the key fact is that the red triangle has legs of 3+2=5 and 3-2=1 (based on the blue triangle's legs of 3 and 2).
You could make similar problems/constructions to this one with sides x and y for the blue triangle and sides x+y and x-y for the red triangle.
Log in to reply
Right! I see where you're coming from, it's cool that we have the general case now. Maybe I should have included the red triangle with hypotenuse B C in the image.
Elegant solution without trigonometry.
Can you explain what motivated you to try this construction?
Log in to reply
Trig was instantly obvious, but much less exciting. I needed to find a way to represent the blue angle minus the red angle on the diagram, and extending B to C seemed to work- then it was just a matter of spotting things. It's been used in the above method too, but I thought the diagram in context would help too.
Wow. Your explanation doesn't exactly outline the rationale behind your statement, but your solution is awesome.
Log in to reply
Thanks, which part of the explanation is unclear?
Log in to reply
I think Barak-Har Elkin would find your explanation of the solution spot on if, as you discussed above with Matthew Feig, your diagram included the squares behind the triangle with hypotenuse BC, and you included the red angle there. Then the brilliance of the isosceles triangle ABC illuminating the subtraction of blue and red becomes visually evident. One final addition? a right angle indicator at the vertex of BAC. Then you hardly need words at all! :D
I thought inverse trig straight away. This is a beautiful solution!
Relevant wiki: Basic Trigonometric Functions
Let ∠ B be the blue angle and ∠ R be the red angle. Then ∠ B = tan − 1 ( 2 3 ) and ∠ R = tan − 1 ( 5 1 ) , and so
∠ B − ∠ R = tan − 1 ( 2 3 ) − tan − 1 ( 5 1 ) = tan − 1 ( 1 + 2 3 × 5 1 2 3 − 5 1 ) = tan − 1 ( 1 0 1 3 1 0 1 3 ) = tan − 1 ( 1 ) = 4 5 ∘ .
Smooth application of trigonometry. For someone without the knowledge of trig, this problem seems quiet hard (although not impossible)
Plz explain how tan inverse method use in
Log in to reply
Starting with the familiar formula
tan ( a − b ) = 1 + tan ( a ) tan ( b ) tan ( a ) − tan ( b ) ,
we then have that a − b = arctan ( 1 + tan ( a ) tan ( b ) tan ( a ) − tan ( b ) ) .
Then letting a = arctan ( A ) , b = arctan ( B ) we end up with
arctan ( A ) − arctan ( B ) = arctan ( 1 + A B A − B ) .
There are some restrictions on when the formula can be used but this is the general idea.
The same way man! (+1)
That isn't correct tangent is rise over run in that solution it is showing run over rise with the 3/2 and ride over run with the 1/5
Log in to reply
Tangent is better thought of as Opposite over Adjacent than rise over run. You will be able to see the correct sides to use more easily if you use that definition rather than the definition for slope. The rise over run only applies if a side touching the angle is on the x-axis.
How do you know that ∠ B A D = 9 0 ∘ ?
Log in to reply
<DAE = <ABF , <BAF + <ABF = 90 deg.
<BAD = <BAF + <DAE = <BAF + ABF = 90 deg.
The blue angle can be represented as the argument of the complex number 2+3i, and likewise the red angle as the argument of 5+i. Their difference would be the argument of (2+3i)/(5+i) = (13+13i)/26, which is 45 degrees.
Ah, solving this problem via complex numbers. An underrated approach! This brings me back to my high school years when I proved many Machin-like formula using this very method.
Good read!
Good solution hahahaah cool
 Let the
b
l
u
e
a
n
g
l
e
be
θ
, and the
r
e
d
a
n
g
l
e
be
ϕ
. Assuming the the side length of each square is
1
unit, we have
Let the
b
l
u
e
a
n
g
l
e
be
θ
, and the
r
e
d
a
n
g
l
e
be
ϕ
. Assuming the the side length of each square is
1
unit, we have
t a n θ = 2 3 ⟹ θ = 5 6 . 3 0 9 9 3 2 4 7
t a n ϕ = 5 1 ⟹ ϕ = 1 1 . 3 0 9 9 3 2 4 7
Finally,
θ − ϕ = 5 6 . 3 0 9 9 3 2 4 7 − 1 1 . 3 0 9 9 3 2 4 7 = 4 5
This method only shows that θ − ϕ is approximately equal to 45. The first 8 decimal places of θ and ϕ are the same, but it is possible that they may have different values further on.
This is quite similar to first problem of this week's intermediate set, where the two numbers have the same three digits after the decimal point but are not equal to each other.
tan(blue) = 3/2
tan(red) = 1/5
blue = arctan(3/2) = 56.3 degrees
red = arctan(0.2) = 11.3 degrees
blue-red = 45 degrees
This method only shows that (blue - red) is approximately equal to 45. The first decimal place of blue and red are the same, but it is possible that they may have different values further on.
This is quite similar to first problem of this week's intermediate set, where the two numbers have the same three digits after the decimal point but are not equal to each other.
Log in to reply
The problem only accepted integer solutions
Log in to reply
That doesn't mean that the answer has to be an integer. It is the responsibility of the solution writer to prove that the answer is exactly 45. This solution only says that "The answer is 45 because well, I can't submit a non-integer answer."
Log in to reply
@Pi Han Goh – The calculation shows that the answer is approximately 45, the problem only needed an approximate solution. As asked and answered, this calculation is sufficient to solve the problem.
Log in to reply
@A Former Brilliant Member – The question asked to find the exact solution, not "round your answer to the nearest integer" solution.
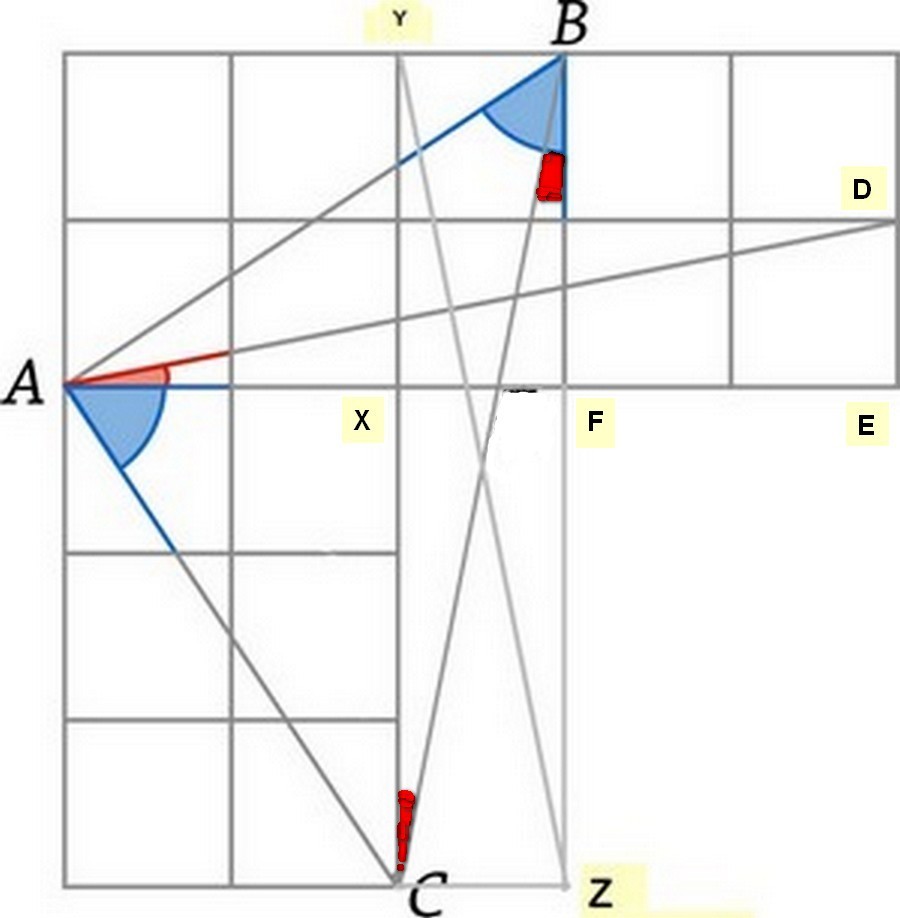
angle YCB = ZBC = DAE (red) (triangles CYB, ZBC, AED congruent)
angle ACX = BAF = (90 - ABF) = (90 - blue) (sum of angles in triangle BAF = 180)
AC = AB (triangles AXC, BFA congruent)
Therefore angle ACB = ABC (isosceles triangle ABC); ACX + YCB = ABF - CBF; (90 - blue + red) = (blue - red)
Thus, 2(blue - red) = 90 and (blue - red) = 45 degrees.
Oh, a nice variation of Dan Ley's approach! This certainly works too~
Tan b= 3/2 Tan r= 1/5 Tan(b-r)=(tan b-tan r)/1+(tan b)(tan r) ={(3/2)-(1/5)}/{1+(3/10)} =1 So, b-r=45° b is blue and r is red
For completeness, can you explain why tan ( b − r ) = 1 implies b − r = 4 5 ∘ only? Why can't b − r = 2 2 5 ∘ ?
It is 45 degrees.
Lets find tg(blue-red):
tg(b-r)=(tg(b)-tg(r))/(1+tg(b)
tg(r);
tg(b)=3/2; tg(r)=1/5
(1,5-0.2)/(1+1.5
0.2) = 1.3/1.3 = 1.
If tg(b-r)=1 then b-r=45 degrees.
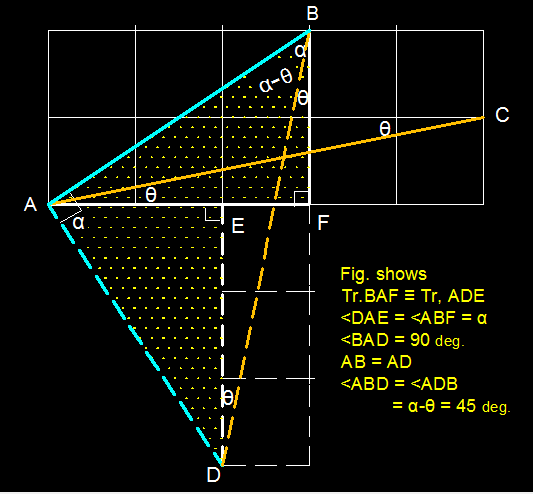
Since lengths A B = A C , △ A B C is right-angled and isosceles, so its other two angles are both 4 5
So, (blue angle) − (red angle) = ∠ A B C = 4 5