Blue-green trilemma

Geometry Level 2

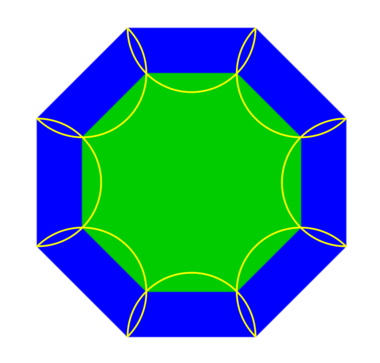Eight semicircles are drawn inside a regular octagon, each one having a side of the octagon as its diameter. Eight of their intersection points are the vertices of a new octagon. Which area is larger, blue or green?

Blue Green They are both equal

3 solutions

David Vreken
Jun 7, 2021

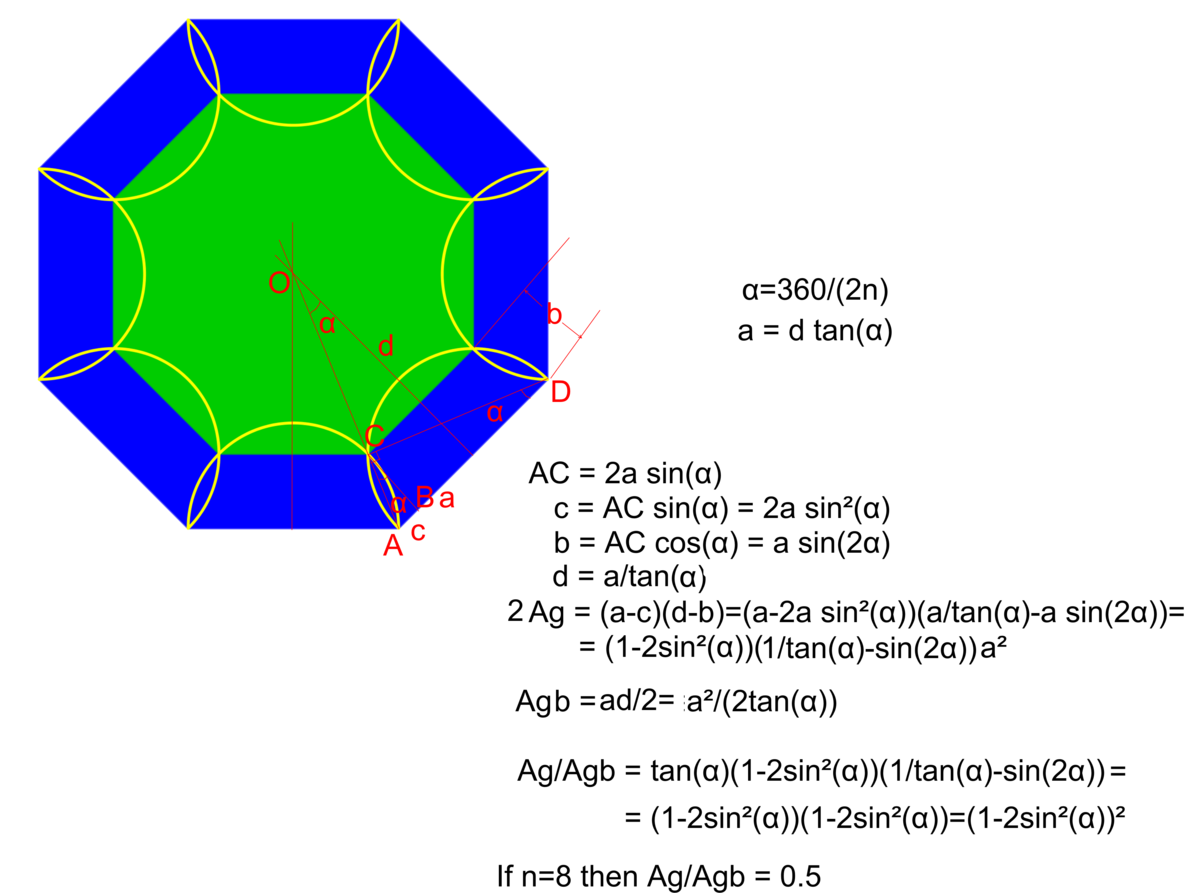
Partition the diagram as follows, where the sides of each rhombus and the legs of each right isosceles triangle are the same as the radii of each semicircle:

Since the blue and green regions are both made up of $8$ congruent rhombi and $8$ congruent triangles, their areas are equal .

Nice solution David! Thanks for posting. Let's enjoy the opportunity to communicate through Brilliant's Community as long as we still have it (unfortunately, not for much longer). And then, what?

Thanos Petropoulos - 5 days, 3 hours ago

Thanks!

I'm keeping an eye on this discussion: https://brilliant.org/discussions/thread/brilliant-community/

There's been talk about starting something on AoPS or trying to get a university to maintain the Brilliant community pages, so hopefully one of those options will work out.

David Vreken - 5 days, 1 hour ago

Yes, I am working on getting.... Hope that you two can join me if I do get through.

Chew-Seong Cheong - 4 days, 17 hours ago

@Chew-Seong Cheong – This is good news! If there is anything I can, do just send a note. Should we subscribe on AoPS in the meantime? Is there any other option? Is there a way we can communicate outside Brilliant?

Thanos Petropoulos - 4 days, 13 hours ago

@Thanos Petropoulos – Yes, subscribe to AoPS. I may not succeed in getting a host. My facebook account is https://www.facebook.com/chewseong.cheong/ and my email is cheongcs@gmail.com

Chew-Seong Cheong - 4 days, 13 hours ago

@Chew-Seong Cheong – Definitely! Thanks for doing that!

David Vreken - 4 days, 9 hours ago

Saya Suka
Jun 6, 2021

If we connect each of the green octagonal vertices to two of the nearest midpoint of edges of the outer blue octagon (the centers of the nearest semicircles), then clearly the length of the lines would be r (completely inside the semicircles), the same as the two opposite (and parallel) lines on two halves of the blue octagonal sides. This makes 8 rhombic shapes of sides r between the blue-green octagonal vertices with 45° as their acute angles. Two of them per blue outer sides takes up 2 × 45° = 90° of the semicircles', so green octagonal sides must be the hypothenuse taking up the other 90° half.

Green's side = √(r² + r²) = √2r
Blue's side = r + r = 2r

Green area : Blue area
= (√2r)² : (2r)² – (√2r)²
= 2r² : 4r² – 2r²
= 2r² : 2r²
= 1 : 1

Lu Ca
Jun 9, 2021

Blue-green trilemma

3 solutions

0 pending reports