Bonus Problem #2
x 2 x 2 = 1
How many integers of x satisfy the equation above?
Note: 0 0 is undefined.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Moderator note:
There's a simpler approach.
Hint : x 2 x 2 = ( x 2 ) x 2 .
Nice solution sir. But is there any way to prove that these are the only two solutions?
Log in to reply
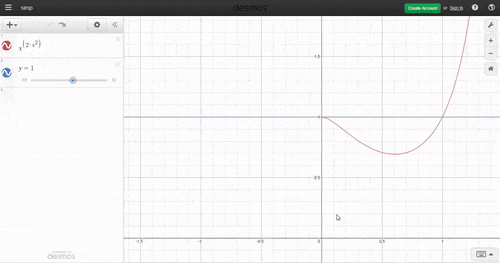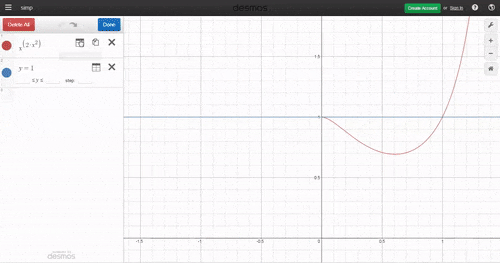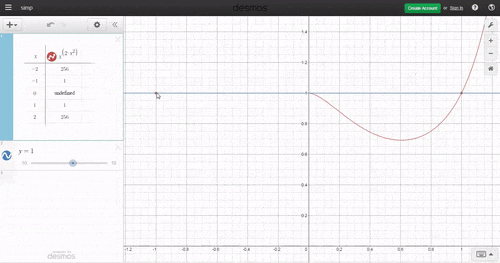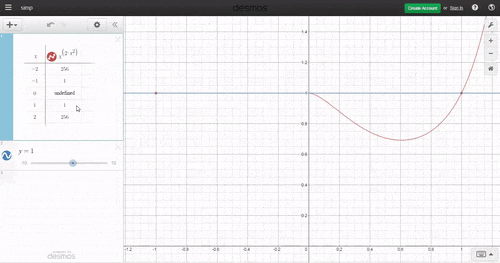
u can check it out by drawing the graph of y = x 2 x 2 and y = 1 , they both intersect at two integer points 0 and 1
check it out over here
Log in to reply
What about x = − 1
Why doesn't the graph show negative values of x? (Just want to know)
It could be argued that there could be 3 values. -1, 1 and 0.
Here are some sources that suggest that there are some ways that 0^0 = 1
https://www.math.hmc.edu/funfacts/ffiles/10005.3-5.shtml http://mathforum.org/dr.math/faq/faq.0.to.0.power.html http://www.askamathematician.com/2010/12/q-what-does-00-zero-raised-to-the-zeroth-power-equal-why-do-mathematicians-and-high-school-teachers-disagree/
Log in to reply
Officially, 0 0 is undefined.
Log in to reply
You're no fun. Didn't you read any of the links I provided?
Log in to reply
@Norm Nolasco – There is a reason for why the value of 0 0 is undefined.
We know that x 0 = 1 but we also know that is 0 x = 0
From the above points we have two values for 0 0 - 1 and 0. So the value of 0 0 remains undefined.
PS : There might be more ways to prove 0 0 is undefined.But this is the method that i know.
Log in to reply
@Athiyaman Nallathambi – Algebraically, perhaps it should be 1. Using the "official" definition, a x : = e l n x , but ln 0 is undefined.
@Athiyaman Nallathambi – Yes, it "should" be 1, but the official ruling is that it isn't anything at all. In a way it makes little practical difference, anyway.
That's exactly what I thought, but then since it was deemed incorrect, I suggested 2 values, excluding 0^0 .
Why only 1, -1
Note x 2 x 2 = ( x 2 ) x 2 = 1 1 so x 2 = 1 ⇒ x = ± 1 .
Sravanth Chebrolu Proof that the cases are the few ones mentioned in the solution:
Let 0 < a = 1 be another answer (by false assumption).Then we'd have:
a 2 a 2 = 1 → ( 2 a 2 ) l o g a = l o g 1 → ( 2 a 2 ) l o g a = 0
→ 2 a 2 = 0 ∨ l o g a = 0 → a = 0 ∨ a = 1
Which is indeed a contradiction that proves that ∀ a ≥ 0 ↔ a = 0 ∨ a = 1
Also for x < − 1 we'll prove that the equation cannot hold:
x < − 1 → x 2 > 1 → ( x 2 ) x 2 > 1 x 2 = 1 → x 2 x 2 > 1
And hence we're done.
By the way,how are you feeling?Are thing starting to get better?
Well done sir! and yes I'm a lot better now, but it's my father who is still down . . .
Log in to reply
Hope he gets better soon.And please don't call me sir xD, we merely have 2 years in difference!. Call me Arian if you wish.
Well if x 2 x 2 = 1 i f x = 1 , 1 2 = 1 Considering the exponent is two multiplied by a number, and the answer is one, we can assume that the exponent cannot be higher than one. However, we can still test for negative one. x 2 x 2 = 1 , i f x = ( − 1 ) , x 2 x 2 = − 1 2 = 1
0^0 is not undefined. It is 1. The "correct" answer is two, with x being equal to either 0 or 1, but there could also be three solutions, with x being equal to -1.
Similarly we can just simplify it to
x^{2x^{2}} - 1 = 0
And just following through with that and expanding, we have
(x^{x^{2}} + 1) (x^{x^{2}} - 1)
Giving 2 solutions of 1, -1
(xᵡ² + 1)(xᵡ² ̶ 1) = 0 .... maybe that's enough... I hope.
x 2 x 2 = ( x 2 ) x 2 = 1 = 1 1 so x 2 = 1 x = 1 , o r x = − 1 So, they have t w o value
1 and -1 because (-1)^2(-1)^2=1 and also anything power 1 is 1 itself.
Note that if $|x|>1$ , $x^2>1$ and this way, $(x^2)^{x^2}>1$. So, $|x|=1$ because $x$ is a integer number.
Case 1: 1^2*1²=1
Case 2: -1^2*(-1)²=1
0^0 is undefined.
x^(2x^2)=1 or, log(x^(2x^2))=log1 or, (2x^2)logx=0 [as, log1=0] eighther, (2x^2)=0 or, logx=0 or, x=0 or x=1 that means x has two values
There are in fact 2 solutions:
-1,1 are all integers and solve the equation as one can easily verify.
Note: 0 0 is often considered indeterminate.
Case 1: 2 x 2 = 0
⇒ x = 0 but if x = 0 ⇒ x 2 x 2 = 0 2 ∗ 0 2 = 1
Case 2: x = 1
⇒ x 2 x 2 = 1 2 ∗ 1 2 = 1
Case 3: x = − 1 for even exponent
⇒ x 2 x 2 = ( − 1 ) 2 ∗ ( − 1 ) 2 = 1
So, they have two value.