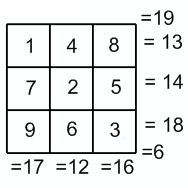Boring Square

Algebra Level 2

Is it possible to fill a $3 \times 3$ grid with integers $1,2,3,...,9$ such that the sum of the integers is unique in every row, column and diagonal ?

No Yes

3 solutions

Munem Shahriar
Dec 15, 2017

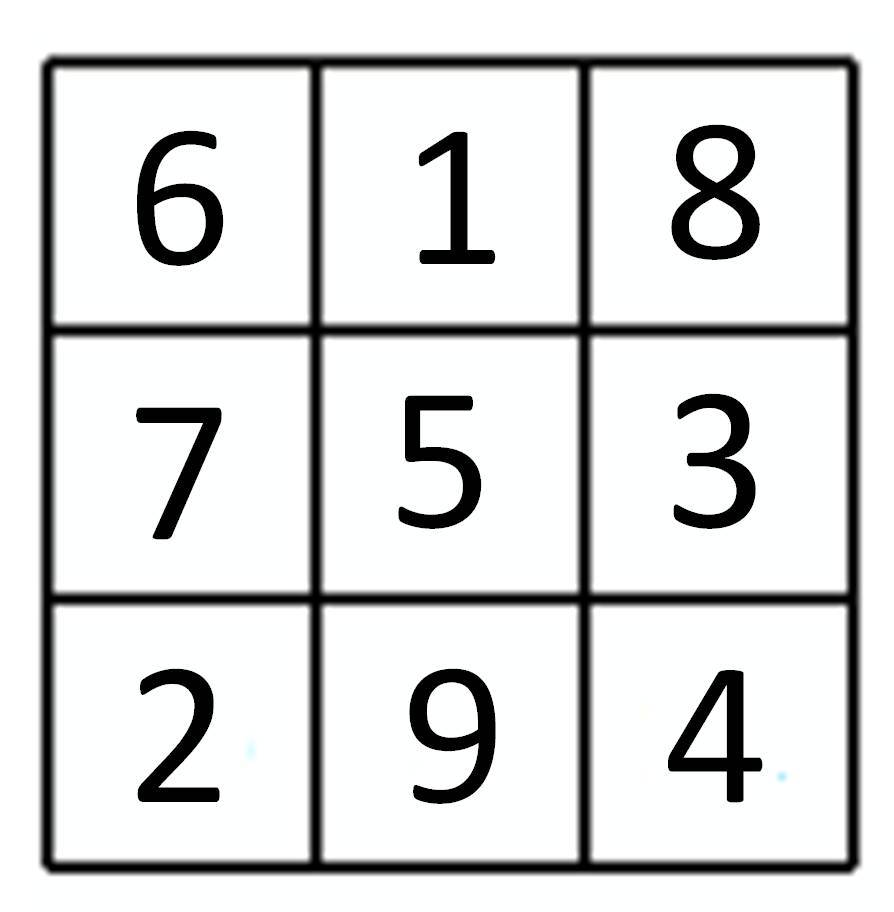
@Munem Sahariar How many configuarations are there?

Sumukh Bansal - 3 years, 5 months ago

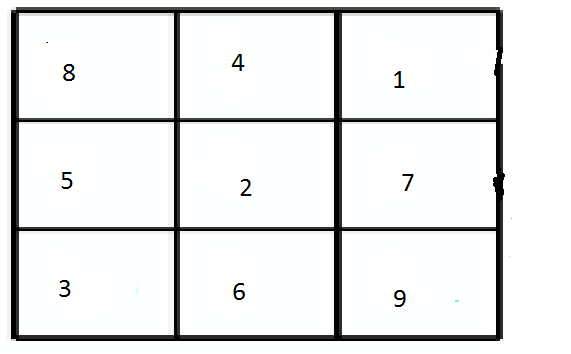
I found $3120$ different configurations ( $24960$ if we count reflections and rotations as different configurations.)

Romain Bouchard - 3 years, 5 months ago

How did you arrive at this conclusion?

Sumukh Bansal - 3 years, 5 months ago

@Sumukh Bansal – Brute force : I just listed all permutations of $123456789$ and kept only those for which all rows, columns and diagonals are different. I did not figure out a clever way to count but if so I might post a problem on it.

Romain Bouchard - 3 years, 5 months ago

@Romain Bouchard – Please elaborate!

Sumukh Bansal - 3 years, 5 months ago

@Sumukh Bansal – I think he wrote a code, that checks if a certain configuration meet the requirements of the problem.

Bar Kam - 3 years, 2 months ago

Romain Bouchard
Dec 15, 2017

Here is one solution :

How did you find such a configuration? How many other configurations are there?

Pi Han Goh - 3 years, 5 months ago

By error and trial :) After a little research, I found $3120$ different configurations ( $24960$ if we count reflections and rotations as different configurations.)

Romain Bouchard - 3 years, 5 months ago

A Former Brilliant Member
Dec 29, 2017

Boring Square

3 solutions

0 pending reports