Bouncing Higher
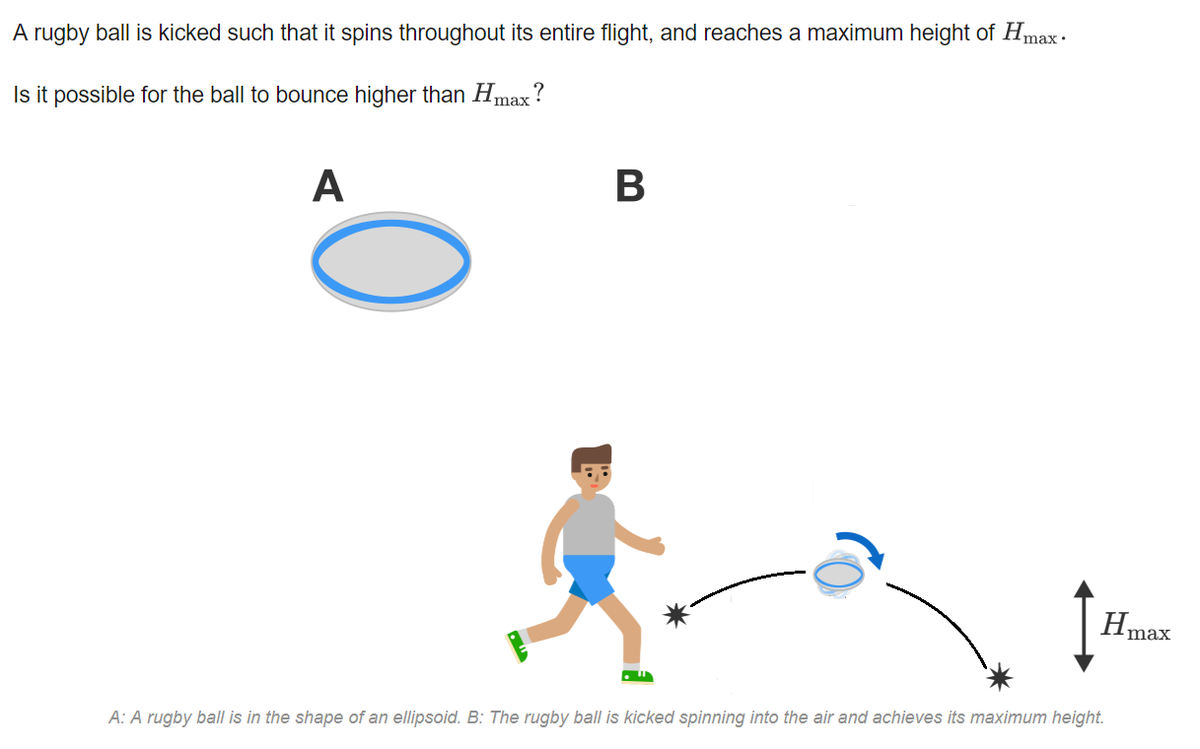
A rugby ball is kicked such that it spins throughout its entire flight, and reaches a maximum height of H max .
Is it possible for the ball to bounce higher than H max ?
A: A rugby ball is in the shape of an ellipsoid. B: The rugby ball is kicked spinning into the air and achieves its maximum height.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Just to clarify: are you saying that if the ball hits the ground correctly, the normal force will have to provide an angular impulse decreasing the angular momentum as well as the impulse to counteract the linear motion, so the total impulse provided by the normal force can be greater than that required to bounce up to H m a x ?
Log in to reply
In a rotating rugby ball, there are points which are moving at a speed greater than the speed of the center of mass. If the ball hits at a particular angle, impulse by the ground could be more than that required to bounce up to H max .
Log in to reply
Since "there are points which are moving at a speed greater than the speed of the center of mass" is true of every rotating object, I'm not sure how it can explain anything. For instance, it would be true of a spherical ball, but as I understand it a spinning spherical ball can only change rotational motion into linear motion parallel to the surface it impacts (via friction).
Log in to reply
@Brian Moehring – We are only concerned with the vertical component of the velocity of the point of impact of the rugby ball.
In a spherical ball, the point at which the ball collides with the ground has a vertical velocity equal to the velocity of its center of mass. Whereas in a rugby ball, the point of impact may have the vertical velocity greater than the velocity of the center of mass and hence may bounce higher.
Log in to reply
@Rohit Gupta – Thank you very much for the picture - that clarified it.
Log in to reply
@Brian Moehring – Am I right in thinking that Hmax must be very low in order for Vcm to be lower than V? I can't imagine the rugby ball rotating quickly enough to overcome a high initial velocity.
Log in to reply
@Brian Egedy – Not really. First note that we don't need fast rotation to have V c m < V . In fact, if we have a very slow rotation, then we would have V c m < V about half the time for very large H m a x .
Absent air resistance and assuming the kicker can precisely impart any linear and angular momenta he chooses, then there is no limit to H m a x .
With air resistance, the analysis becomes much more complicated, but I think it actually becomes easier for V c m < V for greater H m a x (at least with front-spin). The problem, of course, is that the air resistance would decrease both the linear and rotational kinetic energies throughout the flight, it could never bounce back to H m a x for large values of H m a x .
That being said, if we're only interested in the resulting bounce going above H m a x , it will happen much more often with smaller H m a x and smaller angles the rugby ball's path makes with the ground.
@Rohit Gupta – I think this deserves to be a separate answer so that it can be more easily seen.
As an aside, a spinning spherical ball can bounce higher, but only if it impacts on uneven ground, for example the edge of a wall. But again the same reasoning applies: the point which hits the wall has a vertical velocity bigger that that of the center of mass.
I personally prefer to think in limiting cases. A spherical ball rolling on the street (max height 0) can jump up if it hits a small object, thus attaining a higher maximal height than before it bounced. Similarly a rugby ball spinning at very small height is very likely to reach a higher height if it bounces. There will be almost no vertical speed, except locally at the point of impact.
Thanks for posting the beautiful video clincher. Any sceptics should keep watching to see the final take from the front!
There‘s a second video about this topic and when I saw the task it immediately reminded me of it. :) https://youtu.be/x4ySPDvebes
Log in to reply
I thought of that one as well - Dianna does great videos!
Thank you. But it is blocked in France :'( for TF1 copyright reasons.
Log in to reply
Salut, regarde celle-là si tu veux : https://www.youtube.com/watch?v=xbTQl9xBlII
No goal keeper?
Just being pedantic here but doesn't Hmax mean maximum height? If it's the highest point then anything that goes higher afterwards negates the fact it was "maximum"?
Log in to reply
H m a x is defined to be the maximum height the the ball reaches after it is kicked and before it bounces on the ground the first time. After the ball bounces, it may go higher than H m a x , with no semantic contradiction.
surely the video example only works because the player kicks the ball forwards. your diagram suggests the ball is only kicked upwards
Log in to reply
It's possible that the video actually shows a roll on the back end (converting horizontal momentum to angular momentum) followed by a bounce on the front end (converting angular momentum to vertical momentum). In that sense, it could be a "cheat", but the principle for the bounce applies all the same if the ball were kicked upwards.
Log in to reply
the video shows conversion of forward momentum into vertical momentum. The ball "sits up" for Barrett, i.e. its forward speed suddenly reduces, and is converted to vertical energy, little or nothing to do with rotational energy.
Log in to reply
@Nigel Morris – Besides, who wants to see Kiwis getting lucky again.
@Nigel Morris – The only way to have a direct conversion of horizontal momentum to vertical momentum without an intermediate or incidental change to angular momentum is to have an impulse act on the center of mass at an angle, or in normal terms, it would have to bounce flat against a sloped ground. Based on the amount of "pop" we see in the ball, it would seem there is a slope of about 3 0 ∘ in the field. Is that likely?
On the other hand, an intermediate change to angular momentum explains how the ball can slow its horizontal speed and then pop up, even on level ground.
Absolutely right Andrew Seed, in the (cool) video the ball has lots of forward motion, which is not the situation in the question.
H with the index "Max" - meaning the maximal height. Either formulate it other than "max" or it's wrong!
Once you start talking about the reatively low level energy involved in the rotation of a rugby ball you need to take into account air resistance, both to the vertical velocity and the rotational velocity(or specify in the question that air resistance is neglected). My guess is that air resistance, plus friction in deformation of the ball when it lands (unless you specified that away in the question as well), will more than outweigh any additional height that might be reached because of the rotational energy being converted into vertical travel energy. Also, unless the ball strikes at the correct angle, which will be an angle less than 90 to the ground and depend on the ball's shape, pressure, speed of rotation etc, the rotational energy will not all be converted and the ball will still rotate so less of the rotational energy will be converted to vertical energy. If the ball strikes at an angle less than 90 then the resulting force pushing back from the ground will not be vertical. and the ball will travel at an angle away from the ground, whereas it travelled vertically from the foot, so the height it reaches is quite likely to be less than the highest point that it reached when being kicked upwards.
Log in to reply
Nigel you would also need to specify no additional external forces apply. As it stands it could be bouncing on a rising platform which would impart an additional upward force rendering it trivial to identify a possibility that a bounce could exceed the height of the initial kick even with no net change of angular momentum. Also note the question is "is it possible" not "Will it" so as long as there is any possibility, irrespective of its likelihood the the answer must be yes.
Awesome video. And the physics is cool, too.
And the video... A+
Wrong. It can go higher than the first bouce, neve higher than Hmax.
Log in to reply
Fairly certain that Hmax refers to the apex of the initial kick, not the physical maximum altitude of the ball.
Miguel, that depends on the definition of "flight". If we assume that is defined as the motion between the initial kick and the first bounce then it is possible. I would agree that assumptions should be specified however.
Isn’t F=F? Force equal force? Why is it that the force outputed became larger?
Poorly formulated problem. Any answer would be a guess as to the author's assumptions. The ball could be spinning on a vertical axis... is air resistance negligible?... is thermodynamics at play?... which point of the ball is considered "the ball"? In addition, you state that angular momentum can be converted to linear momentum in a way such that the ball can be propelled upward - please do provide (even if informal) proof for such statements, especially with respect to what you treat as the "ball". I'd say with careful recasting, this problem can be transformed from confusing and vague to interesting and challenging.
Log in to reply
Agree completely, but the problem was very poorly worded.
I think I've figured out my initial confusion. Maybe this will help someone else.
Imagine the ball being kicked nearly horizontally, with very high velocity, but a very low Hmax. I believe this meets the parameters of the problem, as stated.
Because of the low launch angle, it loses very little horizontal velocity as it descends, and it happens to strike the earth on one of its ends, which redirects the bounce nearly vertically. The high velocity transferred from lateral to vertical force would cause the first bounce to be higher than Hmax.
Now gradually adjust the launch angle, and visualize the range in which these conditions could be met with progressively higher Hmax.
The redirection of the bounce angle makes more sense to me than the idea that the rotational momentum itself is what caused the change in bounce height.
Log in to reply
Agreed - and that's what I get from the video (and having chased a rugby ball in my school years). Most of the energy in the high bounce comes from horizontal motion being reflected into vertical; the rotation is not the primary energy reserve.
However in theory the problem as described could result in a higher bounce purely from rotational energy, in practice the rotational kinetic energy alone is too small to translate into significant vertical motion. Perhaps if the ball was kicked in a way that gave it very high RPM but almost no horizontal or vertical motion (maybe it travels only 1 metre before bouncing) then, maybe, I'd expect it could cause a high bounce.
Mythbusters time!
Log in to reply
The only reasonable method of changing horizontal motion directly to vertical motion is to bounce the rugby ball against a [locally] sloped surface. On a flat surface, especially one with grass, there are methods for horizontal motion to be changed into rotational and then rotational into vertical. Assuming you haven't been playing on a very uneven field, this is much more likely what you've seen.
Log in to reply
@Brian Moehring – I would expect that to be true for a soccer ball, but there's something else happening with the way a fast moving (horizontally) rugby ball bounces.
Watch the Beauden Barrett try frame by frame. Just after the 22 metre line he kicks it forward, the ball is moving away from him (faster than him), then it bounces and rears up; at that point it starts spinning fast and its horizontal motion is slowed down.
What appears to be happening there is that the energy has come from the horizontal motion, and because of the oval shape of the ball if ti lands on flattest side then it will lever itself skywards and take on some spin at the same time.
Imagine a rugby ball travelling at speed with absolutely no end-over-end spin, with the long axis parallel to the ground. Then consider what will happen when that makes contact with the ground and starts to rotate. When the rotation reaches the sharp end the center of gravity will be lifted, friction will bite harder, and you will end up with a ball spinning,with reduced horizontal speed and increased vertical.
Log in to reply
@Jamie Clark – A soccer ball satisfies everything I mentioned in my post except the ability to change rotational motion into vertical motion, which is the key step a rugby ball allows.
We seem to be agreeing on the final result as well as the fact that the kicker gives more horizontal linear energy to the ball than he does rotational energy, but you had seemingly implied that the horizontal motion can directly change into a vertical motion on a flat surface, and this is simply not true. The exact difference between a soccer ball and a rugby ball is that the change between horizontal and rotational motion (which can happen with both) can then be changed to vertical motion in a rubgy ball, but only in the steps horizontal friction rotational normal impulse vertical
Am I right in thinking we agree here? That is, there is no direct change from horizontal to vertical motion?
Log in to reply
@Brian Moehring – More or less, yes that's what I'm implying. Although I'd suggest the rotational output is incidental or occurs at the same time as the vertical. There is no intermediate step where the ball spins and then starts accelerating vertically while losing rotational energy, but I'll accept that rotation is involved in lifting the COG of the ball.
But in any case this is quite a different explanation than the original post which suggested the source of the increase height was rotational kinetic energy that the ball possessed before the bounce. The video illustrates that the energy source of the high bounce is linear kinetic.
Immediately before ground contact: ball is traveling fast horizontally, with imperceptible rotation. Immediately after ground contact: ball is traveling slower horizontally, faster vertically, and also with greater rotational energy.
Log in to reply
@Jamie Clark – Oh, I didn't look as close at the video as you did obviously, but I had my suspicions that that was actually what was happening.
In a previous thread, I actually implied that this type of phenomenon where the ball "pops" up like that is more likely to happen for precisely this reason. However, if we believe the immediate source of the vertical motion is from rotational motion, then it will still be possible to do this with no initial horizontal motion, at least in the ideal case of a perfectly elastic collision and no air resistance.
Log in to reply
@Brian Moehring – I believe so too, and answered the original mechanics question in the affirmative. However that was thinking in simple terms and suspending the practical details (the physics of the kick, for example).
Quite an interesting topic though - reminds me of those (long since forgotten in this case) experiments with rolling cylinders, spheres, and the relative translational / rotational energies.
@Andrew Hayes , Sir your video isn't working, btw I don't know why I came to this problem again after so many months lol
Similarly to how a tic-tac can bounce higher than the original height from which it is dropped by converting its rotational energy to kinetic energy, a rugby ball can do the same thing. This video by Physics Girl, perfectly explains it.
H with the index "Max" - meaning the maximal height. Either formulate it other than "max" or it's wrong!
Log in to reply
it is a local maximum as described to be heighest from kick to first bounce. learn to read descriptions before telling somebody is wrong
Wrong. It can go higher than the first bouce, neve higher than Hmax.
First in question..... Ball has two type of energy, I.e. kintic and rotational... (keeping in mind the shape of the ball)... The rotation of the ball takes energy to rotate, due to friction.... If the ball kicked at a certain point,( as possible 90 Degree) that is ball doesn't rotate at all...( The Ball will use energy for kinetic motion Not for rotation)) This can take ball to higher than the previous one....😊
May be I don't understand problem, but in the video the kinetic energy (bal) has a horizontal part that is converter by rotation in vertical direction. The sketch is not so proper, I think that the ball is kicked in vertical direction and hit in back way a ground and in this case it will not bounce higher than H max. This is a borderline case, in higher ramp way the solution will be "No"
Don’t understand why people are taking about a bounce. In the diagram there is no bounce. Surely this is to do with the fact that top spin can give lift so if it is given more spin it can go higher.
This question is entirely deficient and lacking in proper structure and is entirely inappropriate to Brilliant.Org and an insult to its community.
Then what are you waiting for? Go ahead and report it. What is stopping you from it ?????
The salt is strong with this one
And yh, I was confused about the "maximum height it spoke about . So I thought it was impossible to travel higher however Where as the ball spins instead of just travels directly upwards because of how he kicked it . It can bounce higher because of how it can bounce on the ground .
Assuming a coefficient of restitution of 1, the ball can bounce as high as it was dropped. Let's just use the conservation of energy equation as well as the conservation of momentum equation. Many possible ways to show this.
While I answered yes, if we're really dealing with a rugby ball kicked on Earth, the answer is no, because wind resistance, plasticity in the ground and plasticity in the ball will have a greater effect than converting a bit of the rotational kinetic energy.
Update: though I admit that my answer was influenced by the image showing a high angle in the kick, not merely skimming along the ground where the effect is much easier to achieve.
Rugby balls are rarely if ever kicked straight up, either having to simply cross the 22, or reach the 10 at a kick-off, usually with a significant component across the field of play, but the time spin is deliberately added from a kick is - as with passing - to keep the ball from tumbling uncontrollably, much as with the rifling of a gun barrel to make a bullet spin. See also https://en.wikipedia.org/wiki/Spin-stabilisation.
Figure B is misleading; the information in Figure A alone is sufficient to explain the irregular bounce. See https://projecteuler.net/problem=144 for another bouncing ellipse.
With a question such as this, the more realistic scenario as illustrated below makes it much too easy to answer correctly. The ball has potential energy, a scalar quantity, as well as three components of a vector of kinetic energy, and indeed angular kinetic energy too.
Bonus: if a rugby ball is spun in place on the ground (as in https://www.youtube.com/watch?v=eftQ71uTTVI), then even if it is initially on its side, that is to say with its centre of gravity some 9-10 cm above the ground, then the little bounces on the ground it loses energy from will cause it to raise its centre of gravity by some 5cm as it spins on one of the pointed ends. Google tells me that "435g * g * 5cm in joules" is about 0.22 J, and of course conservation of angular momentum also plays a part in this.
good explanation https://www.youtube.com/watch?v=x4ySPDvebes
Just like an onside kick in American Football. An end-over-end rolling/bouncing football can suddenly bounce much higher than previous bounce...
Right before the ball bounces, it has both rotational and translational kinetic energy. Due to the ball's shape, some of that rotational energy is converted into translational energy as the ball bounces. If the ball bounces at a certain angle, this converted energy can take the ball to a higher height than its previous height.
This effect can be seen in this video .