Bouncing off of the Sides of A Triangle Forever

Geometry Level 5

Let $ABC$ be a triangle such that $BC=5$ , $CA=8$ , and $AB=9$ . A ball is launched from a point $X$ on segment $BC$ such that it first bounces off of segment $CA$ at a point $Y$ , then bounces off of segment $AB$ at a point $Z$ , then bounces off of segment $BC$ at $X$ , then bounces off of segment $CA$ at $Y$ , and so on, traversing the perimeter of triangle $XYZ$ forever.

The area of triangle $XYZ$ can be written in the form $\tfrac{p\sqrt{q}}{r}$ , where $p$ and $r$ are coprime positive integers and $q$ is a squarefree integer. Find $p+q+r$ .

The answer is 33.

3 solutions

Hugh Sir
Aug 8, 2014

The triangle XYZ is call the 'orthic triangle', which is formed by the feet of the three altitudes of the triangle ABC.

The lengths of the sides of the orthic triangle are:

$x = a \cos(A)$

$y= b \cos(B)$

$z = c \cos(C)$

Applying the cosine rule, we have

$x = 5 \cos(A) = 5 (\frac{8^{2}+9^{2}-5^{2}}{2(8)(9)}) = \frac{25}{6}$

$y = 8 \cos(B) = 8 (\frac{9^{2}+5^{2}-8^{2}}{2(9)(5)}) = \frac{56}{15}$

$z = 9 \cos(C) = 9 (\frac{5^{2}+8^{2}-9^{2}}{2(5)(8)}) = \frac{9}{10}$

The area of the triangle XYZ, thus, can be found by applying the Heron's formula.

$s = \frac{x+y+z}{2} = \frac{22}{5}$

$Area = \sqrt{s(s-x)(s-y)(s-z)} = \frac{7\sqrt{11}}{15}$

Hence,

$p+q+r = 7+11+15 = 33$

Why the triangle XYZ is formed by the feet of the three altitudes of the triangle ABC? How did you know this?

Enoc Cetina - 6 years, 10 months ago

Each altitude of triangle ABC is the normal line that divides the angle between the incident path and the reflected path of the ball into two equal angles. In order to make the ball bounces off the three sides of the triangle forever, the path of the ball must go from each feet of the three altitudes.

Hugh Sir - 6 years, 10 months ago

Not quite. Your argument merely shows that "If we start off at the foot of the perpendicular, and project the ball towards the other foot, then we will get a periodic path".

Enoc is asking: "Why is that the only possible triangle"? That is a good question to ask.

Calvin Lin Staff - 6 years, 10 months ago

@Calvin Lin – Here's the "almost completed" proof that there're no other triangles possible. I don't have much time for this right now, too much homework at school XP, so you can continue this proof if you want to.

Draw another triangle $X'Y'Z'$ pretend to be different to $XYZ$ such that $Z'\hat{X'}A = A\hat{X'}Y, X'\hat{Y'}B = B\hat{Y'}Z, Y'\hat{Z'}C = C\hat{Z'}X$

Since the angles are equal, the 3 lines $\overline{AX'}, \overline{BY'}, \overline{CZ'}$ must intersect at the incenter of $\Delta XYZ$ , call it $I$ .

Since $\overline{AX'} \not\perp \overline{BC}, \overline{BY'} \not\perp \overline{CA}, \overline{CZ'} \not\perp \overline{AB}$ , we give that $\square AY'IZ', \square BZ'IX', \square CX'IY'$ are not cyclic, which also leads that $\square BZ'Y'C, \square CX'Z'A, \square AY'X'B$ not cyclic.

Because these 6 equations

$I\hat{Y}A + I\hat{Z}A = 180^{\circ}, I\hat{Z}A + I\hat{Z}B = 180^{\circ}, I\hat{Z}B + I\hat{X}B = 180^{\circ}, I\hat{X}B + I\hat{X}C = 180^{\circ}, I\hat{X}C + I\hat{Y}C = 180^{\circ}, I\hat{Y}C + I\hat{Y}A = 180^{\circ}$

can only have 1 solution of each angle is 90 degrees.

Consider $\square BZ'IX'$ , since it's not cyclic, we have $I\hat{X'}Z' \neq I\hat{B}Z', B\hat{Z'}X' \neq B\hat{I}Z'$ .

Samuraiwarm Tsunayoshi - 6 years, 10 months ago

I can't believe I wasted two tries accidentally thinking that the sides were $5$ , $7$ , and $8$ ... And then I get it wrong from calc mistake.

Daniel Liu - 6 years, 10 months ago

Ujjwal Rane
Oct 31, 2014

Imgur Imgur

Labeling angles as shown in the top figure, we can apply 'sum of angles of a triangle = 180' to get $\phi = 180 - \theta - \alpha; \psi = \theta + \alpha - \beta; \theta = 180 - \gamma -\theta - \alpha + \beta$ Yielding $\theta = \beta; \phi = \gamma; \psi = \alpha$ Thus around the path there are three triangles similar to the original! Let ZB = 5x, then we can go around the triangle writing lengths in terms of x as shown in the bottom figure

AY + YC = 8 gives x = 7/15

and ZX = 56/15; XY = 9/10; YZ = 25/6

Finally, using Heron's formula for area with semiperimeter = 22/5; we get the area - $A = \sqrt{\frac{22}{5} \frac{7}{2} \frac{2}{3} \frac{7}{30}} = \frac {7 \sqrt{11}}{15}$

Beautiful, short, simple solution, directly from basics. Yes as it is normal with you.+1).

Niranjan Khanderia - 4 years, 2 months ago

Thank you sir!

Ujjwal Rane - 4 years, 1 month ago

Niranjan Khanderia
Apr 11, 2017

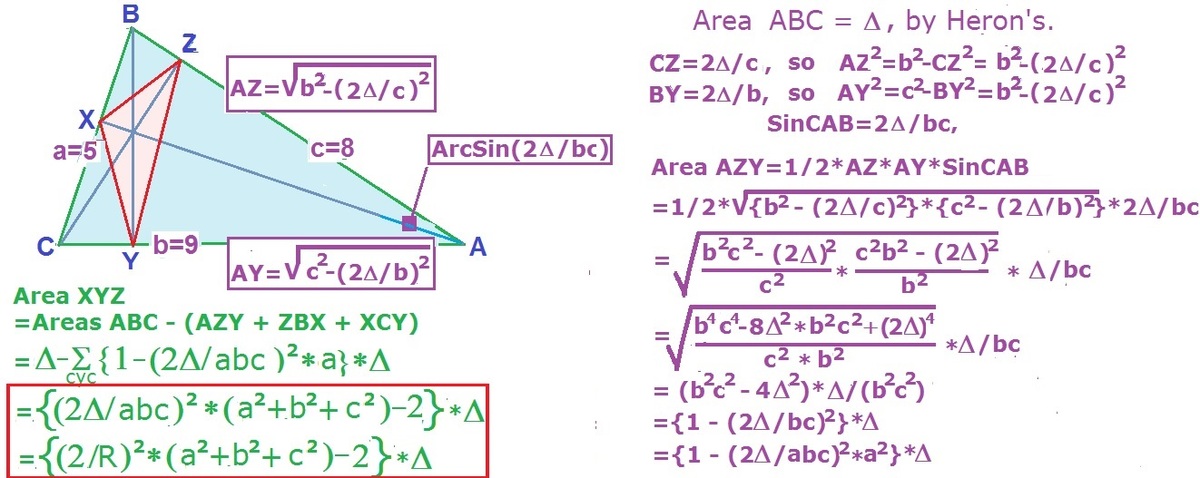
Bouncing off of the Sides of A Triangle Forever is possible if the path followed is Orthic triangle. So below we find the area of Orthic triangle of given ABC. The general formula I have developed in terms a, b, c is:-(Area of the original triangle can be found through Heron's)

$\color{#D61F06}{Area ~of~ Orthic~ triangle =\Bigg( ~~\bigg( \dfrac{2*area ~original~ triangle}{abc} \bigg)^2*(a^2+b^2+c^2)- 2 \Bigg)*(area ~original~ triangle)}\\$

$Area ~of~ Orthic~ triangle =\Bigg( \bigg(\dfrac{2*6*\sqrt{11}}{5*8*9}\bigg)^2*( 25+64+81) -2\Bigg)*(6*\sqrt{11})=\bigg(\dfrac{187}{90}-2 \bigg)*(6*\sqrt{11})\\ Area ~of~ Orthic~ triangle = \dfrac 7 {90} *6*\sqrt{11}= \dfrac 7 {15}*\sqrt{11}.\\ p+q+r=7+11+15=33.$

Bouncing off of the Sides of A Triangle Forever

The answer is 33.

3 solutions

0 pending reports